Гамма-алгоритм (в общем виде) 3 страница

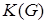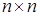Определение. Матрицей Кирхгофа простого графа называется -матрица с элементами, которые определяются так:

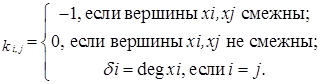
Сумма элементов в каждой строке и каждом столбце матрицы 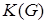равна нулю.

Теорема Кирхгофа. Число остовных деревьев в простом связном графе с вершинами равно алгебраическому дополнению любого элемента матрицы Кирхгофа .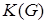

21.6 Алгоритмы построения остовов графа

Задача отыскания кратчайшего остова графа является классической задачей теории графов. Методы решения этой задачи послужили основой для многих других важных результатов. Задача о нахождении кратчайшего остова принадлежит к числу немногих задач теории графов, которые можно считать полностью решенными. Между тем, если изменить условия задачи, на первый взгляд даже незначительно, то она оказывается значительно более трудной.

Алгоритм строит остов:

Вход: граф 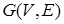, заданный матрицей длин рёбер .

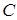Выход: остов .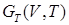

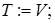
while в больше одного элемента do

взять любое поддерево из

найти к нему ближайшее

соединить эти деревья в

end while

В частности, исследования алгоритма Краскала привели в конечном счете к теории жадных алгоритмов. Следующий жадный алгоритм, известный как алгоритм Краскала, находит кратчайший остов в связном графе.

Алгоритм Краскала

Вход: список 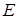рёбер графа с длинами. .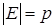

Выход: множество рёбер кратчайшего остова.

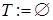
Упорядочить 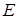в порядке возрастания длин

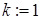{ номер рассматриваемого ребра }

for from 1 t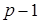o do

while добавление ребра 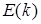образует цикл в do

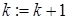{пропустить ребро }

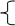end while

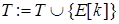{добавить это ребро в SST }

end for

(SST-Shortest Sceleton Tree - стандартное обозначение для кратчайшего остова).

Пример. Дан нагруженный граф . Необходимо построить минимальное остовное дерево .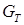

Алгоритм: Строим таблицу, в которую заносим все ребра с их стоимостями в порядке возрастания. На каждом шаге алгоритма включаем в остовное дерево ребро графа минимальной стоимости, проверяя, не образуется ли цикл с уже включенными в дерево ребрами.

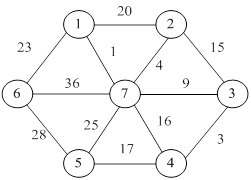
Рисунок 21.8

Рисунки 21.9 – 21.11 иллюстрируют работу алгоритма Краскала.

Шаг	Ребро	Стоимость	+/-
	(1, 7)		включаем
	(3, 4)		включаем
	(2, 7)		включаем
	(3, 7)		включаем
	(2, 3)		образует цикл, не включаем
	(4, 7)		образует цикл, не включаем
	(1, 5)		включаем
	(1, 2)		образует цикл, не включаем
	(1, 6)		Включаем. Все вершины включены в остов. Конец.
	(5, 7)
	(5, 6)
	(6, 7)

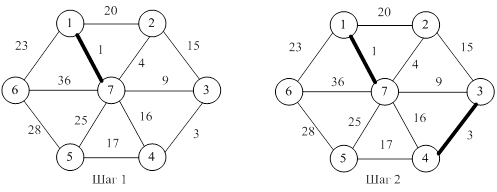
Рисунок 21.9

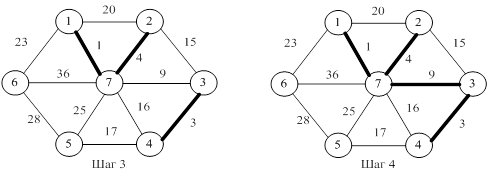
Рисунок 21.10

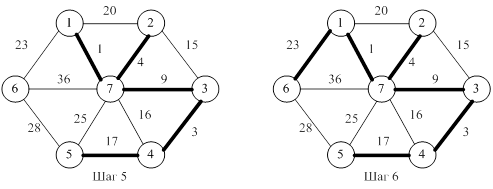
Рисунок 21.11

В результате работы алгоритма получаем остов минимальной стоимости: 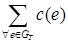=57.

21.7 Ориентированные и бинарные деревья. Определения

Ориентированное дерево (корневое ориентированное дерево) (рис. 21.12) – это ориентированный граф без циклов со свойствами:

1. Существует в точности одна вершина 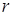, называемая корнем, в которую не заходит ни одна дуга.

2. В каждую вершину, кроме корня, заходит в точности одна дуга.

3. Существует путь из корня в любую другую вершину.

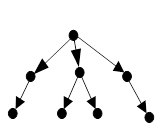
Рисунок 21.12

Потомок вершины – это вершина , в которую ведет путь из вершины ; при этом называется предком для . Если длина этого пути равна 1, то есть из в ведет дуга, то – «отец» для , а – «сын» для .

Вершины, у которых общий отец, называются братьями или сестрами.

Вершина, не имеющая потомков, называется листом.

Глубина вершины в дереве – это длина пути из корня в .

Высота вершины в дереве – это длина самого длинного пути из в какой-нибудь лист.

Высота дерева – это число дуг самого длинного пути, то есть высота корня.

Уровень вершины – это разность между высотой всего дерева и глубиной вершины .

Высота дерева на рис. 21.13 равна 3, вершина 8 имеет глубину 2, высоту 1, уровень 1.

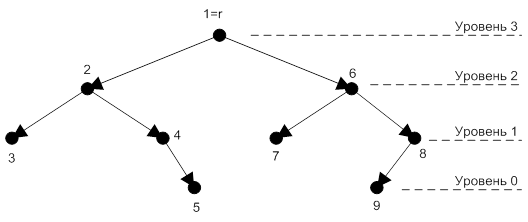
Рисунок 21.13

Лемма. Если в любом неориентированном дереве 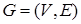выбрать произвольную вершину 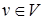в качестве корня и сориентировать все ребра в направлении «от корня», т.е. сделать началом всех инцидентных ей ребер, вершины, смежные с – началами всех инцидентных им еще не сориентированных ребер и т.д., то полученный в результате ориентированный граф 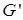будет ориентированным деревом.

Упорядоченное ориентированное дерево – это дерево, у которого множество сыновей каждой вершины упорядочено, обычно слева направо, как на рисунке 62: .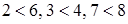

Бинарное (двоичное) дерево – это упорядоченное дерево, из каждой вершины которого может исходить не более двух дуг. Ориентированное дерево называют бинарным, если полустепень исхода любой его вершины не больше 2.

Бинарное ориентированное дерево называют полным, если из любой его вершины, не являющейся листом, исходят ровно две дуги, а уровни всех листьев совпадают.

Каждая вершина бинарного дерева может иметь либо двух сыновей – левого и правого (вершина 2 имеет левого сына 3 и правого сына 4), либо иметь только левого сына (левый сын 9 вершины 8), либо только правого сына (вершина 5 – единственный правый сын вершины 4), либо не иметь ни одного сына (листья 3, 5, 7, 9).

Бинарное дерево называется полным, если у каждой его внутренней вершины имеется два сына и все его ветви имеют одинаковую длину.

Полное бинарное дерево уровня – это дерево, в котором каждый узел уровня является листом и каждый узел уровня меньше имеет непустые левое и правое поддеревья.

На рис. 21.14 приведен пример полного бинарного дерева уровня 3.

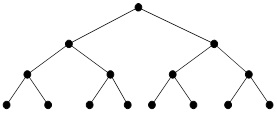
Рисунок 21.14

Левое поддерево вершины – это максимальное поддерево, корнем которого является левый сын 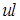вершины .

Правое поддерево вершины – это максимальное поддерево, корнем которого является правый сын 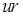вершины .

На рисунке 6.77 левое поддерево вершины 6 состоит из одной вершины 7, правое поддерево – из вершин 8, 9 и дуги (8,9).

Теорема 21.5 (теорема о высоте бинарного ориентированного дерева с заданным числом листьев). Бинарное ориентированное дерево с листьями имеет высоту, не меньшую .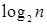

21.8 Правила прохождения бинарных деревьев

Над бинарным деревом есть операция – его прохождение, т.е. нужно обойти все дерево, отметив каждый узел один раз.

Существует 3 способа обхода бинарного дерева:

1. В прямом порядке.

2. В симметричном порядке.

3. В обратном порядке.

В прямом порядке (обход в прямом порядке, прямой обход, упорядоченный обход, обход сверху, обход в ширину, preorder):

1. Попасть в корень.

2. Пройти в прямом порядке левое поддерево.

3. Пройти в прямом порядке правое поддерево.

В симметричном порядке (обход симметричным способом, симметричный обход, inorder):

1. Пройти в симметричном порядке левое поддерево.

2. Попасть в корень.

3. Пройти в симметричном порядке правое поддерево.

В обратном порядке (обход в обратном порядке, обход в глубину, обратный обход, обход снизу, postorder):

1. Пройти в обратном порядке левое поддерево.

2. Пройти в обратном порядке правое поддерево.

3. Попасть в корень.

21.9 Эквивалентные бинарные деревья

Дерево и лес любого вида можно преобразовать единственным образом в эквивалентное бинарное дерево.

Правило построения бинарного дерева из любого дерева:

1. В каждом узле оставить только ветвь к старшему сыну (вертикальное соединение).

2. Соединить горизонтальными ребрами всех братьев одного отца.

3. Таким образом перестроить дерево по правилу:

– левый сын – вершина, расположенная под данной вершиной;

– правый сын – вершина, расположенная справа от данной вершины(т.е. на одном ярусе с ней).

4. Развернуть дерево таким образом, чтобы все вертикальные ветви отображали левых сыновей, а горизонтальные – правых.

В результате преобразования любого дерева в бинарное получается дерево в виде левого поддерева, подвешенного к корневой вершине.

Описанный выше метод представления произвольных упорядоченных деревьев посредством бинарных деревьев можно обобщить на представление произвольного упорядоченного леса.

Правило построения бинарного дерева из леса: корни всех поддеревьев леса соединить горизонтальными связями. В полученном дереве узлы в данном примере будут располагаться на трех уровнях. Далее перестраивать по ранее рассмотренному плану. В результате преобразования упорядоченного леса в бинарное дерево получается полное бинарное дерево с левым и правым поддеревом.

21.10 Контрольные вопросы и задания

1. Какой граф называется деревом. Приведите примеры деревьев.

2. Что называется лесом в теории графов?

3. Перечислите основные свойства деревьев.

4. Какой формулой можно воспользоваться для определения количества неориентированных помеченных графов?

5. Какой формулой можно воспользоваться для определения количества неориентированных помеченных деревьев?

6. Как определить число неизоморфных графов без пометок?

7. В каких случаях используется формула А. Кэли? Приведите эту формулу.

8. Дайте определения основа (каркаса) графа.

9. Приведите пример составления матрицы Кирхгофа простого графа.

10. Для решения каких задач используется теорема Кирхгофа.

11. Перечислите основные алгоритмы построения остовов графа.

12. Приведите алгоритм Краскала для построения остова графа.

13. Дайте определение ориентированных и бинарных деревьев.

14. Охарактеризуйте способы обхода бинарного дерева.

Лекция 22. Цикломатика графов. Раскраска графов

22.1 Цикломатика графов

22.1.1 Определения цикломатики графов

Маршрут (соединяющий вершины 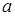и 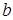) – это конечная последовательность ребер и инцидентных им вершин, составляющих непрерывную кривую с концам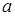и и 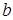. Число ребер в маршруте называется его длиной.

Маршрут замкнут, если концы его совпадают ( ).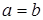

Маршрут, в котором все рёбра попарно различны, называется цепью.

Маршрут, в котором все вершины попарно различны, называется простой цепью.

Цикл – это замкнутая цепь.

Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

Для ориентированных графов цепь называется путем, а цикл – контуром.

Пример. В графе на рис. 22.1: 1. 1, 3, 1, 4 – маршрут, но не цепь; 2. 1, 3, 5, 2, 3, 4 – цепь, но не простая цепь; 3. 1, 4, 3, 2, 5 – простая цепь; 4. 1, 3, 5, 2, 3, 4, 1 – цикл, но не простой цикл; 5. 1, 3, 4, 1 – простой цикл.

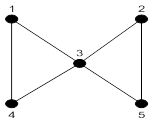
Рисунок 22.1

Граф называется ациклическим, если он не содержит циклов (рис. 22.2).

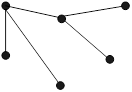
Рисунок 22.2– Ациклический граф (дерево)

Следующие три определения равнозначны:

Каркас (остов) – это максимальный подграф без циклов.

Остов графа – ациклический подграф исходного графа, полученный путем удаления из исходного графа ребер так, чтобы не изменилось количество компонент связанности.

Остовный подграф графа – это подграф, содержащий все вершины графа.

Пример.На рис. 22.3 жирными линиями выделены ребра остова.

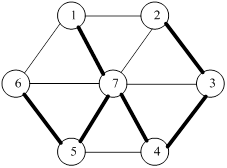
Рисунок 22.3– Остов и кодерево

Деревомназывается связный граф, не содержащий ни одного цикла.

Хордой остова 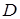в связном графе называется всякое ребро графа, не принадлежащее 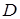. Любой подграф, который состоит из хорды и остова, имеет точно один цикл.

Кодерево графа – такой подграф графа, который содержит все его вершины и те ребра, которые не вошли в остов.

Пример.На рис. 22.3 полужирными линиями выделены ребра остова, тонкими линиями – ребра кодерева.

22.1.2 Цикломатическое число и его свойства

Определение.Наименьшее число 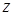, показывающее, сколько ребер необходимо удалить из графа, чтобы получить его остов, называется цикломатическим числом. 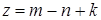, то есть, чтобы найти цикломатическое число графа, необходимо из числа ребер вычесть число вершин и к результату прибавить число компонент.

В случае связного графа 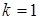, следовательно, .

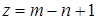Пример. Для графа, приведенного на рис. 22.4, ; .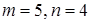

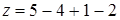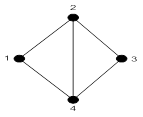
Рисунок 22.4

Цикломатическое число всегда неотрицательно.

Цикломатическое число остова графа равно нулю.

Основное свойство цикломатического числа формулируется в виде теоремы: цикломатическое число мультиграфа равно максимальному числу независимых циклов.

Цикломатическое число несвязного графа с компонентами связности 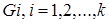может быть определено как сумма цикломатических чисел его компонент связности: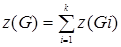

Определение.Совокупность циклов графа называется линейно-независимой по модулю 2, если ни один цикл из данной совокупности нельзя получить с помощью линейной комбинации по модулю 2 остальных циклов.

Цикломатическое число графа постоянно и равно числу линейно-независимых циклов графа.

22.1.3 Цикломатическая матрица

Определение. 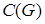– цикломатическая матрица графа – это матрица, столбцам которой соответствуют ребра графа, а строки соответствуют циклам. 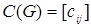. Каждый элемент этой строки определяется следующим образом:

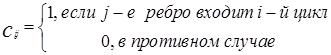
Каждому циклу графа взаимно однозначно сопоставляется вектор-строка матрицы .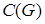

Цикломатическая матрица не задает граф с точностью до изоморфизма.

22.1.4 Базис циклов

Определение.Множество 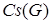всех векторов, каждый из которых соответствует одному циклу графа , образует векторное пространство, называемое пространством циклов графа . При этом для любых двух циклов 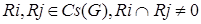существует некоторый третий цикл 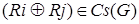, где символ 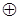обозначает поразрядное сложение по модулю два.

Определение. Базисом пространства цикловназывается всякая система линейно независимых векторов, порождающая данное пространство. Всякий элемент пространства циклов единственным образом представим в виде линейной комбинации векторов базиса пространства циклов. Если пространство имеет базис из векторов, то оно называется -мерным пространством.

Система циклов графа называется полной, если любой цикл данного графа представляется в виде линейной комбинации циклов из этой системы.

Базисом циклов графа называется любая полная линейно независимая система циклов данного графа. Базис циклов графа – это базис пространства циклов графа , состоящий из простых циклов. Любой вектор пространства циклов графа можно представить в виде линейной комбинации векторов базиса циклов.

Пример.Рассмотрим граф, изображенный на рис. 22.5.

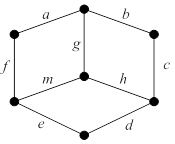
Рисунок 22.5

Цикломатическая матрица 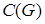этого графа имеет вид:

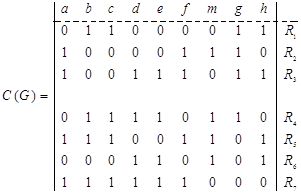
В качестве базиса циклов можно взять множество циклов 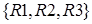. Можно убедиться в том, что все остальные циклы выражаются их линейными комбинациями: .

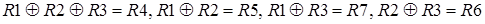Определение. Сечение графа – это множество рёбер, удаление которых делит граф на два изолированных подграфа,

Сечение 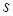называется фундаментальным (по дереву ), если оно содержит в точности одну дугу 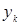дерева , а ориентация сечения 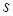согласована с ориентацией дуги .

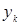Пример.На рис. 22.6 пунктирами показаны фундаментальные сечения 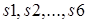по дереву «большая медведица».

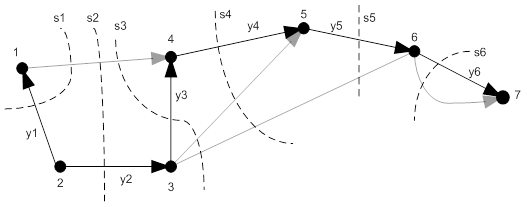
Рисунок 22.6