Закон исключенного третьего 6 страница

Теорема.

Если 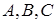− любые формулы, то имеют место следующие логические эквивалентности:

1. 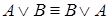, 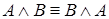(коммутативность).

2. 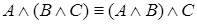, 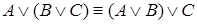(ассоциативность).

3. ,

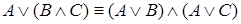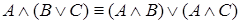(дистирибутивность).

4. 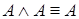, 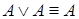(идемпотентность).

5. 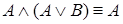, 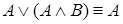(законы поглощения).

6. 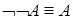(закон двойного отрицания.)

7. 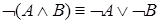, 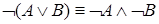(законы де Моргана).

8. , .

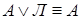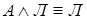9. , .

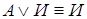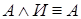10. , .

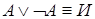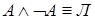Кроме того, с помощью отношения равносильности выражаются различные связки между формулами: , , , , , , .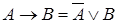

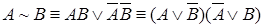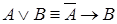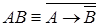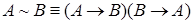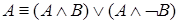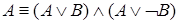Любая из равносильностей может быть доказана с помощью таблиц истинности (а также следует из изоморфизма алгебр 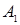и ).

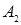Рассмотренные и подобные им равносильные соотношения можно использовать для преобразования и упрощения структуры сложного высказывания.

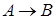Определение.Высказывание является логическим следствием высказывания , если формула является тождественно истинной.

Данное определение может быть обобщено на случай произвольного числа посылок.

Определение.Высказывание является логическим следствием высказываний 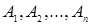, если 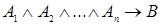− тождественно истинная формула.

Пример.Показать, что высказывание 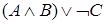является логическим следованием высказывания .

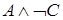Покажем, что формула 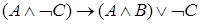является общезначимой. Для этого используем тождества логики высказываний для эквивалентных преобразований, учитывая, что :

.

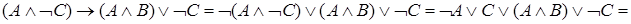
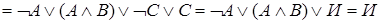Общезначимость формулы доказана.

10.6 Контрольные вопросы и задания

1. Какой вид предложений моделирует формальная логика?

2. Дайте определение понятию высказывание.

3. Дайте определение понятию алгебры логики высказываний.

4. Какие высказывания называются атомами?

5. Что в логике высказываний называют логическими связками?

6. Что в логике высказываний называют молекулами?

7. Дайте характеристику алфавита логики высказываний.

8. Что подразумевают в логике высказываний под правильно построенной формулой?

9. Дайте определение логического следствия одного (нескольких) высказываний.

10. Покажите, что алгебра логики и логика высказываний являются изоморфными.

11. Какие формулы можно получить, исходя из принимаемых формулами логики высказываний истинностных значений?

12. Какое рассуждение называется правильным?

13. Перечислите наиболее важные тавтологии.

14. Какие формулы называются равносильными? Приведите примеры равносильных формул.

Лекция 11. Исчисление высказываний

11.1 Основные понятия исчисления высказываний

Рассмотренное содержательное описание логики высказываний позволяет ответить на многие вопросы данной логики (например, является ли формула тавтологией, равносильны ли две заданные формулы и т.д.), используя таблицы истинности либо эквивалентные преобразования формул. Однако для ответа на более сложные вопросы используется другой метод − метод формальных аксиоматических теорий.

Исчисление высказываний, являясь формальной системой, представляет собой пример аксиоматической теории и один из возможных способов формализации логики высказываний. В исчислении высказываний особое внимание уделяется тождественно истинным высказываниям, поскольку они должны входить в любую теорию в качестве общелогических законов. Их порождение и является основной задачей исчисления высказываний. Данная формальная система позволяет проверить, является ли заданная формула тавтологией, а также получить общезначимые формулы логики высказываний.

Исчисление высказываний содержит язык, систему аксиом и правила вывода.

Рассмотрим каждое из этих составляющих.

Определение. Язык исчислениявысказываний, являясь формальным языком для математических рассуждений, состоит из формул логики высказываний, правильно построенных с использованием алфавита данной логики.

Пример.Правильно построенные формулы с использованием алфавита логики высказываний: 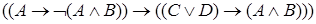, 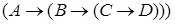. Выражения, не являющиеся формулами: , , .

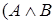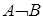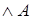11.2 Аксиомы и полнота исчисления логики высказываний

В математике и «чистой» логике доказывают теоремы, т.е. выводят следствия из определенных допущений, которые называются аксиомами или гипотезами. При этом предполагается, что они (аксиомы или гипотезы) тождественно истинны во всей рассматриваемой теории.

Определение.

Аксиомами логики высказываний является некоторое множество общезначимых формул логики высказываний.

Аксиомы (гипотезы) представляют собой перечень одного или более высказываний (посылок), которые часто называются схемами аксиом.

Системы аксиом исчисления высказываний подбираются таким образом, чтобы исчисление обладало свойством полноты.

Полнота исчисления высказываний заключается в том, что в данной системе имеется достаточное количество аксиом для того, чтобы вывести любую формулу логики высказываний, которая является тождественно истинной.

11.3 Выводимость в исчислении высказываний

Определение.

Выводом в исчислении высказывания называется всякая последовательность 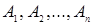формул такая, что для любого 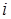формула 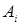есть либо аксиома, исчисления высказываний, либо непосредственное следствие каких-либо предыдущих формул, полученных по правилу вывода.

Определение.

Формула называется теоремой исчисления высказывания (как аксиоматической теории), если в ней существует вывод, в котором последней формулой является . Этот вывод называется выводом формулы .

Определение.

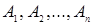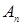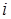Формула называется следствием множества формул тогда и только тогда, когда существует такая последовательность формул , что есть , и для любого формула 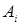есть либо аксиома, либо формула из , либо непосредственное следование некоторых предыдущих формул. Эта последовательность называется выводом из . Элементы называются посылками вывода или гипотезами.

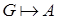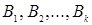Сокращенно можно записать так: ( есть следствие ). Если множество состоит из формул , то пишут .

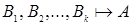Правила вывода позволяют получать новые формулы, которые являются истинными при условии истинности всех посылок, входящих в правило.

В логике правила вывода используются, чтобы выводить одни истинные предложения из других истинных предложений.

Доказательство в исчислении высказываний представляет собой логический вывод списка высказываний.

Определение.

Дедуктивным выводомназывается вывод формулы из формулы , основанный на том, что является логическим следствием .

Правила для дедуктивного вывода строятся на основе общезначимых формул логики высказываний вида 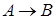. Эти правила часто записывают как правила формального вывода в следующем ви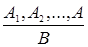де , где 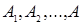- посылки вывода, а следствие (заключение). Тавтология, соответствующая такому правилу, - это .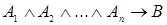

Пример.

Рассуждение по схеме 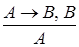не правильное рассуждение, так как формула 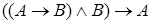не является тавтологией. Например, пусть : «5 − простое число» и : «5 − нечетное число», 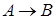: «Если 5 − простое число, то 5 − нечетное число» и : «5 − нечетное число», то : «5 − простое число», не правильное рассуждение.

Наиболее часто в практических задачах используются:

а) правило отделения;

б) правило подстановки.

Правило отделения имеет следующий логический смысл: если посылка верна, то верно и следствие из неё.

Пример.

Рассуждения с помощью правила отделения:

«Если студент не выучил теорию, то он не выполнит задание. Студент не выучил теорию. Следовательно, студент не выполнит задание».

«Если студент получил пять, значит, он решил задачу. Студент получил пять. Следовательно студент решил задачу».

Правило подстановки выражает тот факт, что если в тождественно истинной формуле все вхождения какого-либо атома заменить на некоторую формулу, то полученное выражение останется тождественно истинным.

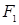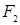Рассмотрим правило подстановки. Пусть и − формулы логики высказываний, − атомарная формула. Если 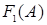− формула, выводимая в исчислении высказываний, содержащая атом , то 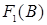− выводимая формула, полученная заменой всех вхождений в формуле 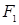на формулу 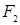. Правило подстановки записывается следующим образом: .

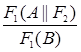Пример.

Используя правило подстановки и коммутативный закон для дизъюнкции, доказать общезначимость следующей формулы: .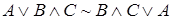

Запишем тождество, соответствующее коммутативному закону длдя дизъюнкции: 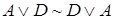. Определим подстановку − атомарную формулу 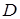заменим на 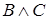: 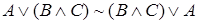. Если опустить скобки в соответствии с приоритетом операций, то можно убедиться в истинности исходной формулы.

Кроме рассмотренных правил вывода в исчислении высказываний часто используются правила дедуктивного вывода, представленные в табл. 11.1.

Таблица 11.1 − Правила дедуктивных выводов логики высказываний

Правило дедуктивного вывода	Тавтология	Название правила
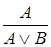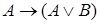		Правило введения дизъюнкции
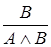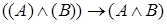,		Правило введения конъюнкции
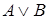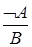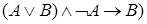,		Правило удаления дизъюнкции (дизъюнктивный силлогизм)
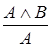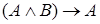		Правило удаления конъюнкции
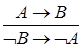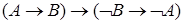		Правило контрапозиции импликации
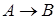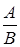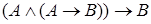,		Правило отделения (Modus Ponens)
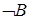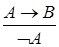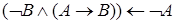,		Отрицательная форма правила отделения (ModusTollens)
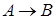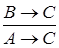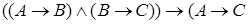,		Гипотетический силлогизм

11.4 Непротиворечивость, независимость

Проблема непротиворечивости возникает при рассмотрении любого исчисления (это одна из кардинальных проблем математической логики).

Определение.

Логическое исчисление непротиворечиво, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой.

Непротиворечивое исчисление − это такое исчисление, что, какова бы ни была формула , никогда формулы и 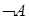не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил.

Если в системе обнаруживаются выводимые формулы вида и 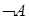то такое исчисление называется непротиворечивым. Такие исчисления никакой ценности не представляют, т.к. они не могут отражать в себе различие между истиной и ложью.

Теорема.

Исчисление высказываний непротиворечиво.

Рассмотрим свойство независимости системы аксиом исчисления высказываний.

Определение.

Если ни одну из аксиом системы исчисления высказываний нельзя вывести из остальных, применяя правила вывода данной системы, то говорят, что система аксиом независима.

Аксиомы исчисления высказываний подбираются таким образом, чтобы они были независимы.

11.5 Различные аксиоматизации исчисления высказываний

Существуют различные аксиоматизации исчисления высказываний, т.е. исчисление высказываний можно описать различными системами аксиом, используя различные наборы символов алфавита, лишь бы с их помощью можно было выразить все остальные логические операции.

Пример.

1. Аксиоматизация исчисления высказывания Гилберта и Аккермана (1938):

а) связки ;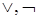

б) аксиомы:

,

,

,

;

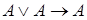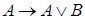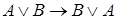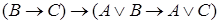в) правило: Modus Ponens (правило отделения).

2. Аксиоматизация исчисления высказывания Россера (1953):

а) связки ;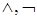

б) аксиомы:

,

,

;

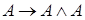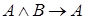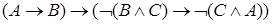в) правило: Modus Ponens (правило отделения).

3. Аксиоматизация исчисления высказывания Клини (1952)

а) связки ;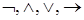

б) аксиомы:

,

,

,

,

,

,

,

,

,

.

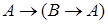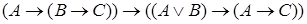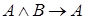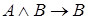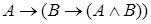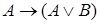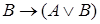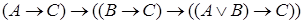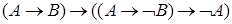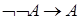в) правило: Modus Ponens (правило отделения).

Приведем в качестве примера следующую формальную систему исчисления высказывания:

1. Язык системы состоит из правильно построенных формул логики высказываний, содержащих операции 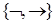. Алфавит языка совпадает с алфавитом логики высказываний и содержит, кроме символов перечисленных логических операций, символы скобок и символы для обозначения высказываний.

2. Аксиомы системы :

а) ;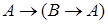

б) ;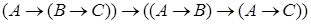

в) .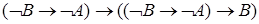

3. Правила вывода:

а) правило отделения (Modus Ponens);

б) правило подстановки.

Достоинством данной формальной системы является лаконичность при сохранении определенной наглядности.

11.6 Некоторые приемы доказательств в исчислении высказываний

Для доказательства истинности утверждений в исчислении высказываний существуют определенные приемы. Один из них использует теорему о дедукции.

Теорема о дедукции.

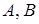Пусть − множество формул, − формулы и 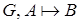. Тогда .

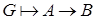Эта теорема обосновывает следующий прием: в математических рассуждениях часто какое-то утверждение доказывают в предположении некоторого другого утверждения , после чего заключают, что верно утверждение «если то ».

Вместо прямого логического вывода формулы из формулы часто оказывается удобным доказать противоречивость формулы 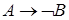тем самым доказав истинность формулы 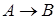. Такой метод (прием) доказательства называется методом от противного и может быть реализован следующими схемами:

1) 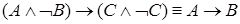− если из предположения, что − верно, а − неверно, следует два противоречащих друг другу высказываний, то это означает, что из следует ;

2) 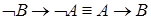− если из предположения, что − неверно, следует, что неверно, то это означает, что из следует .