Цикл. Путь. Длина пути. Связность графа. Мост. Деревья, лес
Путемв графе называется такая последовательность ребер, ведущая от некоторой начальной вершины Р1 в конечную вершину Рn, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза. Например, в графе, изображенном на рис.
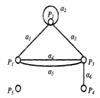
последовательность ребер (а1, а2, а3, а4, а5, а6) образует путь, ведущий от вершины Р1 к вершине Р4.
Циклом называется путь, начальная и конечная вершины которого совпадают. На рис. ребра (a1, a3, a4) образуют цикл.
Цикл графа G называется простым, если он не проходит ни через одну вершину G более одного раза.
Длиной пути или цикла называется число ребер этого пути или цикла.
Граф G называется связным, если для любых двух его вершин существует путь, их соединяющий. В противном случае граф G называется несвязным.
Связный граф без циклов называется деревом.
Граф называется деревом, если
1. в нем есть одна вершина, в которую не входят ребра; она называется корнем дерева;
2. в каждую из остальных вершин входит ровно по одному ребру;
3. все вершины достижимы из корня.
Граф, являющийся объединением нескольких непересекающихся деревьев, называется лесом.
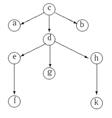
В дереве на рис. вершина  является корнем, вершины
является корнем, вершины 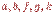 - листья. Путь
- листья. Путь 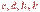 - одна из ветвей дерева
- одна из ветвей дерева 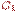 .
.
Плоский граф. Формула Эйлера о числе ребер и числе граней для плоского представления плоского связного графа.
Плоский граф — это граф, нарисованный таким образом, что его ребра не пересекаются. Говорят, что граф допускает плоскую укладку, если его можно нарисовать как плоский. Также плоские графы называют планарными. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого "выходят" деревья
Формула Эйлера
Для всякого плоского представления связного плоского графа без перегородок число вершин (V), число ребер (E) и число граней с учетом бесконечной (R) связаны соотношением V-E+R=2
Пусть граф G— связный, плоский граф без перегородок. Определим значение алгебраической суммы V-E+R для его произвольного плоского представления.
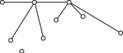
Преобразуем данный граф в дерево, содержащее все его вершины. Для этого удалим некоторые ребра графа G, разрывая поочередно все его простые циклы, причем так, чтобы граф оставался связным и без перегородок.
Заметим, что при таком удалении одного ребра число граней уменьшается на 1, так как при этом либо пропадет один простой цикл, либо два простых цикла преобразуются в один. Следовательно, значение разности E-R при этом остается неизменным.
На рисунке ребра, которые мы удаляем, изображены кривыми. В полученном дереве обозначим число вершин —Vd, число ребер —Ed, число граней — Rd. Справедливо равенство.E-R= Ed- Rd
В дереве одна грань, то естьE-R= Ed- 1. Операция удаления ребер из графа не меняет число его вершин, то есть V=Vd. B дереве 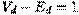 . Отсюда
. Отсюда 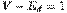 , то есть
, то есть 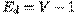 , а потому
, а потому  или
или 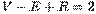 .
.
Итак, доказано, что если в плоском представлении связного графа без перегородок V вершин, E ребер и R граней, то 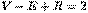 . Полученная формула называется формулой Эйлера.
. Полученная формула называется формулой Эйлера.
