Примеры бинарных отношений. 9 страница

Булевы функции можно рассматривать как логические операции над величинами, принимающими два значения – 0 и 1. Основными в двузначной логике являются три функции:

- отрицание (функция 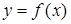, принимающая значения 1, когда 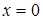, и значение 0, когда );

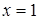- дизъюнкция (функция 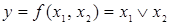, принимающая значение 0 тогда и только тогда, когда оба аргумента имеют значение 0);

- конъюнкция (функция 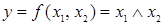, принимающая значение 1 тогда и только тогда, когда оба аргумента имеют значение 1).

Задание булевой функции порядковым номером. Каждой функции присваивается порядковый номер в виде натурального числа, двоичный код которого представляет собой столбец значений функции в таблице истинности. Младшим разрядом считается самая нижняя строка (значение функции на интерпретации 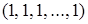, а старшим - самая верхняя (значение функции на интерпретации 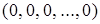). Указанный порядковый номер функции, как двоичный, так и десятичный, полностью определяет булеву функцию.

Часто для упрощения записи булевой функции вместо полного перечисления интерпретаций используют только двоичные значения наборов, для которых функция принимает единичные значения. Такую форму записи называют числовой.

Пример.

Найдем порядковый номер функции 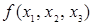, которая задана таблицей истинности (см. табл. 6.1). Для этого переведем двоичное число 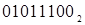в десятичную систему счисления:

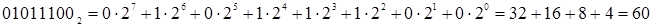Кортеж значений аргументов (интерпретацию) также можно рассматривать как запись целого положительного числа в двоичной системе счисления. Первая интерпретация в таблице истинности называется нулевой, последняя – единичной (номер интерпретации 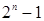, где – количество аргументов функции).

Определение.

Десятичный эквивалент двоичного представления интерпретации называется номером интерпретации (кортежа).

Пример.

Шестой интерпретацией является 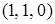, т.е. .

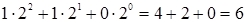Пример.

Пусть функция 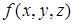принимает единичные значения на интерпретациях 1, 4, 7. Тогда, используя числовую форму записи, функция будет иметь вид: 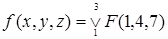, что означает, что функция принимает единичные значения на наборах 1, 4 и 7.

6.5 Реализация булевых функций формулами

Булевы функции могут быть заданы аналитически, т.е. формулами (аналитическими выражениями).

Определение.

Формула – это выражение, содержащее булевы функции и их суперпозиции.

Пример.

Формулы булевой алгебры можно представить следующим образом:

; [ ], .

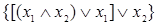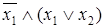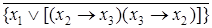Определение.

Суперпозицией называется прием получения новых функций путем подстановки значений одних функций вместо значений аргументов других функций.

Пример.

Рассмотрим формулу, задающую функцию 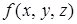следующим образом 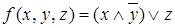. Эта формула содержит функции: 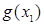- отрицание, 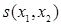- конъюнкцию, 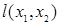- дизъюнкцию. Данную формулу можно представить в виде суперпозиции указанных функций следующим образом: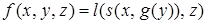

Как и в элементарной алгебре, в алгебре логики можно строить формулы, исходя из элементарных функций.

При образовании (построении) формул используются знаки (символы) трех категорий:

1) символы первой категории обозначают переменные: ;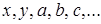

2) символы логических операций 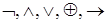и т.д.;

3) пары символов (), [], {}.

Если в формуле отсутствуют скобки, то операции выполняются в следующей последовательности: отрицание, конъюнкция, дизъюнкция, импликация, и эквивалентность: .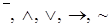

Определение.

Запись формул, при которой знаки функций стоят между аргументами, называют инфиксной (в дальнейшем будем пользоваться такой формой записи).

Формула каждому набору значений аргумента ставит в соответствие значение функции и, следовательно, может служить, наряду с таблицей, способом задания и вычисления функций. По формуле можно восстановить таблицу функций.

Определение.

О формуле, задающей функцию, говорят также, что она реализует или представляет эту функцию.

В отличие от табличного задания представление булевой функции формулой не единственно.

Определение.

Формулы, представляющие одну и ту же функцию, называются эквивалентнымиили равносильными.

Две функции (как и определяющие их формулы) считаются равносильными, если при любых значениях аргументов эти функции (формулы) принимают одинаковые значения. Равносильные функции соединяются знаком равенства.

Пример. Равносильные функци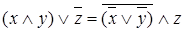и или .

Пример.

Важнейшие примеры равносильных функций: 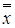равносильно ; 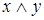равносильно 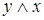; 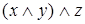равносильно 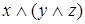; 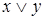равносильно 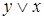; 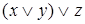равносильно 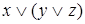; 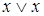равносильно ; 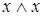равносильно ; 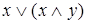равносильно .

Чтобы выяснить, являются ли данные формулы эквивалентными (равносильными), существует, по крайней мере, два метода:

- стандартный метод (построение таблицы функции);

- метод эквивалентных преобразований формул.

6.6 Принцип двойственности

Одним из способов получения тождеств в булевой алгебре является способ, основанный на принципе двойственности.

Определение.

Функция 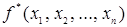называется двойственной к функции 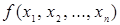, если .

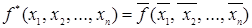Для любой функции двойственная ей функция определяется однозначно.

Отношение двойственности симметрично.

Определение.

Функция, двойственная сама себе, т.е. 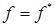, называется самодвойственной.

Самодвойственные функции принимают противоположные значения на любых двух противоположных наборах. Если в таблице истинности функции наборы, как обычно, следуют в порядке их номеров, то противоположные друг другу наборы располагаются симметрично относительно середины их расположение. Это значит, что строка значений самодвойственной функции должна быть антисимметричной относительно своей середины.

Пример.

а) 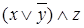двойственна .

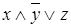б) 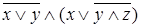двойственна .

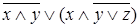Таблица двойственности функции получается из таблицы для функции 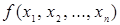инвертированием (т.е. заменой 0 на 1 и 1 на 0) значений функции и заменой порядка следования инвертированных значений функции на противоположный (переворачиванием столбца инвертированных значений функции).

Пример.

Найдем функцию 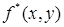, двойственную заданной 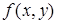, при помощи таблицы истинности. Результат представим в табл. 6.5.

Таблица 6.5 - Таблица истинности 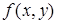и двойственной функции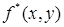

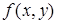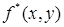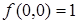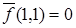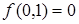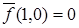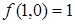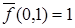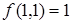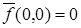Рассмотрим таблицу истинности самодвойственной функции (табл. 6.6).

Таблица 6.6 - Самодвойственная функция, представленная таблицей истинности

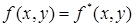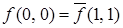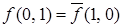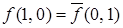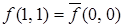Определение.

Принцип двойственности указывает правило получения двойственных формул в булевой алгебре: «Для того чтобы получить двойственную формулу булевой алгебры, необходимо заменить в ней все конъюнкции на дизъюнкции, дизъюнкции на конъюнкции, 0 на 1, 1 на 0 и использовать скобки, где необходимо, чтобы порядок выполнения операций остался прежним».

Пример.

Найти функцию, двойственную функции .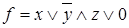

Используя правило получения двойственных функций, получим двойственную функцию .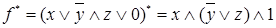

Определение.

Если функции равны, то и двойственные им функции также равны, т.е., если 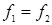, то .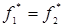

Принцип двойственности позволяет почти в два раза сократить усилия на вывод тождеств при рассмотрении свойств элементарных функций.

6.7 Булевы алгебры. Законы и тождества булевой алгебры

Определение.

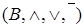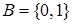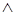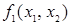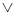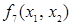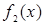Алгебраическая структура , где и операция есть конъюнкция , есть дизъюнкция (таблица 3.4), « » есть отрицание (таблица 3.2), называется двухэлементной булевой алгеброй.

Определение.

Алгеброй логики называется двухэлементная булева алгебра 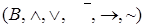, где носитель алгебры 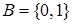, и в которой множество операций дополнено двумя бинарными операциями: импликацией 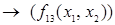и эквивалентностью 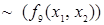(см. таблицу 3.4).

На основе определения основных операций (отрицание, дизъюнкция, конъюнкция) нетрудно убедиться в справедливости следующих законов (свойств) булевой алгебры.

Рассмотрим основные законы (свойства) булевой алгебры.

Закон коммутативности (переместительный закон)

;

.

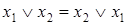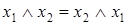Пример.

Доказать коммутативность операции дизъюнкции можно, используя таблицы истинности (табл. 6.7).

Таблица 6.7 - Таблица истинности для доказательства коммутативности операции дизъюнкции

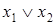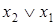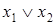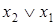Столбцы и в таблицах истинности содержат одинаковые значения, что доказывает коммутативность операции дизъюнкции.

Найдем тождество, двойственное данному тождеству, для чего заменим все функции на двойственные им , .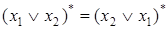

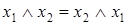Закон ассоциативности (сочетательный закон)

;

.

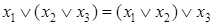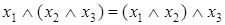Пример.

Доказать ассоциативность операции конъюнкции можно, используя таблицы истинности (табл. 6.8).

Таблица 6.8 - Таблица истинности для доказательства ассоциативности операции конъюнкции

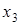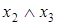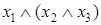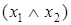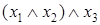Столбцы, соответствующие левой и правой частям второго равенства, содержат одинаковые значения, что доказывает справедливость тождества .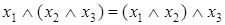

Тождество, выражающее ассоциативность дизъюнкции, двойственно доказанному, так как может быть получено из него путем замены всех функций на двойственные им, и, следовательно, оно тоже верно.

Закон дистрибутивности (распределительный закон)

;

.

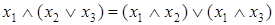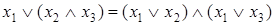Пример.

Доказательство дистрибутивности конъюнкции относительно дизъюнкции можно провести, используя таблицы истинности (табл. 6.9).

Таблица 6.9 - Дистрибутивность конъюнкции относительно дизъюнкции

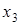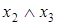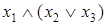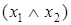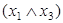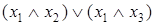Столбцы, соответствующие левой и правой частям первого равенства, содержат одинаковые значения, что и доказывает справедливость равенства 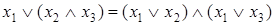. Двойственное тождество выражает дистрибутивность дизъюнкции относительно конъюнкции.

Закон идемпотентности

;

.

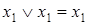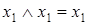Пример.

Для доказательства закона идемпотентности используем таблицу истинности (табл. 6.10).

Таблица 6.10 - Закон идемпотентности

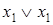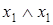В таблице значения всех столбцов одинаковы и совпадают со значением переменной , что и доказывает оба тождества. Данные тождества являются двойственными друг другу.