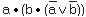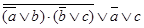Основы математической логики
1. Установите, какие из следующих предложений являются логическими высказываниями, какие – предикатами, а какие не являются ни тем, ни другим (объясните почему):
1)"Солнце есть спутник Земли";
2) 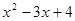
3) 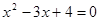
4) "в романе Л.Н. Толстого "Война и мир" 3 432 536 слов";
5) "Санкт-Петербург расположен на Неве";
6) "музыка Баха слишком сложна";
7) "первая космическая скорость равна 7.8 км/сек";
8) "любое простое число р не имеет делителей, отличных от себя и 1";
9) «Натуральное число n не меньше 1»
10) "если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный";
11) «Треугольник АВС подобен треугольнику А1В1С1»;
12) 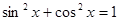 .
.
2. Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3.Для каждого из предикатов в задании 1 найдите какие-либо значения переменных, при которых он обращается в истинное высказывание, и значения переменных, при которых он обращается в ложное высказывание,
4. Сформулируйте отрицания следующих высказываний или предикатов:
а) “Эльбрус — высочайшая горная вершина Европы”;
б) “2≥5”;
в) “10<7”;
г) “все натуральные числа целые”;
д) “через любые три точки на плоскости можно провести окружность”;
е) “теннисист Кафельников не проиграл финальную игру”;
ж) “мишень поражена первым выстрелом”;
з) “это утро ясное и теплое”;
и) “число n делится на 2 или на 3”;
к) “этот треугольник равнобедренный и прямоугольный”;
л) "на контрольной работе каждый ученик писал своей ручкой".
5. Выделите в составных высказываниях простые. Обозначьте каждое из них буквой; запишите с помощью логических операций каждое составное высказывание.
1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
3) Если сумма цифр числа делится на 3, то число делится на 3.
4) Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
5) Если летом мы поедем в Париж и у нас будет достаточно времени, то мы посетим Лувр
6) Если целое число больше 1, то оно простое либо составное
7) Новые палатки и новые рюкзаки будут приобретены в том и только в том случае, если класс пойдет в поход.
6. Даны два простых высказывания:
А = {2 • 2 = 4}, В = {2 • 2 = 5}.
Какие из составных высказываний истинны:
а.) А; б) В ; в) А ∙ В; г) A v B; д) А∙В; е) АVВ; ж) А→В; з) В↔А ?
7. Определите, истинно или ложно высказывания А, если высказывание:
1) А и 2∙2≤5 истинно; 2) А или 32<7 истинно; 3) А или 2∙2≥5 ложно; 3) А→2∙2=4 ложно; 4) А↔32<7 истинно.
8. Определите, какие из высказываний в следующих парах являются отрицаниями друг друга, а какие нет:
а) “5<10”, “5>10”;
б) “10>9”, “10≤ 9”;
в) “мишень поражена первым выстрелом”, “мишень поражена вторым выстрелом”;
г) “машина останавливалась у каждого из двух светофоров”, “машина не останавливалась у каждого из двух светофоров”,
д) “человечеству известны все планеты Солнечной системы”, “в Солнечной системе есть планеты, неизвестные человечеству”;
е) “существуют белые слоны”, “все слоны серые”;
ж) “кит — млекопитающее”, “кит — рыба”;
з) “неверно, что точка А не лежит на прямой а”, “точка А лежит на прямой а”;
и) “прямая а параллельна прямой b”, “прямая a перпендикулярна прямой b”;
к) “этот треугольник равнобедренный и прямоугольный”, “этот треугольник не равнобедренный или он не прямоугольный”.
8. Подставьте в приведённые ниже предикаты вместо логических переменных a, b, c, d такие высказывания, чтобы полученные таким образом составные высказывания имели смысл в повседневной жизни:
а) если (а или (b и с)), то d;
б) если (не а и не b), то (с или d);
в) (а или b) тогда и только тогда, когда (с и не d).
9 Составьте таблицы истинности логических выражений:
1) 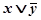 2) 2) 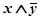 3) 3) 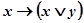 | 4) А˅ (B ˅ C) 5) (А ˅ B) ˅ (A ˅ B) 6) (А ˅ B) ˅ (C Λ B) | 7) 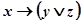 8) 8) 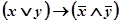 9) 9) 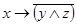 |
10. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными:
|
11.Изобразите на плоскости множества истинности предикатов:
1) 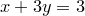 2) 2) 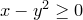 3) 3)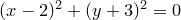 | 4) 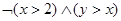 5) 5) 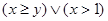 6) 6) 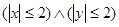 | 7) 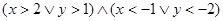 8) 8) 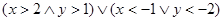 |
12. Упростите формулы, используя законы алгебры логики: а) 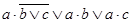 ; б) ((А) Λ С) V B Λ (C); в)
; б) ((А) Λ С) V B Λ (C); в) 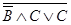 : г) x ® x Ú y; д)
: г) x ® x Ú y; д) 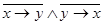 ; е) (x Ú y)∙(x ~ y)
; е) (x Ú y)∙(x ~ y)
13. Определить участника преступления, исходя из двух посылок:
1) "Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал";
2) "Если Иванов не участвовал, то Сидоров не участвовал"
14. Мама, прибежавшая на звон разбившейся вазы, застала всех трех своих сыновей в совершенно невинных позах: Саша, Ваня и Коля делали вид, что происшедшее к ним не относится. Однако футбольный мяч среди осколков явно говорил об обратном.
Кто это сделал? спросила мама.
Коля не бил по мячу, сказал Саша. Это сделал Ваня.
Ваня ответил: Разбил Коля, Саша не играл в футбол дома.
Так я и знала, что вы друг на дружку сваливать будете, рассердилась мама. Ну, а ты что скажешь? спросила она Колю.
Не сердись, мамочка! Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки, сказал Коля.
Оказалось, что один из мальчиков оба раза солгал, а двое в каждом из своих заявлений говорили правду.
Кто разбил вазу?.
15. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?

 б)
б) 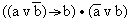
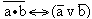 г)
г)