· тактовая частота процессора – чем выше тактовая частота, тем выше производительность и цена микропроцессора. Тактовая частота измеряется в мегагерцах (МГц).
· объем оперативной памяти;
· материнская плата.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
| Монтаж, наладка и эксплуатация САУ |
10. Законы алгебры логики
Основные положения и законы алгебры логики
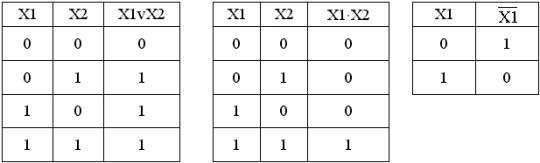
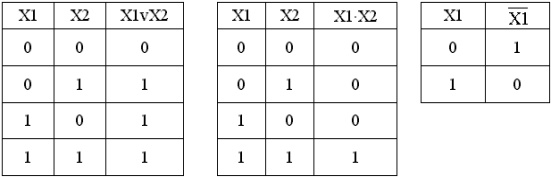
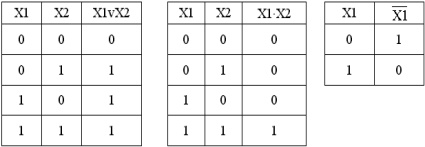
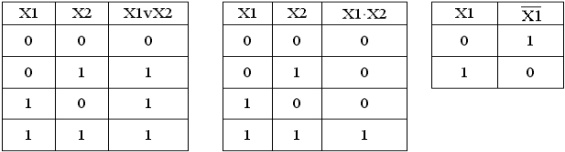
Основным математическим аппаратом, используемым при анализе и синтезе дискретных элементов и устройств является алгебра логики (булева алгебра, алгебра Буля). В алгебре логики широко используется понятие “высказывание”. Высказыванием будем называть простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Любое высказывание можно обозначить символом X и считать, что X=1, если высказывание истинно, а X=0, если высказывание ложно. Логическая (булева) переменная – такая переменная X, которая может принимать только два значения: X={0,1}. Из двух простых высказываний X1 и X2 можно образовать более сложные высказывания, используя операции “И”, “ИЛИ”, “НЕ”. Сложные высказывания также принимают значения “истинно” или “ложно”, т.е. 1 или 0. Смысл логических операций над простыми высказываниями X1 и X2 и значениями сложных высказываний можно представить в виде таблиц истинности: “ИЛИ”, “И”, “НЕ” соответственно.
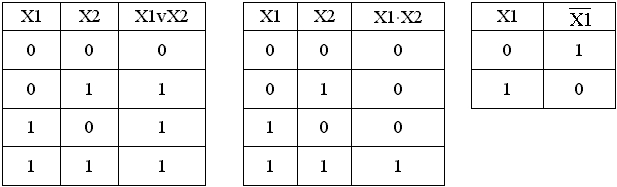
Таким образом, простые высказывания являются переменными, а более сложные высказывания – функциями. Причем как переменные, так и функции могут принимать только значения 0 или 1. Алгебра логики может быть определена как алгебра, содержащая 3 операции “И” (конъюнкция), “ИЛИ” (дизъюнкция), “НЕ”(отрицание) над множеством элементов, каждый из которых принимает два значения 0 или 1. Результаты выполнения операций над множеством элементов также принимают два значения 0 или 1.
Рассмотрим следующий пример. Допустим принимается некоторое решение коллективом из 3-х лиц, которые обозначим a, b, c. Решение считается принятым, если “за” не менее 2-х человек. Процесс принятия решений может быть представлен следующей таблицей истинности.
Таблица истинности

Исходя из таблицы истинности, получим следующие функцию алгебры логики (ФАЛ), которая является сложным высказыванием и является математической моделью принятия решения:

Алгебра логики содержит ряд аксиом и правил. Среди них основными являются следующие:
Для логических величин обычно используются три операции:
Конъюнкция – логическое умножение (И) – and, &, ∧.
Дизъюнкция – логическое сложение (ИЛИ) – or, |, v.
Логическое отрицание (НЕ) – not, .
Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
Законы рефлексивности
a ∨ a = a
a ∧ a = a
Законы коммутативности
a ∨ b = b ∨ a
a ∧ b = b ∧ a
Законы ассоциативности
(a ∧ b) ∧ c = a ∧ (b ∧ c)
(a ∨ b) ∨ c = a ∨ (b ∨ c)
Законы дистрибутивности
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
Закон отрицания отрицания
( a) = a
Законы де Моргана
(a ∧ b) = a ∨ b
(a ∨ b) = a ∧ b
Законы поглощения
a ∨ (a ∧ b) = a
a ∧ (a ∨ b) = a
- Закон повторения
- Переместительный закон
- Ассоциативный закон

- Распределительный закон

- Закон поглощения
- Закон склеивания
- Закон двойного отрицания

- Законы операций с константами

- Закон двойственности (закон де Моргана)

Из закона двойственности вытекают следующие следствия

с помощью которых появляется возможность выражать операцию “И” через операции “ИЛИ”, “НЕ” или операцию “ИЛИ” через операции “И”, “НЕ”.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
| Монтаж, наладка и эксплуатация САУ |
11. Минимизация логических функций методом Квайна
Первый этап (получение сокращённой формы)
Представим, что заданная функция 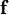 представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:
представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:
1. Операция склеивания;
2. Операция поглощения.
Операция склеивания сводится к нахождению пар членов, соответствующих виду 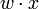 или
или 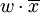 , и преобразованию их в следующие выражения:
, и преобразованию их в следующие выражения: 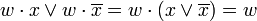 . Результаты склеивания w теперь играют роль дополнительных членов.
. Результаты склеивания w теперь играют роль дополнительных членов.
Потом выполняется операция поглощения. Она основана на равенстве 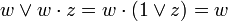 (член
(член 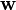 поглощает выражение
поглощает выражение 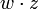 ). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
Обе операции первого этапа могут выполнятся до тех пор, пока это может быть осуществимо.
Применение этих операций продемонстрировано в таблице:
СДНФ выглядит так:
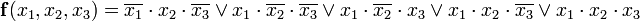 Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)
Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)
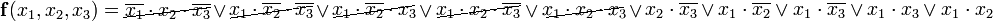
Членами результата склеивания являются 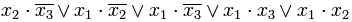
Член 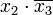 поглощает те члены исходного выражения, которые содержат
поглощает те члены исходного выражения, которые содержат 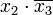 , то есть первый и четвёртый. Эти члены вычёркиваются. Член
, то есть первый и четвёртый. Эти члены вычёркиваются. Член 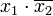 поглощает второй и третий, а член
поглощает второй и третий, а член 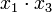 — пятый член исходного выражения.
— пятый член исходного выражения.
Повторение обеих операций приводит к следующему выражению:
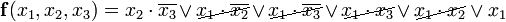
Здесь склеивается пара членов
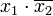
и
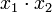
(склеивание пары членов
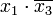
и
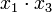
приводит к тому же результату), результат склеивания
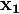
поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой)
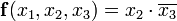
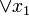
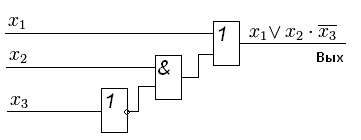
Структурная схема функции
Члены сокращённой формы (в нашем случае это 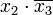 и
и 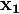 ) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.
) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.
Второй этап (получение минимальной формы)
Как и на первом этапе, в полученном равенстве могут содержаться члены, устранение которых никаким образом не повлияет на конечный результат. Следующий этап минимизации — удаление таких переменных. Таблица, представленная ниже содержит значения истинности функции, по ней будет собрана следующая СДНФ.
СДНФ, собранная по этой таблице выглядит следующим образом:
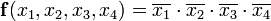
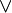
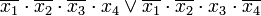
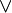
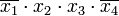
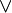
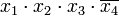
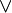
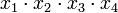
Конечное выражение достигается засчёт повторного использования операций склеивания и поглощения: 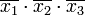
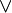
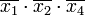
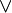
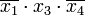
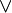
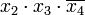
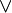
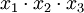
Члены этого выражения являются простыми импликантами выражения. Переход от сокращённой формы к минимальной осуществляется с помощью импликантной матрицы.
Члены СДНФ заданной функции вписываются в столбцы, а в строки — простые импликанты, то есть члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными простыми импликантами. В следующей таблице простая импликанта 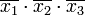 поглощает члены
поглощает члены 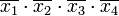 и
и 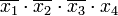 (в первом и во втором столбцах поставлены крестики).
(в первом и во втором столбцах поставлены крестики).
Импликантная матрица
Вторая импликанта поглощает первый и третий члены СДНФ (указано крестиками) и т. д. Импликанты, не подлежащие исключению, образуют ядро. Такие импликанты определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этой импликантой.
В нашем примере ядро составляют импликанты
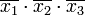
и
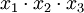
(ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.
Для получения минимальной формы достаточно выбрать из импликантов, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвёртый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать имликанту
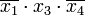
.
Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции:
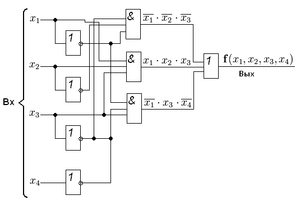
Нажмите на изображение для его увеличения
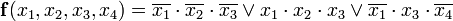 (а)
(а)
Структурная схема, соответствующая этому выражению приведена на рисунке слева. Переход от сокращённой схемы к МДНФ был осуществлён путём исключения лишних членов — импликант 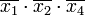 и
и 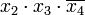 . Покажем допустимость подобного исключения членов из логического выражения.
. Покажем допустимость подобного исключения членов из логического выражения.
Импликанты 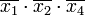 и
и 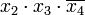 становятся равными лог. 1 соответственно при следующих наборах значений аргументов:
становятся равными лог. 1 соответственно при следующих наборах значений аргументов: 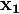 = 0,
= 0, 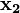 = 0,
= 0, 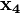 = 0 и
= 0 и 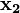 = 1,
= 1, 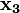 = 1,
= 1, 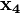 = 0.
= 0.
Роль этих импликант в выражении сокращённой формы функции заключается лишь в том, чтобы на приведённых наборах значений аргументов присваивать функции 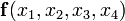 значение 1. Однако при этих наборах функция равна 1 из-за остальных
значение 1. Однако при этих наборах функция равна 1 из-за остальных
импликант выражения. Действительно, подставляя набор значений, указанных выше в формулу (а), получаем:
· при 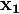 = 0,
= 0, 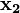 = 0,
= 0, 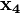 = 0
= 0
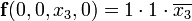
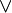
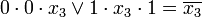
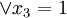 ;
;
· при 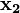 = 1,
= 1, 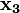 = 1,
= 1, 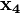 = 0
= 0
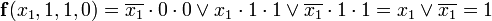 ;
;













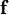 представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:
представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия: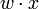 или
или 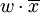 , и преобразованию их в следующие выражения:
, и преобразованию их в следующие выражения: 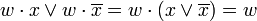 . Результаты склеивания w теперь играют роль дополнительных членов.
. Результаты склеивания w теперь играют роль дополнительных членов.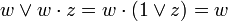 (член
(член 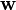 поглощает выражение
поглощает выражение 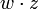 ). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.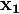
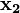
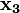
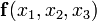
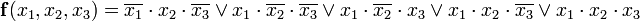 Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)
Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)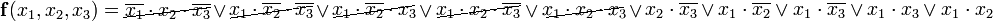
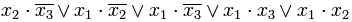
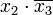 поглощает те члены исходного выражения, которые содержат
поглощает те члены исходного выражения, которые содержат 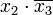 , то есть первый и четвёртый. Эти члены вычёркиваются. Член
, то есть первый и четвёртый. Эти члены вычёркиваются. Член 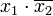 поглощает второй и третий, а член
поглощает второй и третий, а член 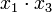 — пятый член исходного выражения.
— пятый член исходного выражения.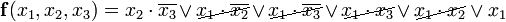
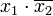 и
и 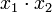 (склеивание пары членов
(склеивание пары членов 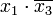 и
и 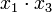 приводит к тому же результату), результат склеивания
приводит к тому же результату), результат склеивания 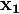 поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой)
поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой) 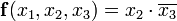
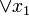

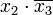 и
и 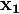 ) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.
) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.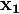
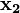
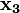
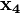
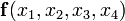
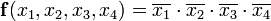
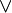
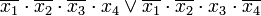
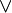
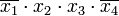
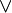
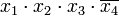
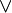
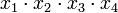
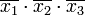
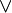
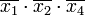
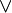
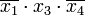
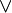
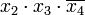
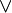
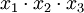
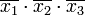 поглощает члены
поглощает члены 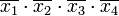 и
и 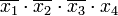 (в первом и во втором столбцах поставлены крестики).
(в первом и во втором столбцах поставлены крестики).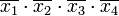
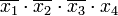
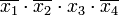
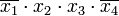
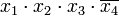
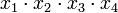
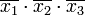
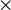
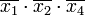
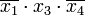
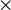
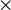
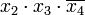
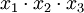
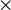
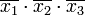 и
и 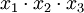 (ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.
(ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.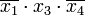 .
.
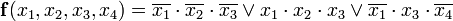 (а)
(а)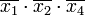 и
и 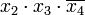 . Покажем допустимость подобного исключения членов из логического выражения.
. Покажем допустимость подобного исключения членов из логического выражения.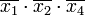 и
и 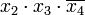 становятся равными лог. 1 соответственно при следующих наборах значений аргументов:
становятся равными лог. 1 соответственно при следующих наборах значений аргументов: 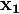 = 0,
= 0, 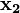 = 0,
= 0, 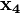 = 0 и
= 0 и 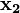 = 1,
= 1, 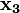 = 1,
= 1, 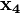 = 0.
= 0.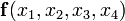 значение 1. Однако при этих наборах функция равна 1 из-за остальных
значение 1. Однако при этих наборах функция равна 1 из-за остальных 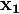 = 0,
= 0, 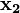 = 0,
= 0, 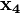 = 0
= 0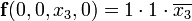
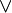
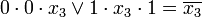
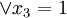 ;
;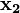 = 1,
= 1, 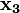 = 1,
= 1, 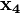 = 0
= 0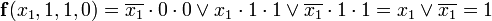 ;
;