Правила выполнения арифметических операций.

ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЦИФРОВЫХ СИСТЕМАХ.

В различные исторические периоды развития человечества для подсчетов и вычислений использовались различные способы представления чисел.

Совокупность приемов и правил наименования и обозначения чисел, с помощью которых можно установить взаимно однозначное соответствие между любым числом и его представлением в виде конечного числа символов называют СИСТЕМОЙ СЧИСЛЕНИЯ.

Существуют различные системы счисления. Примеры:

Счет предметов с помощью палочек:

│ │ │ │ │ │ │ │ │ │ │ │ = 12 = XII

ДВЕНАДЦАТЕРИЧНАЯ система: английская система мер:

1 фут = 12 дюймов

1 шиллинг = 12 пенсов

ШЕСТИДЕСЯТЕРИЧНАЯ система: Вавилон

1 час = 60 минут; 1' = 60"

1° = 60' ; 1' = 60"

ДЕСЯТИЧНАЯ система - возникла в Индии, перенесена в Европу арабами, получила название арабской.

Возьмем для примера десятичное число 12 и посмотрим, каким образом оно получается в десятичной системе счисления:

"Две - на - дцать"

12 = 1 * 10¹ + 2 * 10⁰ = 12

где положение чисел 1 и 2 определяется степенью числа 10.

Аналогично: 342 = 3 * 10² + 4 * 10¹ + 2 * 10⁰ = 300 + 40 + 2

Истинное значение каждой цифры определяется ее местом в числе, т.е. степенью числа 10 - основанием системы счисления.

Система счисления, в которой значение цифры в числе опреде-ляется ее местоположением (позицией), называется ПОЗИЦИОННОЙ.

В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ основанием является число 2. В этом случае для записи чисел используют всего две цифры: 0 и 1. Возьмем, например, число 12 и разложим его по степеням 2.

Получим: 12 = 1 * 2³ + 1 * 2² + 0 * 2¹ + 0 * 2⁰

Число 12 в двоичной системе запишется как: 1100₂ = 12₁₀

42 │ 2 - ├─── 42 │ 21 │ 2 ── - ├─── 0 20 │ 10 │ 2 │ ── - ├─── │ 1 10 │ 5 │ 2 │ │ ── - ├─── │ │ 0 4 │ 2 │ 2 │ │ │ ── - ├─── │ │ │ 1 2 │ 1 │ │ │ │ ── │ │ │ │ │ 0 │ V V V V V V 0 1 0 1 0 1 ┐ ┌──────────────────────────┘ └> 101010 = 42

Перевод числа из десятичной в двоичную производится методом последовательного деления числа на 2 до тех пор, пока частное от деления не станет равным 1. Число в двоичной системе записывается в виде остатков от деления, начиная с последнего частного, справа налево:

Дробная часть представляется суммой отрицательных степеней числа 2. Например, 0.25 = 2^-2.

0.8125 = 0.5+0.25+0.0625 = 1*2^-1 + 1*2^-2 + 0*2^-3 + 1*2^-4 = 0.1101

При переводе дробей в двоичный код в большинстве случаев результат получается приблизительный, поэтому необходимо задавать точность преобразования с нужным количеством знаков после запятой.

При написании программ на языках низкого уровня или в кодах МП и при обработке данных широко используются еще две системы счисления.

ВОСЬМИРИЧНАЯ система в качестве основания использует число 8 и, соответственно, 8 цифр от 0 до 7. Перевод из десятичной системы в восьмиричную осуществляется по тому-же правилу, что и в случае с двоичной системой. Перевести число из двоичной в восьмеричную систему еще проще. Надо число, представленное в двоичном виде, сгруппировать справа налево по три цифры и каждую группу отдельно перевести по правилу перевода из двоичной системы в десятичную. Обратное преобразование - в обратном порядке. Например:

число 453₁₀ = 111.000.101₂ = 705₈

ШЕСТНАДЦАТЕРИЧНАЯ система в качестве основания использует число 16 и, соответственно, цифры от 0 до 9 и первые 6 букв латинского алфавита A, B, C, D, E, F. При переводе числа из двоичной системы в шестнадцатиричную надо число, представленное в двоичном виде, сгруппировать справа налево по четыре цифры и каждую группу отдельно перевести по правилу перевода из двоичной системы в десятичную. Например:

число 453₁₀ = 1.1100.0101₂ = 1C5₁₆ = 1C5h = 0x1C5

ДВОИЧНО-ДЕСЯТИЧНАЯ система применяется в тех случаях, когда результат необходимо представить в удобном для восприятия человеком виде (на цифровом индикаторе, ЦПУ и др.). При этом каждая цифра десятичного числа отдельно переводится в двоичный код, причем результат представляется в четырех разрядах и при необходимости дополняется нужным количеством нулей. Окончательный результат получается при записи полученных двоичных чисел подряд, в том порядке, какой был в десятичном числе. Например:

4 5 3

число 453₁₀ = 0100.0101.0011_2-10

.

ПРАВИЛА ВЫПОЛНЕНИЯ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ.

СЛОЖЕНИЕ чисел, представленных в двоичном коде, выполняется поразрядно, начиная с младшего разряда. В результате сложения двух первых кодов слагаемых X₀, Y₀ получается первый разряд суммы S₀ и код переноса P₀ в следующий разряд. В следующих разрядах код S_i будет определяться с учетом переноса из соседнего младшего разряда:

7 0111

5 0101

+ ── + ─────

12 1100

ОПЕРАЦИЯ ВЫЧИТАНИЯ в ЭВМ выполняется так же как и сложение, но при этом отрицательные числа представляются в дополнительном или обратном коде. Смысл перевода отрицательных чисел из прямого в дополнительный и обратный коды поясним на примере с десятичными числами.

Допустим, требуется сложить числа X1=76 и X2=-58. Заменим код отрицательного слагаемого X2 его дополнением до 100, так чтобы [X2]доп=100+X2=42. Сложив числа X1+[X2]доп получим:

Y=X1+[X2]доп=76+42=118

Отбрасывая 1 старшего разряда получим искомый результат 18. Равенство полученного результата истинному объясняется тем, что при формировании дополнительного кода к X2 мы прибавляли 100, а из результата вычитали 100 отбрасыванием старшего разряда.

Y=X1+[X2]доп-100=X1+[X2+100]-100=76+[-58+100]-100=18

При записи двоичного числа в прямом коде в знаковом разряде ставится его знак (0 - плюс, 1 - минус), а само число записывается в естественной форме:

X=13₁₀ [X]пр=01101₂

X=-13₁₀ [X]пр=11101₂

ДОПОЛНИТЕЛЬНЫЙ КОД отрицательных двоичных чисел получается заменой двоичных кодов во всех разрядах на взаимно обратные (0 на 1, 1 на 0). После этого к младшему разряду числа добавляется 1. В знаковом разряде отрицательного числа записывается 1.

[-14]доп=[-01110]доп=[10001+1]=10010

Кроме дополнительного кода для представления отрицательных чисел используется ОБРАТНЫЙ КОД. В этом случае в знаковом разряде записывается 1, а в остальных разрядах цифры заменяются на взаимно обратные

[-14]обр=[-01110]обр=10001

При выполнении арифметических операций с отрицательными числами производится поразрядное сложение слагаемых, начиная с младшего и кончая знаковым разрядом. Если используется дополнительный код, то возможная единица переноса из знакового разряда отбрасывается, при использовании обратного кода единица переноса знакового разряда суммируется с младшим разрядом полученной суммы. Результат вычисления получается в том коде, в каком были представлены слагаемые. Положительные числа в прямом, обратном и дополнительном кодах имеют одну и ту же форму записи. Например:

12 X1пр=0.1100 X1обр=0.1100 X1доп=0.1100

5 X2пр=0.0101 X2обр=1.1010 X2доп=1.1011

- ─── - ─────────── + ──────────── + ────────────

7 Sпр= 0.0111 10.0110 10.0111

└──>──┘ <──┘

Sобр= 0.0111 Sдоп= 0.0111

Y=5-12=-7 X1обр=0.0101 X1доп=0.0101

X2обр=1.0011 X2доп=1.0100

+ ──────────── + ────────────

Sобр= 1.1000 Sдоп= 1.1001

Sпр= -0.0111 Sпр= -0.0111

УМНОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ, представленных в форме с фиксированной точкой, включает в себя определение знака и абсолютного значения произведения. Знаковый разряд произведения может быть получен суммированием знаковых разрядов сомножителей без формирования переноса (так называемое суммирование по модулю 2). Действительно, при совпадении цифр знаковых разрядов сомножителей (0 и 0, либо 1 и 1) их сумма по модулю 2 равна 0, т.е. соответствует знаковому разряду произведения двух сомножителей, имеющих одинаковые знаки; при несовпадении цифр знаковых разрядов эта сумма будет равна 1, что также соответ-ствует знаковому разряду произведения двух сомножителей с разными знаками. Абсолютное значение произведения получается путем перемножения чисел без учета их знаков (так называемого кодового умножения).

Пусть производится умножение чисел 13₁₀ =1101₂ и 11₁₀ =1011₂

13 1101

X X

11 1011

──── ─────

13 1101

+ + 1101

13 0000

──── 1101

143 ────────

Как видно из примера, в процессе выполнения операции умножения формируются частичные произведения (произведения множимого на цифры разрядов множителя), которые суммируются с соответствующими сдвигами друг относительно друга. В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер: формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме прибавляется с соответствующем сдвигом очередное частичное произведение и т.д., пока не окажутся просуммированными все частичные произведения. Этот процесс суммирования можно начинать с младшего либо старшего частичного произведения.

При умножении целых чисел для фиксации произведения в разрядной сетке должно предусматриваться число разрядов, равное сумме числа разрядов множимого и множителя.

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ. Будем рассматривать операцию алгебраического деления чисел, представленных в форме с фиксированной точкой. при этом выполнение операции содержит действия, связанные с определения модуля частного. Знак частного может быть найден тем же приемом, что и знак произведения в рассмотренной выше операции умножения с отделением знаковых разрядов.

На рисунке 1 показана схема алгоритма нахождения частного положительных чисел a и b.

┌─────────────┐

│ S T A R T │

└──────┬──────┘

│

┌1─────────┴──────────┐

│ c = a - b │

└──────────┬──────────┘

│<─────────────────────────────────────┐

2──────/ \──────\ Нет │

< c>=0 >────────────────┐ │

\────── ──────/ │ │

\ / Да │ │

┌3─────────┴──────────┐ ┌4─────────┴──────────┐ │

│Запись 1 в очередной │ │Запись 0 в очередной │ │

│из старших разрядов │ │из старших разрядов │ │

│ частного │ │ частного │ │

└──────────┬──────────┘ └──────────┬──────────┘ │

│ │ │

┌5─────────┴──────────┐ ┌6─────────┴──────────┐ │

│ сдвиг влево c │ │ сдвиг влево c │ │

└──────────┬──────────┘ └──────────┬──────────┘ │

│ │ │

┌7─────────┴──────────┐ ┌8─────────┴──────────┐ │

│ c = c - b │ │ c = c + b │ │

└──────────┬──────────┘ └──────────┬──────────┘ │

│<────────────────────────┘ │

9────────/ \──────── │

/ Сформированы все \ Нет │

< разряды частного ? >───────────────────────────┘

\───────── ────────/

\ / Да

┌─────────┴──────────┐

│ S T O P │

└────────────────────┘ Рисунок 1.

.

Покажем выполнение операции на примере. Пусть после отделения знаковых разрядов модули делимого и делителя представляются соответственно числами a=0.10010 и b=0.10110.

Встречающуюся в алгоритме операцию вычитания числа заменим прибавлением числа -b, представленного в дополнительном коде: (-b)доп=1.01010.

a 0.10010 0. 1 0 1 1 0

(-b)доп 1.01010 ────────────

+ ─────── 0. 1 1 0 1 0 Частное

c 1.11100 c < 0 ───┘ │ │ │ │ │

│ │ │ │ │

Сдвиг влево 1.11000 │ │ │ │ │

b 0.10110 │ │ │ │ │

+ ─────── │ │ │ │ │

c 0.01110 c > 0 ──────┘ │ │ │ │

│ │ │ │

Сдвиг влево 0.11100 │ │ │ │

(-b)доп 1.01010 │ │ │ │

+ ─────── │ │ │ │

c 0.00110 c > 0 ────────┘ │ │ │

│ │ │

Сдвиг влево 0.01100 │ │ │

(-b)доп 1.01010 │ │ │

+ ─────── │ │ │

c 1.10110 c < 0 ──────────┘ │ │

│ │

Сдвиг влево 1.01100 │ │

b 0.10110 │ │

+ ─────── │ │

c 0.00010 c > 0 ────────────┘ │

│

Сдвиг влево 0.00100 │

(-b)доп 1.01010 │

+ ─────── │

c 1.01110 c < 0 ──────────────┘

Проверка: a=0,10010₂ = 0,5625₁₀

b=0,10110₂ = 0,6875₁₀

a/b=0,11010₂ = 0,8125₁₀

.

ОСНОВЫ АЛГЕБРЫ ЛОГИКИ.

Все устройства МП состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: Истинности и ложности выска­зывания. В соответствии с такой двоичной природой высказываний их условились называть ЛОГИЧЕСКИМИ ДВОИЧНЫМИ ПЕРЕМЕННЫМИ и обозначать 1 в случае истинности и 0 в случае ложности. Примерами логических переменных являются высказывания:

А="Земля плоская", В="Парта черная". На основании этих высказы­ваний можно записать А=0; В=1, т.к. высказывание А ложно, а высказывание В истинно.

Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями.

Формализация и преобразование связей между логическими переменными осуществляется в соответствии с правилами АЛГЕБРЫ ЛОГИКИ называемой АЛГЕБРОЙ БУЛЯ.

Две логические переменные А и В принимающие значения 0 или 1, могут образовывать логические функции. Для описания логической функции используют, так называемую, таблицу истинности, в левых колонках которой отображают все возможные значения логических переменных, а справа соответствующие значения функции. Таким образом, каждая строка таблицы соответствует определенному состоянию функции или устройства, ее реализующего.

Наибольший практический интерес представляют функции отрицания, логического умножения и логического сложения..

1.Логическое отрицание НЕ переменной А есть логическая функция Х, которая истинна, когда А ложно, и наоборот. Инвертор.

_ Х = А	Графически функция НЕ обозначается в виде круга возле вывода (МЭК-117-15)(ГОСТ 2.743-91):
A	X	_ А ┌───┐ Х = А ────┤ 1 о───── или └───┘	_ А ┌───┐ Х = А реже ────о 1 ├───── └───┘
		По американской спецификации milspec:

A├────────┐ ┌───────┐ o +Eп

│ └───────┘ └─────── X│ ┌┴┐

└────────────────────────────────> t │ │ │ R

X│ ┌───────┐ ┌─────── V └┬┘

├────────┘ └───────┘ ┌──────/────┴───>

└────────────────────────────────> t ─┴─

2.Логическое умножение И двух переменных А и В есть логическая функция Х, которая истинна только тогда, когда одновременно истинны обе входные переменные. Кроме того функцию И называют КОНЪЮНКЦИЕЙ.

X=A*B или X=A/\B	Графически функция И обозначается в виде значка & внутри элемента
A	B	X		A ┌────┐ ────┤ & │ Х = А /\ B = A * B B │ ├─────────────────── ────┤ │ └────┘
				По американской спецификации milspec: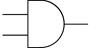

A│ ┌───┐ ┌───────┐ +Eп A B X

├──┘ └─────────┘ └─────── o────/────/───┬───>

└────────────────────────────────> t ┌┴┐

B│ ┌───┐ ┌───────┐ │ │R

├────────┘ └──────┘ └──── └┬┘

└────────────────────────────────> t ─┴─

X│ ┌────┐

├───────────────────┘ └───────

└────────────────────────────────> t

3.Логическая сумма ИЛИ двух переменных А и В есть логическая функция Х, которая истинна, когда истинна хотя бы одна из входных переменных. Кроме того функцию ИЛИ называют ДИЗЪЮНКЦИЕЙ.

X=A+B или X=A\/B	Графически функция ИЛИ обозначается в виде значка 1 внутри элемента
A	B	X		A ┌────┐ ────┤ 1 │ Х = А \/ B = A + B B │ ├─────────────────── ────┤ │ └────┘
				По американской спецификации milspec: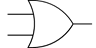

A│ ┌───┐ ┌───────┐ +Eп A X

├──┘ └─────────┘ └─────── o─────┬───/───┬───>

└────────────────────────────────> t │ │

B│ ┌───┐ ┌───────┐ │ B │

├────────┘ └──────┘ └──── └───/───┤

└────────────────────────────────> t ┌┴┐

X│ ┌───┐ ┌───┐ ┌──────────┐ │ │R

├──┘ └─┘ └───┘ └──── └┬┘

└────────────────────────────────> t ─┴─

Три рассмотренных функции позволяют реализовать любую логическую комбинацию. Более того, сочетание одной из функций И либо ИЛИ с функцией НЕ также позволяет реализовать любую сложную функцию. Например, реализуем функцию ИЛИ с помощью элементов И и НЕ.

_

A ┌───┐ A ┌───┐ _ _ ─────

────┤ o─────┤ & │ A * B ┌───┐ A * B = A + B

└───┘ _ │ ├───────┤ o──────────────

B ┌───┐ B │ │ └───┘

────┤ o─────┤ │

└───┘ └───┘

Рассмотрим еще три функции получившие широкое применение в цифровой технике:
4. И-НЕ "Штрих Шеффера"

A	B	X		A ┌────┐ _____ ────┤ & │ Х = A * B B │ о────────── ────┤ │ └────┘
				По американской спецификации milspec:

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X├───────────────────┐ ┌───────

│ └────┘

└────────────────────────────────> t

5. ИЛИ-НЕ "Стрелка Пирса"

A	B	X		A ┌────┐ ______ _____ ────┤ 1 │ Х = А \/ B = A + B B │ о─────────────────── ────┤ │ └────┘
				По американской спецификации milspec:

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X├──┐ ┌─┐ ┌───┐ ┌────

│ └───┘ └───┘ └──────────┘

└────────────────────────────────> t

Две рассмотренные функции интересны тем, что являются достаточными для построения любой сложной функции, т.к. содержат в своем составе функцию И либо ИЛИ и инвертор.

┌───┐ _____ _ ┌───┐ _____ _

A ┌─┤ & │ A * A = A 1 o──┤ & │ A * 1 = A

────┤ │ o────────── │ o──────────

└─┤ │ A ─────┤ │

└───┘ └───┘

6. "ИСКЛЮЧАЮЩЕЕ ИЛИ" или СУММИРОВАНИЕ ПО МОДУЛЮ 2

A	B	X		A ┌────┐ _ _ ────┤ =1 │ Х = A # B = AB + AB = B │ о────────────────────── ────┤ │ ──────── └────┘ = AB + A B
				По американской спецификации milspec: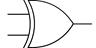

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X│ ┌───┐ ┌───┐ ┌──┐ ┌──┐

├──┘ └─┘ └───┘ └────┘ └────

└────────────────────────────────> t

_

A ┌───┐ A 1 o ┌───┐ A

─────┤=1 ├──── Повторитель A └──┤=1 ├──── Инвертор

┌──┤ │ ───────┤ │

─┴─ └───┘ └───┘

.

Рассмотрим наиболее распространенные правила алгебры логики на примерах с минимальным количеством переменных:

1: X = A * 0 = 0 \

│

2: X = A * 1 = A │ законы

>

3: X = A * A = A │ конъюнкции

_ │

4: X = A * A = 0 /

5: X = A + 0 = A \

│

6: X = A + 1 = 1 │ законы

>

7: X = A + A = A │ дизъюнкции

_ │

8: X = A + A = 1 /

=

9: X = A = A двойная инверсия

10: X = A * B = B * A \ переместительный

>

11: X = A + B = B + A / закон

12: X = (A * B) * C = A * (B * C) \ сочетательный

>

13: X = (A + B) + C = A + (B + C) / закон

14: X = A * (B + C) = AB + AC \ закон дистрибутивности

>

15: X = A + BC = (A + B) * (A + C) / или распределительный

16: X = A + AB = A { A + BA = A (1 + B) } \

│

17: X = A (A + B) = A > законы

_ _ │ погло-

18: X = A + AB = A + B { (1 + A) (A + B) = A + B } / щения

_

19: X = AB + AB = B \ законы

_ > склеивания

20: X = (A + B) (A + B) = B /

__ _ _

21: X = AB = A + B \ правила Де Моргана

_____ _ _ > или

22: X = A + B = A * B / законы инверсии

.

Пример: Задана в виде таблицы истинности логическая функция Y трех переменных A,B,C.

┌───┬───┬───┬───┐ Функция принимает единичное значение при

│ А │ B │ C │ Y │

├───┼───┼───┼───┤ следующих произведениях переменных:

│ 0 │ 0 │ 0 │ 0 │ _ _

├───┼───┼───┼───┤ ABC, ABC, ABC

│ 0 │ 0 │ 1 │ 0 │

├───┼───┼───┼───┤ Каждое из произведений переменных для ║

│ 0 │ 1 │ 0 │ 0 │ ║

├───┼───┼───┼───┤ которых значение функции истинно, носит ║

│ 0 │ 1 │ 1 │ 1 │ ║

├───┼───┼───┼───┤ название МИНТЕРМА. ║

│ 1 │ 0 │ 0 │ 0 │

├───┼───┼───┼───┤ В соответствии с этим, функция может

│ 1 │ 0 │ 1 │ 0 │

├───┼───┼───┼───┤ быть записана в виде уравнения:

│ 1 │ 1 │ 0 │ 1 │ _ _

├───┼───┼───┼───┤ Y = ABC + ABC + ABC

│ 1 │ 1 │ 1 │ 1 │

└───┴───┴───┴───┘

Если при такой записи каждое слагаемое содержит произведения всех переменных или их отрицаний, то такую форму представления функции называют СОВЕРШЕННОЙ ДИЗЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ или ПЕРВОЙ СТАНДАРТНОЙ ФОРМОЙ. Точно так же можно выделять ложные (нулевые) значения функции. Если функция дана в виде произведения (конъюнкции) сумм переменных или их отрицаний, то такую форму представления функции называют СОВЕРШЕННОЙ КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ или ВТОРОЙ СТАНДАРТНОЙ ФОРМОЙ.

A ┌──┐ ┌─────┐ ┌─────┐ Для схемной реализации

───────┬─────┬─┤ о──┤ & │ │ 1 │

B │ │ └──┘ │ │ │ │ полученной функции

─────┬─┼───┬─┼───────┤ ├───┤ │

C │ │ │ │ │ │ │ │ потребуется:

───┬─┼─┼─┬─┼─┼───────┤ │ │ │

│ │ │ │ │ │ ├─────┤ │ │ 3 схемы, выполняющие

│ │ │ │ │ └───────┤ & │ │ │

│ │ │ │ │ │ │ │ │ Y функцию 3И,

│ │ │ │ └─────────┤ ├───┤ ├───

│ │ │ │ ┌──┐ │ │ │ │ 1 схема 3ИЛИ и

│ │ │ └─────┤ о──┤ │ │ │

│ │ │ └──┘ ├─────┤ │ │ 2 схемы НЕ.

│ │ └─────────────┤ & │ │ │

│ └───────────────┤ ├───┤ │

└─────────────────┤ │ │ │

└─────┘ └─────┘

Пользуясь правилами алгебры логики упростим полученную функцию.

_ _ _ _ _ _

Y = ABC + ABC + ABC = ABC + AB (C + C) = ABC + AB = B (AC + A) =

_

= (правило 15) = B (A + A) (C + A) = B (C + A) = BC + AB

Полученная функция и ее схемная реализация значительно проще исходных.

A ┌───┐ ┌───┐ A ┌───┐ ┌───┐

─────┤ & ├───┤ 1 │ ─────┤ & o───┤ & │

B ┌─┤ │ │ │ Y B ┌─┤ │ │ │ Y

───┤ ├───┤ │ ├──── ───┤ ├───┤ │ o────

C └─┤ & ├───┤ │ C └─┤ & o───┤ │

─────┤ │ │ │ ─────┤ │ │ │

└───┘ └───┘ └───┘ └───┘

────────

Y = Y = AB + BC = AB * BC - для построения схемы на одинаковых элементах

Можно было представить ту же самую функцию в СОВЕРШЕННОЙ

КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМЕ в виде произведения сумм:

_ _ _ _ _

Y = (A + B + C) (A + B + C) (A + B + C) (A + B + C) (A + B + C)

Такая запись слишком сложна для минимизации и реализации.

Разработан метод минимизации логических функций, как бы автоматизирующий процедуру поиска "склеивающихся слагаемых - метод КАРТ КАРНО.

Карта Карно - это таблица имеющая ячейки для всех возможных минтермов функции. Можно построить карты Карно для функций, минтермы которых содержат два, три и более переменных (обычно не более 5...6). Составим карту Карно для функции 2-х переменных: Вдоль верхней грани проставлены возможные значения

_

A A переменной А, вдоль левой боковой грани -

┌────┬────┐

│ │ _ │ возможные значения переменной В. В каждой

B │ AB │ AB │

├────┼────┤ клетке изображают один из возможных мин-

_ │ _ │ _ _│

B │ AB │ A*B│ термов: AB, AB, AB, AB. Если какой-то из

└────┴────┘

этих минтермов в совершенной дизъюнктивной

нормальной форме записи функции присутствует, то в соот-

ветствующей клетке карты Карно ставится "1",если нет - то "0".

Составим карты Карно для функций 3-х и 4-х переменных:

-- - - -- - -

AB AB AB AB AB AB AB AB

┌────┬────┬────┬────┐ ┌────┬────┬────┬────┐

- │ ---│ - -│ -│ --│ -- │----│- --│ --│ ---│

C │ ABC│ ABC│ ABC│ ABC│ CD │ABCD│ABCD│ABCD│ABCD│

├────┼────┼────┼────┤ ├────┼────┼────┼────┤

│ -- │ - │ │ - │ - │--- │- - │ - │ -- │

C │ ABC│ ABC│ ABC│ ABC│ CD │ABCD│ABCD│ABCD│ABCD│

└────┴────┴────┴────┘ ├────┼────┼────┼────┤

│-- │- │ │ - │

Склеивание осуществляется между CD │ABCD│ABCD│ABCD│ABCD│

├────┼────┼────┼────┤

теми минтермами, которые запи- - │-- -│- -│ -│ - -│

CD │ABCD│ABCD│ABCD│ABCD│

саны в виде "1" в соседних клет- └────┴────┴────┴────┘

ках карты (по вертикали или горизонтали). Соседними считаются

клетки крайнего левого и правого, верхнего и нижнего рядов

(можно представить карту как развертку цилиндра). Два минтер-

ма, находящиеся в соседних клетках можно представить в виде

одного логического произведения переменных, число которых на

одну единицу меньше, чем в каждом из соседних минтермов, при-

чем в произведении остаются общие для обоих минтермов сомножи-

тели. Если соседними окажутся сразу 4 минтерма с "1" то такую

группу можно заменить произведением переменных, число которых

меньше, чем в каждом минтерме, уже на два. Учитывая, что

А + А +...+ А = А, одну единицу, изображающую минтерм, можно

объединять пары несколько раз.

Используя метод карт Карно минимизируем рассмотренную в

примере функцию. Единица, изображающая минтерм АВС входит сра-

-- - -

AB AB AB AB зу в два объединения, обозначенные

- ┌────┬────┬────┬────┐

C │ 0 │ 0 │ 1 │ 0 │ a и b. Объединение a отражает

├────┼────┼─a│─┼────┤ _

C │ 0 │ 1 ─ 1 │ 0 │ "склеивание" минтермов АВС и АВС

└────┴────b────┴────┘ _ _

АВС + АВС = АВ (С + С) = АВ

_

объединение b отражает склеивание минтермов АВС и АВС

_ _

ABC + ABC = BC (A + A) = BC

В результате проведенных операций "склеивания" из трех минтермов, входящих в функцию и являющихся конъюнкцией трех переменных, остались лишь слагаемые АВ и ВС.

Отсюда: Y = AB + BC.