Представление нечетких множеств

Существуют различные методы описания функции m : U ® [0, 1]. Если U – конечное множество, то функция будет конечным множеством пар:

m = {(x₁, m(x₁)), …, (x_n, m(x_n))}.

и может быть записана как

m = m(x₁)/x₁ + … + m(x_n)/x_n

или в виде таблицы:

x1	x2	…	xn
m(x1)	m(x2)	…	m(xn)

В случае универсума R действительных чисел m(x) задаётся аналитически и изображается в виде графика. Например, 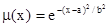будет гауссианой, с m(a) = 1. Лингвистическое выражение «большое число» обозначает понятие, зависящее от параметров, и может быть интерпретировано с помощью функции:

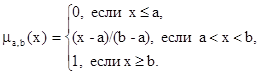
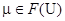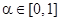Определение. Пусть и . Множество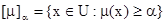

называется a-срезом нечеткого множества m.

Теорема 1. Пусть 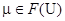, , 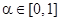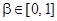. Тогда

1)

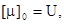
2) если a < b, то ,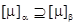

3) .

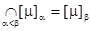Теорема 2 (о представлении). Пусть 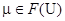. Тогда

.

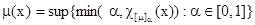Нечеткие множества 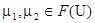называются равными, если 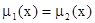для всех 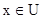; m₁ называется нечетким подмножеством m₂, если 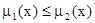для всех 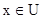, в этом случае применяется запись: .

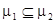Операции над нечеткими множествами

Пусть 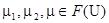. Операции определяются следующим образом:

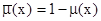(дополнение);

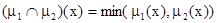(пересечение);

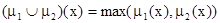(объединение);

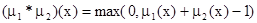(ограниченное произведение);

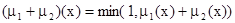(ограниченная сумма);

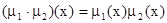(алгебраическое произведение);

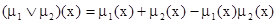(алгебраическая сумма);

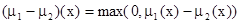(разность);

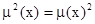(концентрирование).

Поскольку каждое нечеткое множество m можно представить как семейство a-срезов, то операции можно выразить через обычные операции над множествами. В частности:

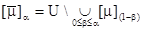(дополнение);

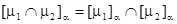(пересечение);

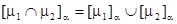(объединение);

Принцип обобщения

Произвольная функция 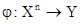между множествами может быть расширена до функции 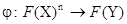следующим образом:

.

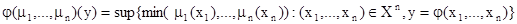Этот метод расширения называется принципом обобщения. Предполагается, что супремум пустого множества равен 0. С помощью принципа обобщения можно расширить операцию сложения 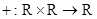, полагая для любых :

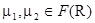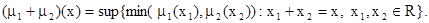
Нечеткое множество 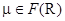называется выпуклым, если все его a-срезы выпуклы. Легко видеть, что сумма 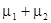нечётких выпуклых множеств m₁ и m₂ из R будет выпуклой.

Логические операции

Рассмотрим расширения определённых на множестве {0, 1} логических операций &, Ú, Ø, ® на интервал [0, 1].

Конъюнкция и дизъюнкция

Операция логического умножения обобщается следующим образом:

Функция 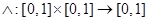называется треугольной нормой, если для всех a, b, c Î [0, 1] справедливы соотношения:

1) a Ù 1 = a (1 – единица);

2) если a £ b, то a Ù c £ b Ù c (монотонность);

3) a Ù b = b Ù a (коммутативность);

4) (a Ù b) Ù с = a Ù (b Ù c) (ассоциативность).

Заметим, что, в силу неравенств 0 £ 0Ùx £ 0Ù1 = 0, имеет место: 0 Ù x = 0.

Наиболее часто используются следующие треугольные нормы:

1) a Ç b = min (a, b) (Заде);

2) a * b = max(0, a + b – 1) (Лукасевич);

3) a × b = ab (произведение чисел).

Аналогично обобщается логическая сумма.

Функция 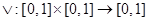называется треугольной конормой, если для всех a, b, c Î [0, 1] справедливы соотношения:

1) 0 Ú a = a (0 – нуль);

2) если a £ b, то a Ú c £ b Ú c (монотонность);

3) a Ú b = b Ú a (коммутативность);

4) (a Ú b) Ú с = a Ú (b Ú c) (ассоциативность).

Примеры треугольных конорм:

1) a È b = max(a, b) (Заде);

2) a Ú b = min(a + b, 1) (Лукасевич);

3) a Ú b = a + b – ab (алгебраическая сумма).

Отрицание

Наиболее общее определение функции отрицания g: [0,1] ® [0,1] предполагает, что выполнены, по крайней мере, два условия:

1) g(0) = 1; g(1) = 0;

2) если a £ b, то g(a) ³ g(b).

Примеры отрицаний:

1) 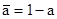(Заде);

2) 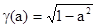(квадратичное отрицание);

3) 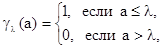(пороговое отрицание);

4) 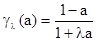, -1 < l < ¥ (Сугено).

Две операции Ù и Ú называются g-двойственными, есл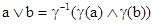и

и .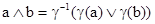

Например, операци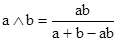и:

и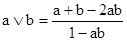

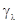-двойственны (относительно отрицания Сугено).

Импликация

Пусть Ù – треугольная норма. Импликацией 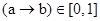, связанной с Ù, называется такое число, что для всех x Î [0, 1] справедлива следующая эквивалентность:

x £ (a ® b), если и только если x Ù a £ b.

В силу монотонности треугольной нормы значение импликации будет равно:

a ® b = sup {x Î [0, 1] : x Ù a £ b }.

Примеры импликаций

1) Cвязанной с треугольной нормой Лукасевича будет импликация:

a ® b = min {1 – a + b, 1}.

2) C треугольной нормой заде связана импликация Гёделя:

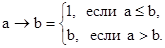
3) C произведением a×b чисел связана импликация Гогена:

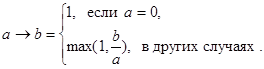
Оператор импликации не всегда связан с треугольной нормой. В частности, импликация Клини-Дайнса определяется по формуле:Øa Ú b, через операцию a Ú b = max(a,b):

a ® b = max(1-a, b).

Аналогичным образом, с помощью формулы Øa Ú b определяется импликация Райхенбаха, где a Ú b = a + b – ab сложение вероятностей:

a ® b = 1 – a + ab.

Импликация Заде аналогична последней:

a ® b = max(1 – a, min(a, b)).

Заметим, что во всех этих случаях отрицание можно определить как Øa = a ® 0.

Нечеткие отношения

Напомним, что отношением между множествами U₁, U₂, …, U_n называется произвольное подмножество R Í U₁ ´ U₂ ´…´ U_n . Поскольку отношение может быть задано с помощью предиката (характеристической функции этого подмножества), то естественным является следующее определение.

Пусть U₁, U₂, …, U_n – универсумы. Нечетким отношением между U₁, U₂, …, U_n называется произвольная функция 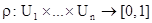. Аналогично теоретико-множественным операциям определяются операции пересечения и объединения. Ограничимся рассмотрением нечетких бинарных отношений r, s Î F(X ´ Y). Положим:

(r È s)(x, y) = max (r(x, y), s(x, y)), (r Ç s)(x, y) = min (r(x, y), s(x, y)).

Эти операции обладают всеми свойствами операций max и min, они коммутативны, ассоциативны, дистрибутивны.

Множество F(X ´ Y) отношений между X и Y упорядочено относительно отношения включения нечетких множеств на X ´ Y. Таким образом, r Í s тогда и только тогда, когда r(x, y) £ s(x, y) для всех x Î X и y Î Y.

Пусть r Î F(X ´ Y) и s Î F(Y ´ Z). Определим композицию r°s Î F(Y ´ Z) как 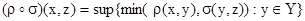. Имеют место соотношения:

1) (r°s)°t = r°(s°t),

2) ,

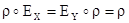где 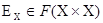принимает значения 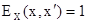при 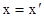, в других случаях ,.

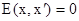Обратное нечёткое отношение определяется как 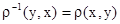, для всех .

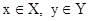Нечёткое отношение r Î F(X ´ Y) называется рефлексивным, если 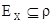. Нечётким отношением эквивалентности называется 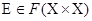, удовлетворяющее условиям:

1) 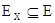(рефлексивность);

2) 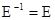(симметричность);

3) 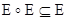(транзитивность).

Если условие 2 заменить на условие антисимметричночти 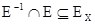, то получим нечёткое отношение порядка.

Заметим, что композицию можно определить с помощью произвольной треугольной нормы, полагая:

.

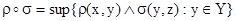Так мы получим другие определения отношений эквивалентности и порядка.

5.4. Пропозициональная нечёткая логика

Формулы пропозициональной нечёткой логики составляются из элементов множества переменных 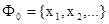и констант 0 (ложь) и 1 (истина) с помощью логических связок Ù, Ú, Ø следующим образом:

1) 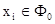формулы для всех i = 1, 2, …;

2) 0 и 1 – формулы;

3) если g и f – формулы, то (f Ù g) и (f Ú g) – формулы;

4) если f – формула, то Øf – формула.

Множество всех формул обозначается через F.

Аксиомы нечёткой пропозициональной логики:

(F1) Ø0 = 1,

(F2) A Ù 1 = A, A Ú 1 = 1, A Ù 0 = 0, A Ú 0 = A,

(F3) Ø(A Ù B) = ØA Ú ØB, Ø(A Ú B) = ØA Ù ØB,

(F4) A Ù (B Ú C) = (A Ù B) Ú (A Ù C), A Ú (B Ù C) = (A Ú B) Ù (A Ú C),

(F5) ØØA = A,

для всех A, B, C Î F.

Нечёткой интерпретацией называется произвольная функция 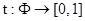, такая, что

t(0) = 0, t(1) =1, t(f Ù g) = min (t(f), t(g)),

t(f Ú g) = max (t(f), t(g)), t(Øf) = 1 – t(f).

Любая функция 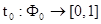может быть единственным образом расширена до некоторой интерпретации .

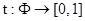Формула f Î F называется нечётко общезначимой, если для любой нечёткой интерпретации t верно неравенство t(f) ³ 0.5. Формула f Î F называется нечётко противоречивой, если для любой нечёткой интерпретации t верно неравенство: t(f) £ 0.5.

Например, формула 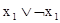нечётко общезначима, а 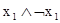– нечётко противоречива.

Теорема 1. Формула f Î F нечётко общезначима тогда и только тогда, когда
f – тавтология в исчислении высказываний K. Формула f Î F нечётко противоречива тогда только тогда, когда она невыполнима в K.

Литералом называется переменная 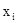или её отрицание 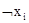. Конъюнкция литералов называется конъюнктом, дизъюнкция литералов – дизъюнктом.

Например: 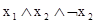– конъюнкт, 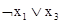– дизъюнкт.

Формула f Î F называется дизъюнктивной нормальной формой (ДНФ), если 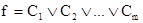для некоторых конъюнктов 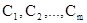. Аналогично конъюнкция 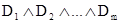дизъюнктов 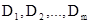называется конъюнктивной нормальной формой (КНФ).

Аксиомы пропозициональной нечёткой логики позволяют переводить любую формулу в ДНФ и в КНФ, в которых не участвуют константы 0 и 1.

Нечёткой импликацией fÞg называется бинарное отношение на F, означающее, что для любой нечёткой интерпретации 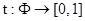верно неравенство t(f) £ t(g).

Принцип резолюции

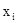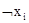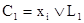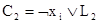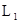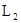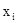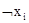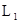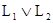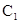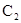Формула f называется содержащей дополнительные переменные, если в ней участвуют литералы и для некоторого i Î w. Пусть и – такие высказывания, что и не содержат ни , ни в качестве сомножителя, и каждое из и не содержит дополнительных переменных. Тогда называется резольвентой и с ключевым словом 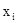и обозначается: 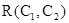. В обычной логике принцип резолюции:

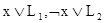
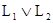
можно применять для доказательства теорем. Следующий пример показывает, что нечёткая импликация:

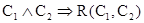
не всегда верна.

Пример

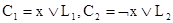. Предположим, что при некоторой интерпретации
t(x) = 0.3, t( 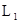) = 0.1, t( 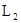) = 0.2. Тогда t( 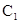) = 0.3, t( 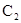) = 0.7. Следовательно, t( 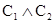) = 0.3. С другой стороны, 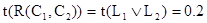, и, значит, 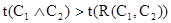. Тем не менее, в некоторых случаях этот принцип применять можно.

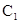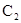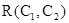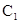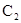Теорема 2. Пусть и – высказывания, – резольвента и с ключевым словом 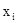. Тогда справедливы утверждения:

1) если 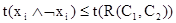, то ;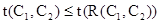

2) если 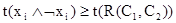, то .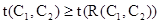

В частности, если 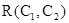нечётко общезначима в том смысле, ч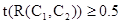то , то 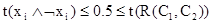, и значит .

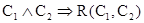5.5. Вывод с нечёткими посылками

При дедуктивном выводе можно применять два правила вывода. Первое из них мы уже рассматривали, а второе выражает принцип доказательства от противного:

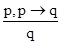(Modus Ponens), 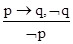(Modus Tollens).

Рассмотрим применение этих правил для нечёткого дедуктивного вывода.

Нечёткие переменные

Пусть U – множество, A Í U – подмножество, элементы которого выделяются с помощью некоторого свойства, определяемого с помощью характеристической функции 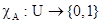. Тогда высказывание: «X принимает значения во множестве A» – означает, что переменная X пробегает значения из U, и это высказывание будет принимать значения, равные 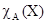. Это высказывание записывается: «X есть A», например, если U = w, а A – подмножество чётных чисел, то запись: «X есть чётное число» будет равносильна X Î A.

Нечёткая переменная определяется как пара, состоящая из символа переменной X, принимающей значения в U, и некоторого множества A, заданного с помощью функции 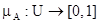. Эта пара записывается: «X есть A». На обычном языке X будет именем элементов универсума, а A – нечётким свойством. Например, «температура нормальная» содержит переменную «температура», принимающую значения в универсуме температур, а «нормальная» будет их нечётким свойством.

Рассмотрим множество составных высказываний, образованных из высказываний: «X есть A» с помощью союзов «и», «или», и связок «если…, то…», «не» – следующим образом:

1) «X есть A и Y есть B» равносильно «(X, Y) есть A Ç B», с 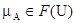, , 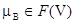где A Ç B – нечёткое множество на U ´ V с функцией принадлежности ;

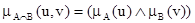2) «X есть A или Y есть B» равносильно «(X, Y) есть A È B», где ;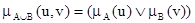

3) «если X есть A, то Y есть B» равносильно «(X, Y) есть A ® B», где ;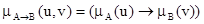

4) «X не есть A» равносильно «X есть не A», где .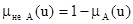

Правила нечёткого вывода

Пусть 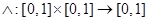– треугольная форма, и пусть импликация связана с ней следующим образом:

.

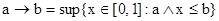Например, если a Ù b = min(a, b), то a ® b будет импликацией Геделя. Для треугольной нормы Лукасевича 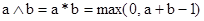импликация определяется как .

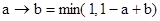Обобщённое правило Modus Ponens было предложено Л. Заде. Пусть заданы нечёткие множества A, B, A¢ с помощью функций: 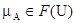, , 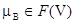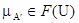. Тогда будет справедливо правило вывода:

Если X есть A, то Y есть B

,

где нечёткое множество B¢ определяется функцией 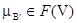, принимающей значения: .

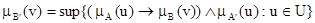Нечеткое множество B¢ можно записать также, пользуясь аналогией с произведением матриц 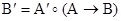,и записать B¢ и A¢, как строки (вместо сложения участвует операция sup, вместо умножения – треугольная норма).

Аналогично для нечётких множеств A, B, B¢, заданных с помощью функций 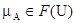, , 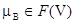, 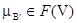обобщённое правило Modus Tollens определяется следующим образом:

Если X есть A, то Y есть B

.

Это правило выражается с помощью равенства:

,

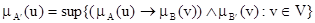если импликация удовлетворяет закону контрапозиции 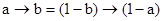. Это верно, например, для треугольной формы Лукасевича и связанной с ней импликацией.

4. Теории первого порядка......................................................................................................................................... 26

4.1. Термы и предикаты......................................................................................................................................................... 26

4.2. Язык логики предикатов.................................................................................................................................................. 29

4.3. Семантика языка логики предикатов............................................................................................................................... 32

4.4. Модели теории первого порядка.................................................................................................................................... 34

4.5. Компактность и полнота языка первого порядка........................................................................................................... 36

4.6. Упрощение формул........................................................................................................................................................ 38

4.7. Метод резолюций Робинсона......................................................................................................................................... 39

5. нечеткая логика.......................................................................................................................................................... 41

5.1. Нечеткие множества........................................................................................................................................................ 41

5.2. Логические операции...................................................................................................................................................... 43

5.3. Нечеткие отношения....................................................................................................................................................... 45

5.4. Пропозициональная нечеткая логика............................................................................................................................. 46

5.5. Вывод с нечёткими посылками....................................................................................................................................... 47