Тождественные преобразования

Как видно на рис.4.4 и рис.4.5, одна и та же булева функция может быть реализована различными переключательными схемами и описана разными формулами. Далее рассмотрим правила тождественного преобразования булевых функций.

На основании таблиц соответствия нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры:

1) коммутативность:

;

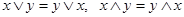2) ассоциативность:

;

3) дистрибутивность:

;

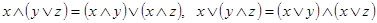4) свойство констант:

;

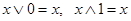5) свойство отрицания:

.

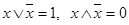Рассмотрим для примера доказательство первого из законов дистрибутивности с помощью таблицы соответствия. Для этого построим таблицы соответствия для левой и правой частей предполагаемого тождества (см.табл.5.1).

Таблица 5.1
х	у	z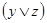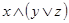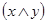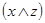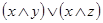

Как видно из табл.5.1, значения левой и правой части (выделены жирным шрифтом) совпадают при всех значениях переменных, что и требовалось доказать.

Аналогично, путем построения таблиц соответствия, могут быть доказаны и другие приведенные выше тождества.

Эти свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия:

1) законы де Моргана:

;

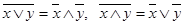2) законы поглощения:

;

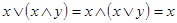3) законы идемпотентности:

.

Докажем справедливость первого из законов де Моргана. Для этого равенство 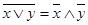путем последовательных преобразований сведем к очевидному тождеству.

Из равенства 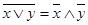и свойств отрицания следует, что

т.е.

После раскрытия скобок получим следующее:

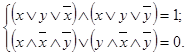
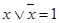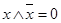Так как и , а и 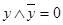, то предыдущее выражение можно представить в следующем виде:

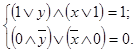
Используя свойства констант ( 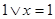, , 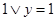, 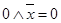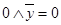), получаем

– очевидное тождество.

Таким образом, путем эквивалентных преобразований мы привели выражение первого закона де Моргана к тождеству и этим доказали справедливость данного закона.

Второй закон де Моргана может быть легко получен на основе первого путем отрицания левой и правой части и соответствующей замены переменных. Запишем первый закон де Моргана относительно переменных a и b:

.

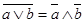Если равны сами выражения, то равны и их отрицания:

.

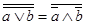Из свойств двойного отрицания:

.

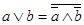Произведем замену переменных:

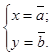
После замены получим:

,

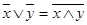т.е. второй из законов де Моргана.

Также имеют место следующие тождества:

; ;

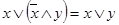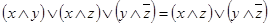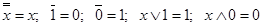и т.д.

Вопросы и задания

5.1. Докажите с помощью таблицы соответствия справедливость законов ассоциативности и поглощения.

5.2. Путем последовательных преобразований проверьте, какие из следующих выражений являются верными тождествами:

а) ;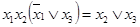

б) ;

в) .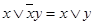

Сравните полученные результаты с результатами задания 3.15.