Необходимые и достаточные условия

1.Докажите теорему об основных правилах логического вывода (см. приложение 3).

2.Придумайте не менее трёх своих правил логического вывода и убедитесь, что они следуют из основных правил (см. приложение 3).

3.Проанализируйте основные правила логического вывода и найдите несколько правил, которые следуют из других.

4.Проверьте двумя способами, есть ли логическое следование:

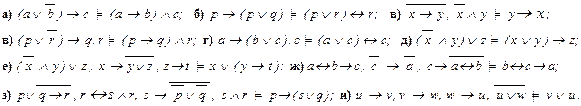
5.Правильны ли следующие рассуждения ?

а) Если Анна знает алгебру, то она умеет решать алгебраические уравнения. Анна умеет решать алгебраические уравнения. Следовательно, Анна знает алгебру.

б) Если будет хорошая погода, мы пойдем в лес или купаться на речку. Мы не пошли ни в лес, ни на речку. Следовательно, погода испортилась.

в) Если я сдам ЕГЭ по математике на “отлично”, я поступлю в МГУ на мехмат. Я не сдал ЕГЭ на “отлично”, следовательно, я не поступлю в МГУ на мехмат.

г)з) Если мне купят “мерс”, то я поеду в институт. Если я сдам сессию хорошо, то поеду на Канары. Мне не купили “мерс”. Поэтому либо я не поеду на Канары, либо не поеду в институт.

д)Если я пойду завтра на первую пару, то буду должен рано встать. Если я пойду на дискотеку, то лягу спать поздно. Если я лягу поздно или встану рано, то буду спать не более 5 часов. Следовательно, если я буду спать не более 5 часов, то я должен пропустить завтра первую пару и пойти на дискотеку.

е) Если 6 составное число, то 12 – тоже составное. Если 12 – составное, то найдётся простое число, большее 12. Если существует простое, большее 12, то существует и составное, большее 12. Если 6 делится на 2, то 6 – составное. Число 12 – составное. Значит, 6 – составное число.

ж) Если будет холодно, то она наденет тёплое пальто, если рукав будет починен. Завтра будет холодно, и она наденет пальто, но рукав починен не будет. Значит, она не наденет тёплое пальто, или рукав будет починен.

з) 2 ¹ 5 и 6 £ 7. Если 2 = 5, то 6 > 7 при условии что 4 < 3. Ясно, что 3 £ 4 и 2 ¹ 5. Значит, из того, что 6 £ 7 не следует, что 2 = 5.

и) Если наступит весна, то распустятся цветы. Если цветы распустятся, то прилетят пчёлы в том случае, если их не спугнут шершни. Шершни спугнули пчёл. Значит, даже если наступит весна, то цветы не распустятся.

6.Проанализируйте следующее рассуждение: “Если 2 = 2, то 1 = 1. Значит, 3 = 3.“ Убедитесь, что оно неправильное с точки зрения логики. В то же время, с точки зрения математики в целом все утверждения в этом рассуждении истинны ! Как объяснить этот “парадокс” ?

7.Докажите следующие правила логического вывода:

а) A₁ Ú … Ú A_n , A₁ ® B, … , A_n ® B 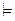B;

б) A₁ ® A₂ , A₂ ® A₃ , … , A_n–1 ® A_n 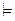A₁ ® A_n ;

в) ;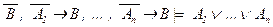

г) A₁ ® (A₂ ® (A₃ ® ( … ® (A_n–2 ® (A_n–1 ® A_n)) … ))), .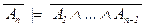

8.Докажите, построив примеры формул F и G, что из утверждения “если 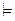F, то 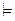G” не всегда следует “F 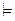G”.

9.Верно ли, что из “если 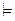F, то 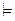G ” следует, что “если 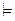F Ù H, то 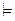G Ù H ” для любой формулы H ?

10.Верно ли, что из “F 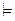G ” следует, “ FÙ H 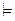G Ù H ” для любой формулы H ?

11.Что можно сказать о формуле G, если

а) F 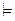G и F º 0; б) G 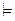F и F º 1; в) F Ù G 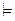G Ù 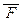для некоторой формулы F; г) F Ù G 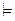G Ù 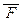для любой формулы F; д) F Ú G 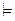G для любой формулы F; е) F, G ® F 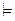F ® G для некоторой формулы F; ж) G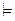 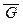; з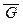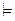) G ® G.

12.Вставьте слова “необходимо, но не достаточно”, “достаточно, но не необходимо”, “необходимо и достаточно”, “не необходимо и не достаточно”, чтобы полученные высказывания стали истинными. Пояснить необходимость вставленных слов.

а) Для делимости числа на 12 … , чтобы оно делилось на 3.

б) Для чётности натурального числа n … , чтобы число 5×n , было чётным.

в) Для делимости числа a×b на с … , чтобы а и b делились на с (a, b, c Î Z).

г) Для того, чтобы х² + у² = 0 … , чтобы х = 0 и у = 0.

д) Для того, чтобы х² – у² = 0 … , чтобы х = 0 и у = 0.

е) Для того, чтобы треугольник был прямоугольным … , чтобы две его стороны были равны.

ж)Чтобы прямая была перпендикулярна плоскости … , чтобы она была какой-либо прямой этой плоскости.

з)Чтобы прямая была перпендикулярна плоскости … , чтобы она была перпендикулярна какой-либо прямой этой плоскости.

и) Для того, чтобы х² = у² … , чтобы х = у.

к)Для того, чтобы х < у …, чтобы |х| < |у|.

л)Для того, чтобы х² – 5×х + 6 = 0 … , чтобы х = 3.

м)Для того, чтобы сумма чётного числа натуральных чисел была чётным числом, … , чтобы каждое слагаемое было чётным.

н)Для того, чтобы окружность можно было вписать в четы­рёх­угольник, … , чтобы суммы длин его противоположных сторон были равны.

13.Для каждого из следующих условий выясните, является ли оно необходимым и является ли оно достаточным для того, чтобы выполнялось неравенство х² – 2×х – 8 £ 0.

а) х = 0,б) х ³ –3,в) х > – 2,

г) х ³ – 1 и х £ 3, д) х ³ – 1 и х < 10, е) – 2 £ х £ 10.

14.Решите предыдущее упражнение для неравенств x² – 5×x + 9 ³ 0 и x² – 5×x + 9 < 0.

15.Выясните, какое из двух неравенств является следствием другого:

а) x ³ 0, x > 7, б) x + 8 > 0, x > –8, в) x + 2 > –1, x < 15,

г) x² ³ 0, x > 0, д) x×(x + 1) > 0, x×(x – 3) > 0, е) |x² + x| > 0, x² > 9,

ж) x² + 5×x – 6 > 0, x > 8, з) |x² + 6×x – 6| > 0, x² + 6×|x| – 8 > 0, и) 1 £ |x| < 1, x² < 8.

16.Для каждого из следующих утверждений составьте обратные, противоположные и контрапозиционные. Какие из полученных утверждений Вы можете доказать, а какие – опровергнуть ?

а) если р – нечётное простое число, то р² – 1 делится на 8,

б) сумма квадратов диагоналей ромба равна сумме произведений противоположных его сторон,

в) если а, b, c – длины сторон прямоугольного треугольника, то c² = (a + b)² – 2× ,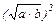

г) если хорды окружности делят друг друга пополам, то они – диаметры,

д) сумма векторов, с началом в центре правильного n-угольника и концами в его вершинах равна нулевому вектору,

е) при любом x Î Rвыполнено 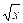> x.