Отношения между суждениями

ПО ИСТИННОСТИ.

«ЛОГИЧЕСКИЙ КВАДРАТ»

Зная структуру простых и сложных суждений, учитывая их истинностные характеристики (значения) для тех или иных условий, можно установить определённые формальные отношения между ними. Последнее имеет важное значение для характеристики процессов рассуждения, выводов из одних суждений других, что потребуется нам в разделе «Умозаключение».

Первый вид отношений, с которого начинается переход к чисто формальным отношениям суждений, связан с отношением сравнимости (несравнимости) суждений по содержанию.

Сравнимыми суждениями (отношение сравнимости) — называются суждения, которые состоят из одних и тех же содержательных элементов. Для простых суждений это значит, что они состоят из одних и тех же понятий, которые выступают их субъектами и предикатами. Простые суждения при этом могут отличаться друг от друга кванторами, качеством связок, расположением понятий (на месте субъекта или предиката). Например, сравнимыми будут суждения: «Некоторые города являются столицами своих стран» — «Все столицы являются городами».

Сравнимые сложные суждения — это такие суждения, которые состоят из одних и тех же простых суждения, взятых в любом порядке. Кроме этого, сложные суждения могут различаться наличием различных связок, логических союзов, наличием или отсутствием отрицаний простых или сложных суждений. Так, если обратиться к таблице на Рис. 14, то можно говорить, что сравнимыми являются все суждения, форма которых совпадает хотя бы с одной из указанных в таблице.

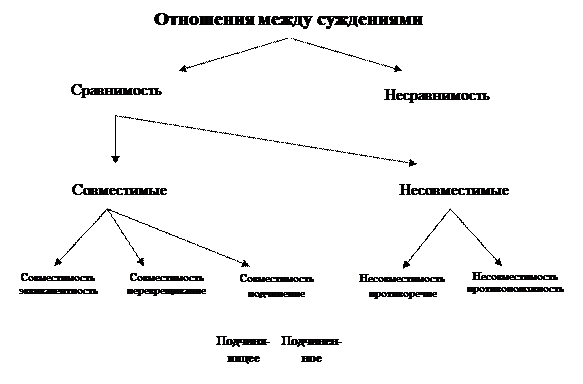
Суждения, у которых имеется хотя бы один не общий содержательный элемент, называются несравнимыми, их сравнение по форме на этом заканчивается (см. Рис. 16).

Отношение сравнимости подразделяется на сравнимость-совместимость и сравнимость-несовместимость. Здесь учитывается, помимо сравнимости по содержательным элементам, соотношение суждений по истинности для всех возможных случаев.

Сравнимость-совместимость— это такое отношение, при котором суждения могут быть одновременно (хотя бы в одном случае, в одной строке) истинными.

Сравнимость-несовместимость — это такое отношение, при котором сравниваемые суждения не могут быть одновременно истинными для всех наборов их истинностных значений.

Различают три основных разновидности совместимости и две основных разновидности несовместимости (см. Рис. 16).

Совместимость-эквивалентность — это такая совместимость, при которой сравнимые суждения имеют в одних и тех же случаях значение «И» и в одних и тех же случая — значение «Л». На рис. 16 в соответствующей табличке отсутствуют строки значений : «ИЛ» и «ЛИ».

Совместимость-перекрещивание — это отношение между сравнимыми суждениями, которое характеризуется тем, что суждения могут быть одновременно истинными, могут иметь взаимно противоположные значения («ИЛ» и «ЛИ»), но не могут быть одновременно ложными. Это, например, отношение между двумя частными суждениями противоположного качества — частноутвердительными и частно-отрицательными простыми категорическим суждениями.

А В А В А В А В А А

И И И И И И

И Л И Л И Л

Л И Л И Л И Л И

Л Л Л Л Л Л

Рис. 16

Примечание: на схеме Рис. 16 в наборах истинностных значений для различных видов отношений между суждениями оставлены только те, которые допустимы, т.е. могут встречаться для этих отношений, о чем говорят определения соответствующих видов отношений.

Совместимость-подчинение — это отношение сравнимости, при котором, если одно из суждений, являющееся подчиняющим (А), истин­но, то другое суждение, являющееся подчиненным, должно быть обя­зательно истинным. И не может быть обратного случая, при котором подчиненное суждение ложно, а подчиняющее истинно. Это, например, отношение между общим (подчиняющее) и частным (подчиненное) суждением одного качества (А и I, Еи О). В соответ­ствующей табличке на рис. 16 отсутствует строка «ЛЛ».

Несовместимость-противоречие, или формальная несовме­стимость (контрадикторность) — это такое отношение сравнимос­ти-несовместимости, при котором суждения не могут быть как од­новременно истинными, так и одновременно ложными, а могут иметь только противоположные значения: «ИЛ» или «ЛИ». Например, отношение между общими и частными суждениями про­тивоположного качества: А и О, Е и I. Это также отношение, которое имеет место между суж­дением и его формальным отрицанием: А и А.

Несовместимость-противоположность, или содержательная не совместимость (контрарность) — несовместимость между сравнимыми суждениями, которые не могут быть одновременно истинными, но могут быть одновременно ложными. Например, суждения, утверждающие наличие различных признаков, несовместимых по своей природе, у одного и того же предмета, например: «быть белым» — «быть черным», «быть прокурором» — «быть адвокатом» и т.п.

Заметим, что формальная логика не несет ответственности за установление несовместимости в отношении содержания при­знаков. Содержательная несовместимость устанавливается в соответствующей предметной области, в отношении которой логиков нельзя считать специалистами.

Так, считавшаяся ранее несовместимой характеристика «быть частицей» в отношении характеристики «быть волной», оказалась со­вместимой со второй. Ло­гика всегда с полным правом отмечала неправильность выражения: «Электрон — частица и электрон — не частица», настаивая на его ложности, поскольку в нем присутствует формальная несовместимость суждении. То же самое относится и к выражению: «Электрон — волна и не волна». Что касается истинности (ложности) суждения: «Электрон — частица и электрон — волна», которое большинство физиков поначалу посчитали ложным, то это вовсе не вытекало из требований логики самих по себе. Требова­ния логики действуют только в отношении признаков, несовместимость которых установлена конкретными исследователями, в данном случае физиками. Это сами физики посчитали, что признаки частицы и волны несовместимы, и на этом основании прибегали к требова­ние логики, запрещающему их одновременную истинность. Впоследствии сами же физики изменили свою точку зрения и данные признаки перестали считаться несовместимыми в отношении микрочастиц.

В традиционной формальной логике уже давно, еще со времен схоластов, учитываются отношения между суждениями по истин­ности дляпростых категорических суждений. Ими был придуман «логический квадрат» (см. Рис. 17):

Рис. 17

На этой схеме видно, какие отношения между простыми категорическими суждениями имеют место:

1) общеутвердительные (А) и общеотрицательные (Е) — отношение несовместимости-противоположности (могут быть одновременно ложными, но не могут быть одновременно истинными);

2) общеутвердительные (А) и частноотрицательные (О) — отношение несовместимости-противоречия (не могут быть ни одновременно истинными, ни одновременно ложными). То же самое имеет место между общеотрицательными и частноутвердительными сравнимыми суждениями;

3) общеутвердительные (А) и частноутвердительные (I) — отношение совместимости-подчинения, причем подчиняющим является общее суждение, а частное — подчиненным (при истинности общего частное обязательно истинно, но не наоборот: частное может быть как истинным, так и ложным при ложности общего). То же самое имеет место между общеотрицательными и частноотрицательными;

4) частноутвердительные (I) и частноотрицательные (О) – отношение совместимости-перекрещивания (могут быть одновременно истинными, могут иметь противоположные значения, но не могут быть одновременно ложными). Это отношение еще называют «подпротивоположностью» или «субконтрарностыо».

Знакомство с «логическим квадратом» существенно облегчает оперирование простыми категорическими суждениями, особенно с целью их простейших непосредственных преобразований (см. непосредственные умозаключения, глава 3, раздела VI).

Глава 5.