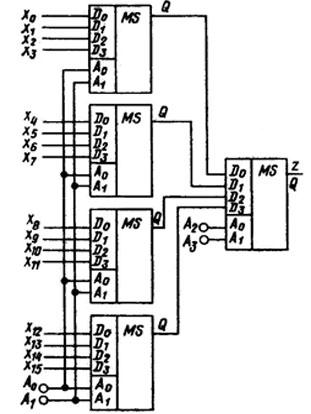
При передаче информации от нескольких источников по общему каналу с разделением по времени нужны не только мультиплексоры, но и устройства обратного назначения, распределяющие информацию, полученную из одного канала между несколькими приемниками. Эту задачу решают демультиплексоры.
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
23. Минимизация логических функции методом карт Вейча
Карта Вейча – это определенным образом заполненная таблица истинности логической функции.
В клетки карты Вейча записывают значения функции. Положение клетки определяется набором аргументов.
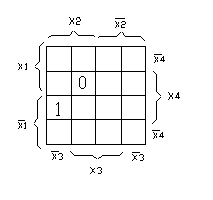
Фигурные скобки показывают части карты, где аргументы X1, X2, X3, X4 равны «лог.1» или «лог. 0».`
Необходимо учесть, что X1, X2, X3, X4 = 1, а 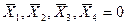
Например: f (1, 1, 1, 1) = 0, f (0, 1, 0, 1) = 1 (рисунок 1)
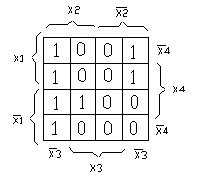
Рисунок 1
Процесс минимизации осуществляется в 3 этапа:
1) Заполнить карту Вейча в соответствии с функцией заданной таблицей. Пусть «0» и «1» в карте Вейча расположились так, как показано на рисунке 2.
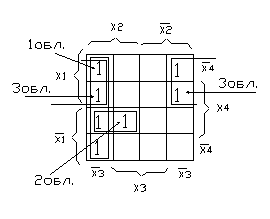
Рисунок 2
2) Чтобы получить МНДНФ необходимо: единицы объединить в области вдоль строк и вдоль столбцов, так чтобы в область входило 2
n клеток, при этом стремятся, чтобы количество областей было минимальным, а количество клеток, входящих в область было максимальным. Допускается пересечение областей, клетки, находящиеся на краях карты Вейча, можно объединять в области, сворачивая карту в цилиндр.
3) Для каждой области записать выражение в МДНФ, в которое входят аргументы, не меняющие внутри области свое значение с инверсного на не инверсное (рисунок 3)/
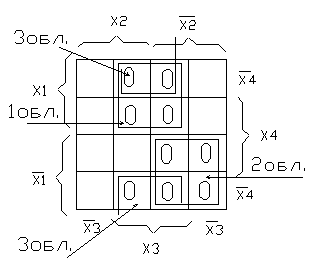
Рисунок 3.
МДНФ 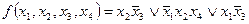
Чтобы получить МКНФ необходимо по такому же правилу в области объединить 0, но при записи аргументов их дополнительно инвертировать (4.)

Рисунок 4.
МКНФ 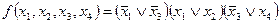
| Синякина Г.Е. МММММММММММММММммухамедшиной. |
24. Минимизация логических функций методом Квайна
Метод Квайна позволяет представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах.
Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе - переход от сокращенной формы логического выражения к минимальной форме.
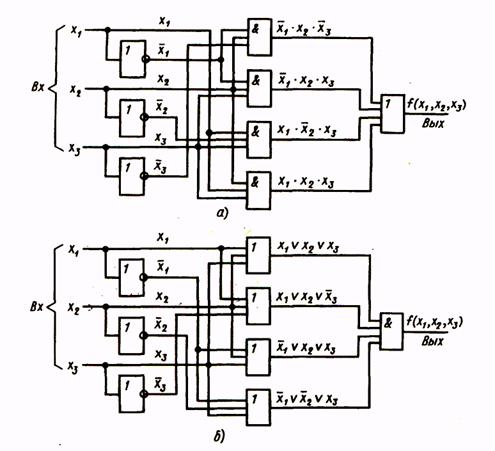
Рис. 1
Первый этап (получение сокращенной формы). Пусть заданная функция представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.
Для выполнения операции склеивания в выражении функции выявляются пары членов вида 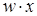 и
и 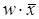 , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов:
, различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов: 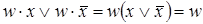 , и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве
, и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве 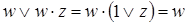 (член w поглощает член
(член w поглощает член 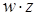 ). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
Операции склеивания и поглощения выполняются последовательно до тех пор, пока это возможно. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции, заданной в табл. 2.
Таблица 2

Совершенная ДНФ этой функции
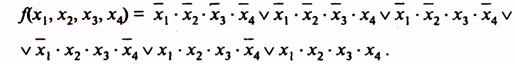 (3)
(3)
Для получения сокращенной формы проводим операции склеивания и поглощения:
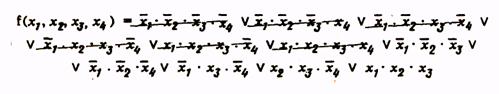 (4)
(4)


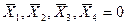



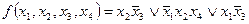

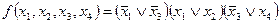

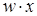 и
и 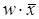 , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов:
, различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар членов: 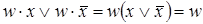 , и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве
, и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве 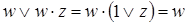 (член w поглощает член
(член w поглощает член 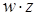 ). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции склеивания.
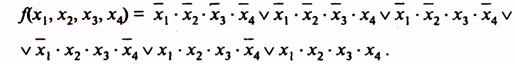 (3)
(3)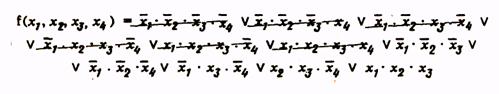 (4)
(4)