Логические и арифметические основы и принципы работы ЭВМ

Инверсия

Читается НЕ Х или Х с чертой, отрицание Х.

Возьмем, например, такое высказывание: А=<Киев-столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т.е. не верно, что <Киев-столица Франции>.

Из простых высказываний можно строить более сложные, применяя так называемые связи.

Логические связи – это ФАЛ, аргументами которых являются простые высказывания.

Конъюнкция Возьмем 2 высказывания: А=<Москва – столица РФ> В=<дважды два - четыре> тогда сложное высказывание: А & В будет истинным, так как истинны оба этих высказывания. Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если истинному высказыванию приписать значение '1', а ложному - '0', то сложное высказывание можно назвать произведением.

X1	X2	f1(X1,X2)

Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.

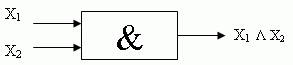
Дизъюнкция

Это сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.

X1	X2	f1(X1,X2)

Читается X1 ИЛИ X2: Некоторое отличие от смысла союза «или», принятого в русском языке: в данном случае этот союз употребляется в смысле объединения, а не разъединения.

Логическая равнозначность

Это сложное высказывание истинно тогда, когда истинны или ложны одновременно оба высказывания.

Отсюда следует, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания.

Например,

А=<дважды два - пять>

B=<один плюс два - шесть>

А~В равнозначны.

Импликация

Это сложное высказывание ложно только тогда, когда X1 – истинно, а X2 – ложно.

X1	X2	f1(X1,X2)

Читается: если X1, то X2. При этом X1 – посылка, X2 – следствие.

Если посмотреть на таблицу истинности, то может показаться странным название этой функции, т.к. из него следует, что истинным может быть высказывание, составленное из двух ложных.

Но в действительности, все верно, т.к. содержанием высказываний в алгебре логики не интересуются.

Тогда из ложной посылки может следовать ложное следствие и это можно считать верным:

<если Киев – столица Франции>,

то <2-квадрат 3>.

Эквивалентности

В некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.

Дизъюнкция:

х х х х... х х х= х ,

т.е. истинность высказывания не изменится, если его заменить более коротким, таким образом, это правило приведения подобных членов:

x v x = 1

1 x = 1

– постоянно истинное высказывание.

0 x = x

x1 x2 = x2 x1

- (переместительный) коммуникативный закон.

x1 х2 х3 = (x1 х2) х3 = x1 (х2 х3)

- сочетательный закон.

Конъюнкция:

х х х х... х х х= х

правило приведения подобных членов:

1 x = х

0 x = 0 - постоянно ложное высказывание

x x = 0 - постоянно ложное высказывание

Сложение по mod 2

1 х = x

0 x = x

x x = 1

x x x ... x = х – при нечетном числе членов, 0 - при четном числе членов

Правило де Моргана

x1 x2 ... xn = x1 & x2& ... & xn

x1 x2 ... xn = x1 & x2 & ... & xn

Докажем для двух переменных с помощью таблицы истинности:

Х1	Х2	Х1 Х2	X1 & X2

Операция поглощения:

Х XY = X или в общем виде X X*f(X,Y,Z...) = X;

Операция полного склеивания:

XY XY = X (по Y)

XY XY = Y (по Х)

Операция неполного склеивания:

XY XY = Х XY XY

В лекции дано определение совершенной дизъюнктивной и конъюнктивной нормальных форм. Представлены правила записи функции по нулям и единицам. Дано понятие функциональной полноты, поставлена задача минимизации функции. Сформулирована теорема Квайна.

Введем понятие степени:

Х

=Х, если =1;

=Х, если =0.

Рассмотрим конъюнкцию вида:

Х1 1 * Х2 2 * Х3 3 ... Хn n

Существует 2n наборов вида < 1, 2, ... n >. Поставим в соответствие каждой конъюнкции (*) номер набора i и образуем дизъюнкцию всех конъюнкций:

i A(Х1 1 * Х2 2 * Х3 3 ... Хn n )

Теорема (без доказательства):

Любая ФАЛ, зависящая от 'n' аргументов, может быть представлена в форме:

F(Х1, Х2,... Хi... Хn)= Х1 1 * Х2 2... Хi i F( 1, 2, ... i, Xi+1,...Xn)

Из этой теоремы вытекает ряд важных следствий:

1. Она дает возможность перейти от табличного задания функции к аналитической форме и сделать обратный переход.

2. Устанавливает так называемую функциональную полноту связок (базиса) " , , -", т.к. позволит построить в этом базисе произвольную ФАЛ от произвольного числа аргументов.

Примечание:

1. Если i n, то соответствующая форма функции называется дизъюнктивной нормальной (ДНФ).

2. Если i=n, то каноническая форма функции носит название совершенной ДНФ (СДНФ). Дизъюнкции берутся по тем наборам, на которых функция f(X1,X2,...,Xn)=1

Пример: ДНФ

f(Х1, Х2, Х3)= Х1 Х2 Х3 Х1Х2 Х3

Пример: СДНФ

f(Х1, Х2, Х3)= Х1Х2 Х3 Х1Х2 Х3

В ДНФ в каждый член любая переменная входит в прямом виде или с отрицанием.

Аналогичная теорема справедлива и для представления функции в конъюктивной нормальной форме (КНФ):

f(Х1, Х2,..., Хn)=&( Х1 1 Х2 2 ... Хi i) f( 1, 2, ... i, Xi+1...Xn)

или при представлении в совершенной КНФ (СКНФ):

f(Х1, Х2,…, Хn)=&( Х1 1 Х2 2 Х3 3 ... Хn n)

где: & означает, что конъюнкции берется по тем наборам, на которых

f(Х1, Х2, ... Хn)=0.

Дадим на основании этих теорем правило перехода от табличной формы функции к СДНФ и СКНФ.

Переход от табличной формы функции к СДНФ или правило записи функции по единицам:

1. Выбрать те наборы аргументов, на которых f(Х1, Х2, ... Хn)=1.

2. Выписать все конъюнкции для этих наборов. Если при этом Хi имеет значение '1', то этот множитель пишется в прямом виде, если '0', то с отрицанием.

3. Все конъюнктивные члены соединить знаком дизъюнкции .

Пример:

f(Х1, Х2)= Х1Х2 Х1Х2 Х1Х2

X1	Х2	f(Х1, Х2)

Правило перехода от табличной формы задания функции к СКНФ или правило записи функции по нулям.

1. Выбрать те наборы аргументов, на которых f(Х1, Х2, ... Хn)=0.

2. Если при этом Хi имеет значение '0', то остается без изменений. Если '1', то с отрицанием.

3. Все дизъюнктивные члены соединить знаком конъюнкции .

Пример:

f(Х1, Х2)= (Х1 Х2) ( Х1 Х2 )

X1	Х2	f(Х1, Х2)

Пример:

X1	Х2	Х3	f(Х1, Х2, Х3)

СДНФ f(Х1, Х2, Х3)= Х1Х2Х3 Х1Х2Х3 Х1Х2Х3 Х1Х2Х3 Х1Х2Х3

СКНФ f(Х1, Х2, Х3)= (Х1 Х2 Х3) & (Х1 Х2 Х3) & (Х1 Х2 Х3)

Рассмотрим способ получения СДНФ из СКНФ и обратно.

Из таблицы 2.1 с помощью способа записи функции по нулям следует, что СКНФ той же функции дизъюнкции будет иметь вид:

f(Х1, Х2)= Х1 Х2

X1	Х2	f(Х1, Х2)

Итак, имеем две формы одной и той же функции:

f(Х1, Х2)= Х1Х2 Х1Х2 Х1Х2 =Х1 Х2

Итак, видно, что общее число членов в этих двух формах равно сумме нулей и единиц функции, то есть равно 2n.

Если в исходной форме функции, записанной в СКНФ или СДНФ, содержится z членов, то в другой ее форме (т.е. СДНФ или СКНФ) их будет (2n- z).

Поскольку в функцию мы включаем дизъюнктивные или конъюнктивные члены и берем их по наборам, на которых функция или обращается в '0', или в '1', то для перехода от одной формы задания функции к другой нужно выписать все недостающие члены и поставить над каждой переменной отрицание, а также заменить знаки конъюнкции на дизъюнкцию и обратно.

f(Х1, Х2)= Х1 Х2

f(Х1, Х2)СДНФ= Х1Х2 Х1Х2 Х1Х2

т.е. получили СДНФ.

Практический смысл перехода заключается в том, что можно определить, реализация какой формы потребует меньший объем оборудования.

Понятие функциональной полноты ФАЛ Было отмечено, что техническая (физическая) задача синтеза произвольного устройства сводится к математической задаче построения произвольной ФАЛ. Естественно возникает вопрос, какое количество связок необходимо, чтобы построить произвольную ФАЛ. Ответ на этот вопрос не однозначен. Мы видим, что, например, с помощью только функции f0 (константа 0), f15 (константа 1) произвольную ФАЛ построить нельзя. Нельзя ее построить и с помощью только инвертора. Существуют и другие базисы: , , 1, |. Есть также одноэлементные базисы: f8 – стрелка Пирса, f14 – штрих Шеффера, И-НЕ, ИЛИ-НЕ. Технически синтез устройства означает, что нужно иметь некоторый набор элементов, ФАЛ которых образуют базис, чтобы можно было построить реальное устройство. Однако, как было отмечено, задача синтеза ФАЛ – идеальная модель. В действительности, для построения реальных устройств пользуются несколько более расширенным набором элементов - усиления и коррекции сигналов. Минимизация ФАЛ и ограничения при ее рассмотрении Покажем на примере, что СДНФ не является экономной формой записи: f(Х1, Х2)= Х1Х2 Х1Х2 Х1Х2 =Х1 Х1 Х2 на основании полного склеивания по Х2 мы видим, что запись стала короче, т.к. содержит меньшее число связок и букв. Физически это означает, что устройство, которое реализует эквивалентную, но более простую функцию, будет иметь в своем составе меньшее количество оборудования, а следовательно, будет работать надежнее. Итак, задача синтеза устройства должна быть дополнена задачей уменьшения оборудования в нем. С математической точки зрения это задача построения минимальной ФАЛ. Под минимальной ФАЛ понимается такая форма, в которой содержится меньшее количество букв и членов, чем в ее исходной форме. Речь идет именно о буквах, а не о переменных, так в функции: f(Х1, Х2)= Х1Х2 Х1Х2 Х1Х2 имеется 6 букв и только 2 переменных. Видно, что если какое-либо элементарное произведение входит в функцию, то при добавлении к нему новых сомножителей, полученное произведение так же будет входить в функцию. Пример: если Х1Х2 входит в функцию от любого числа аргументов (>2), то в нее войдет, например, произведение Х1Х2Х3. Это можно показать так: f(Х1, Х2)= Х1Х2 (Х1Х2)= Х1Х2 (Х3 Х3) (Х1Х2)= Х1 Х2 Х3 Х1 Х2 Х3 (Х1Х2)=Х1 Х2 Х3 (Х1 Х2 Х3) Дадим ряд определений: 1. Произведение одной или нескольких неповторяющихся переменных, взятых с отрицанием или без него, называют элементарным. Например, Х1 Х2 Х3 – элементарное произведение, т.к. в него входят различные буквы Х1 Х2 Х3. 2. Дизъюнкция элементарных произведений – ДНФ. 3. ДНФ является минимальной, если в ней минимальное число букв и членов. 4. Конституентой единицы функции называют функцию, принимающую значение единицы только на одном наборе аргументов. Обычно конституенты единицы выражают через произведение всех переменных, от которых зависит функция. СДНФ – дизъюнкция конституент единицы. 5. Ранг произведения – число букв, входящих в него. 6. Собственной частью называется произведение, полученное путем отбрасывания одной или нескольких переменных. Например, Х1 Х2 Х3 Х4, где Х1, Х1 Х2, Х1 Х2 Х3 – некоторые собственные части. 7. Если функция равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что является импликантой функции F (т.е. нулей у импликанты не меньше, чем у функции). 8. Простой импликантой называется произведение, которое само входит в выражение функции, но никакая его собственная часть в выражение функции не входит. Например, Х1 Х1 Х2 Х3 Х1Х3=f: здесь Х1- простая импликанта, а Х1 Х2 Х3 и Х1 Х3 - не простые. Понятие покрытия Определение. Если на каком-либо наборе f принимает значениа а1, а – значение а2, то говорят, что f своим значением а1 покрывает значение а2 функции . При минимизации ФАЛ стремятся получить форму, в которой будет меньше букв, чем в исходной. По отношению к ДНФ эта форма называется сокращенной (Сок. ДНФ). Смысл построения Сок. ДНФ заключается в том, что в нее входят такие элементарные произведения, которые своими единицами покрывают не одну единицу исходной функции, а несколько. Так, каждое элементарное произведение, входящее в СДНФ, покрывает только одну единицу функции. Например: f(Х1, Х2)= Х1Х2 Х1Х2 Х1Х2 1 1 1 Эти единицы функции могут быть накрыты более короткими произведениями: в частности, Х1 накрывает две единицы: Х1Х2 и Х1Х2 и Х2 , которое накрывает также две единицы: Х1Х2 и Х1Х2 , т.е. f(Х1, Х2)= Х1 Х2

ТЕОРЕМА (без док-ва):

Любая ФАЛ может быть представлена единственным образом в Сок. ДНФ, т.е. записана в виде дизъюнкции простыхимпликант.

Сокращенная форма не означает, что это форма является минимальной. Однако для практической реализации эта форма более удобна, чем совершенная.

Рассмотрим метод получения Сок. ДНФ, предложенный Квайном. Этот метод, и, в частности, теорема Квайна в явном и неявном виде входит практически во все методы минимизации.

Исходная форма функции – совершенная ДНФ.

ТЕОРЕМА Квайна:

Если в СДНФ в начале произвести все операции неполного склеивания, а затем все операции поглощения, то в результате получится сокращенная ДНФ.

Покажем, что, применяя операцию неполного склеивания, получим все простые импликанты функции. Введем операцию развертывания, которая обратна операции склеивания: это есть умножение каждого произведения на выражение вида (Х X)=1.

Пусть Х₁Х₂ – простая импликанта некоторой f(Х₁, Х₂, Х₃) трех переменных. Тогда:

Х₁Х₂ (Х₃ Х₃)=Х₁ Х₂ Х₃ Х₁ Х₂ Х₃

получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.

В эту форму, вообще говоря, могут входить несколько одинаковых членов, т.к. разные простые импликанты могут дать одинаковые конституенты единицы. Поэтому, отбросив в ДНФ лишние члены, получим ее СДНФ.

По отношению к СДНФ применяется операция неполного склеивания, т.к. одно и то же произведение, вообще говоря, может склеиваться с несколькими другими, давая различные импликанты, то чтобы не лишиться возможности провести все операции склеивания, приходится каждое произведение, которое участвовало в операции склеивания, оставить для других операций.

Пример:

f(Х₁, Х₂)= Х₁Х₂ Х₁Х₂ Х₁Х₂ = Х₁Х₂ Х₁ или Х₁Х₂ Х₂

Таким образом после выполнения операции неполного склеивания получится не только дизъюнкция простых импликант, но и часть конституент единицы.

Если теперь провести все операции поглощения, то в полученной форме функции f останутся только простые импликанты. Покажем это. Пусть в результате операций склеивания получится член x, не являющийся простой импликантой.

Тогда x=y*z, где z – простая импликанта, которая так же должна входить в f, т.к. в нее входит x. Но z будет поглощать х, поэтому х не может входить в f. Это и доказывает теорему Квайна.

Замечание: Заметим, что теорема Квайна применяется по отношению к функции СДНФ.

Порядок получения Сок. ДНФ может быть следующим:

1. Провести все операции неполного склеивания конституент единицы исходной СДНФ. Получатся произведения (n-1) ранга; оставшиеся несклеенные конституенты единицы не могут участвовать в дальнейших склеиваниях.

2. Провести покрытие всех полученных произведений и конституент единицы. Часть некоторых конституент единицы будет устранена.

3. Продолжить, пока возможны операции 1) и 2).

Пример 1:

f(Х₁, Х₂)= Х₁Х₂ Х₁Х₂ Х₁Х₂

Если применим операцию полного склеивания, то получим:

или

f(Х₁, Х₂)= Х₁ Х₁Х₂

или

f(Х₁, Х₂)= Х₁Х₂ Х₂

т.е. у нас нет возможности далее провести операцию.

Применим теперь операцию неполного склеивания:

f(Х₁, Х₂)= Х₁ Х₁Х₂ Х₁Х₂ Х₁Х₂ Х₂ = Х₁ Х₂ Х₁Х₂ Х₁Х₂ Х₁Х₂

Простые импликанты: Х₁, Х₂

Конституенты единицы: Х₁Х₂, Х₁Х₂, Х₁Х₂

Теперь можем провести операции поглощения:

Х₁ поглощает: Х₁, Х₁Х₂, Х₁Х₂

Х₂ поглощает: Х₂ , Х₁Х₂, Х₁ Х₂

Т.е. сокращенная ДНФ

f(Х₁, Х₂)= Х₁ Х₂ в данном случае она – минимальная форма.

Пример 2:

Пусть задана:

f(Х₁, Х₂, Х₃)= Х₁Х₃ Х₁Х₂ Х₁Х₂ Х₃

f(Х₁, Х₂, Х₃)= Х₁Х₃ Х₁Х₂ Х₁Х₂ Х₃

Получим СДНФ:

f= Х₁Х₃ (Х₂ Х₂) Х₁Х₂ (Х₃ Х₃) Х₁Х₂ Х₃ = Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ = Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃

Теперь, имея СДНФ, можно получить сокращенную ДНФ:

f(X₁,X₂,X₃)=X₁X₂X₃ X₂X₃ X₁X₃

Пример 3:

f(Х₁, Х₂, Х₃)=Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ Х₁Х₂ Х₃ = Х₁Х₃ Х₂Х₃ Х₁Х₂ Х₁Х₃

Склеиваются два произведения, содержащие число переменных с отрицанием, отличающихся на единицу и расположенных соответствующим образом.

Обычно произведение, содержащее 'n' букв, называется минтермом 'n'-ранга.