Реализация КС в базисе Жегалкина
Как было рассмотрено ранее, базис Жегалкина соответствует сигнатуре 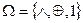 .
.
Если булева функция задана в СДНФ, переход к базису Жегалкина достаточно прост. В выражении СДНФ знак «Ú» (или) можно заменить на « 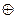 » (исключающее или). Данная замена вполне правомочна, поскольку в СДНФ при определенном наборе аргументов только один терм может давать истинное выражение.
» (исключающее или). Данная замена вполне правомочна, поскольку в СДНФ при определенном наборе аргументов только один терм может давать истинное выражение.
Пример 5.32. Представить в базисе Жегалкина и построить КС для булевой функции, заданный СДНФ:
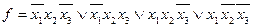 , отсюда
, отсюда
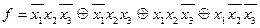 .
.
Используя, что 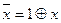 , выполним замены:
, выполним замены:
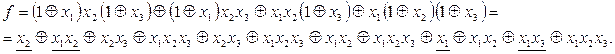
Учитывая, что 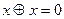 , получим
, получим
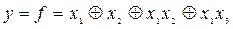 .
.
Выражение упрощается посредством вычеркивания одинаковых термов, если они повторяются в выражении четное число раз. Реализация КС показана на рис 5.27.
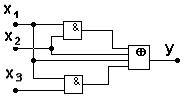
Рис. 5.27. Схема в базисе Жегалкина
Имея выражения для булевой функции в произвольной ДНФ (конечно лучше иметь минимальную форму), для перехода к базису Жегалкина можно использовать соотношение
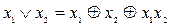 . (5.29)
. (5.29)
Пример 5.33. Для предыдущего примера 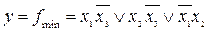 ,
,
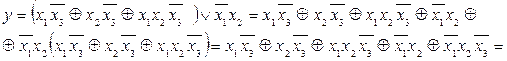
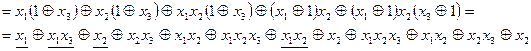
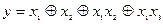 .
.
Реализация в виде КС приведена на рис. 5.27.
Синтез составных КС
В общем случае для минимизации систем ПФ может быть использован модифицированный алгоритм Квайна-Мак-Класки, рассмотренный в п. 5.2.7. Реализация КС для примера 5.27. приведена на рис. 5.28.
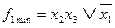 ;
;
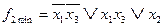 ;
;
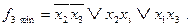
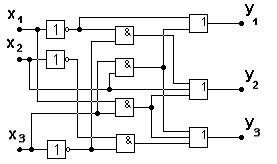
Рис. 5.28. Комбинационная схема для системы ПФ
В ряде специальных случаев при реализации систем ПФ можно ограничиться более простыми методами. Для системы из двух булевых функций рассмотрим следующие частные случаи:
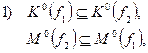
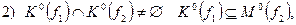
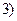 остальные,
остальные,
где 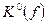 - множество 0-кубов функции f, т.е. наборов, соответствующих истинным значениям;
- множество 0-кубов функции f, т.е. наборов, соответствующих истинным значениям; 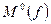 - множество наборов, соответствующих ложным значениям функции f.
- множество наборов, соответствующих ложным значениям функции f.
Рассмотрим приемы синтеза КС на примерах.
Пример 5.34. Две ПФ заданы на картах Карно (рис. 5.29).
|
|
|
|


 |  |
 | ||||||||||
 1 1 |  |
 |
 | |||||||||
 |  |  1 1 |  1 1 | |||||||||
| 1 |
|  1 1 |
|
 | |||
 |
Рис. 5.29. Представление на картах Карно системы
из двух ПФ при 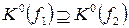
Найдем минимальные ДНФ для 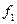 и
и 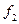 :
:
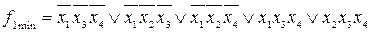 ,
,
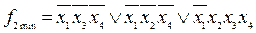 ,
,
отсюда очевидно, что здесь 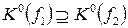 .
.
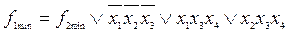 .
.
Здесь терм 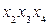 поглощает
поглощает 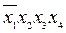 , однако последний необходимо оставить, чтобы обеспечить реализацию функции
, однако последний необходимо оставить, чтобы обеспечить реализацию функции 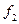 . На рис. 5.30 приводится реализация КС, реализация первого уровня, обеспечивающего инверсии входных переменных, не показана.
. На рис. 5.30 приводится реализация КС, реализация первого уровня, обеспечивающего инверсии входных переменных, не показана.

|
|
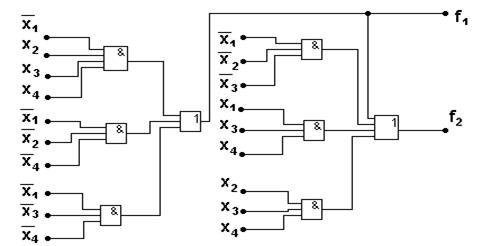
Рис. 5.30. Пример КС системы для случая 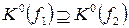
В случае 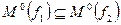 можно провести минимизацию по нулям и поступить аналогично.
можно провести минимизацию по нулям и поступить аналогично.
Пример 5.35. ПФ заданы на картах Карно рис. 5.31. Реализовать комбинационную схему.
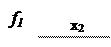 | |||
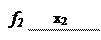 |
 |  1 1 |
  |  0 0 |  1 1 | ||||||||
  |
 |  1 1 |
 1 1 | |||||||||
  1 1 |   0 0 |  1 1 | ||||||||||
|
|
 | |||
 |
Рис. 5.31. Карты Карно для случая 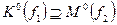
В данном случае 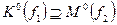 . По картам Карно получим
. По картам Карно получим
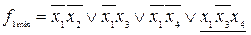 ,
,
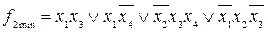 .
.
Минимизируя 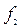 по нулям, получим
по нулям, получим
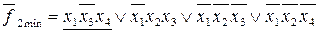 ,
,
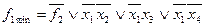 .
.
При минимизации 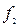 по единицам оценим сложность КС по критерию Квайна
по единицам оценим сложность КС по критерию Квайна 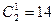 , при минимизации по нулям получим
, при минимизации по нулям получим 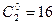 (показатели сложности получены без учета инверсий для входных аргументов, поскольку таковые уже используются для реализации
(показатели сложности получены без учета инверсий для входных аргументов, поскольку таковые уже используются для реализации 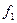 ). Таким образом, для реализации
). Таким образом, для реализации 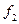 используем минимальную форму, полученную по единицам. Схема приводится на рис 5.32.
используем минимальную форму, полученную по единицам. Схема приводится на рис 5.32.
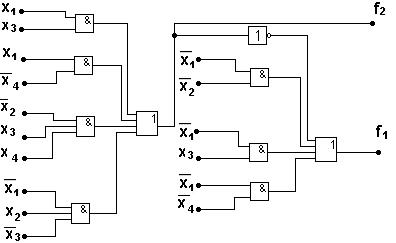
Рис. 5.32. Пример КС системы для случая 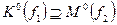
В самом общем случае мы имеем частичное перекрытие комплекса 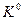 или
или 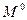 одной функции с комплексом (
одной функции с комплексом ( 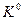 или
или 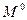 ) другой функции. В данной ситуации необходимо рассмотреть несколько вариантов реализации и выбрать наиболее эффективный, например, в смысле критерия Квайна. Здесь часто оказывается важным выделить максимально большую общую часть.
) другой функции. В данной ситуации необходимо рассмотреть несколько вариантов реализации и выбрать наиболее эффективный, например, в смысле критерия Квайна. Здесь часто оказывается важным выделить максимально большую общую часть.
Пример. 5.36.Пусть две ПФ заданы на картах Карно рис. 5.33.
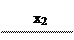 | |||||||
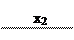 | |||||||
 | |||||||
| |||||||
 1 1 |  0 0 |  1 1 | ||||||
 1 1 |
|
|


Рис. 5.33. Пример частичного перекрытия комплексов функций
Запишем выражения для минимальных форм, используя минимизацию по единицам и по нулям:
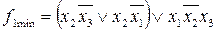 ,
,
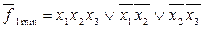 ,
,
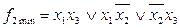 ,
,
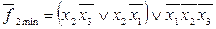 .
.
Используя выражения для 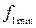 и
и 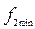 , реализуя общую часть выражения (взятую в скобки) отдельной схемой, построим КС (рис. 5.34а).
, реализуя общую часть выражения (взятую в скобки) отдельной схемой, построим КС (рис. 5.34а).
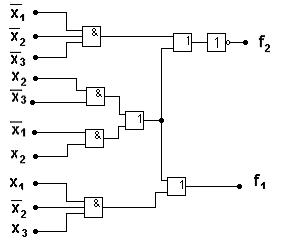
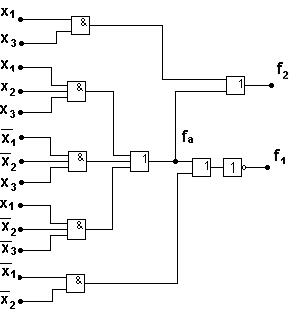
а) б)
Рис. 5.34. Примеры составных КС
Данная схема имеет сложность 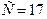 .
.
По карте Карно для 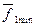 и
и 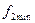 можно выделить общую часть (на рис. 5.33 отмечена пунктиром).
можно выделить общую часть (на рис. 5.33 отмечена пунктиром).
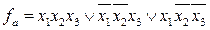 , отсюда
, отсюда
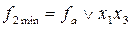 ,
,
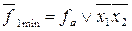 .
.
КС, реализующий данный способ, приводится на рис. 5.34б, сложность данной схемы составляет 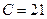 . Очевидно, что первый способ реализации более эффективный.
. Очевидно, что первый способ реализации более эффективный.
В данном учебном пособии мы рассмотрели некоторые методы и практические рекомендации к реализации комбинационных схем на ЛЭ. Более подробно с данным вопросом можно ознакомиться, например, в [9].
Вопросы для самоконтроля
1. Постройте комбинационные схемы в различных базисах для заданий к п. 5.2.
Заключение
Рассмотренные в настоящем учебном пособии фундаментальные вопросы компьютерной арифметики и логики при глубоком их изучении студентами на первом и втором курсах составляют фундамент их общепрофессиональной подготовки и в значительной степени влияют на качество подготовки специалистов.
Учебное пособие построено так, что каждый теоретический материал, читаемый на лекциях, подкреплен многочисленными примерами, используемыми при проведении практических занятий, лабораторных работ и выполнении курсового проектирования. При этом лабораторная база для закрепления на практике теоретических знаний включает более пятидесяти персональных ЭВМ на платформе Pentium 4 и выше.
Учебное пособие составлено так, что позволяет проводить аттестацию студентов по отдельным разделам дисциплин по мере их изучения и тем самым повысить качество аттестации студентов.
Изучаемые первоначально фундаментальные понятия информатики, системы счисления, алгоритмы перевода чисел из любой системы счисления в любую другую, рассматриваемые алгоритмы выполнения основных арифметических операций над числами в двоичной и десятичной системе с фиксированной и плавающей запятой, а также многочисленные алгоритмы ускоренного выполнения операций компьютерной арифметики используются далее в курсе «Алгоритмические языки и программирование» алгоритмов и программ. В этом курсе на практических занятиях студентам предлагается путем восходящего проектирования разработать универсальный алгоритм перевода чисел из любой позиционной системы счисления в любую другую, проанализировать применение в ЭВМ систем счисления с основаниями 2, 8, 10, 16 и исследовать соответствующие компьютерные арифметические операции. Методом нисходящего проектирования студенты разрабатывают универсальный алгоритм-модель функционирования операционного устройства под числами с плавающей запятой. При этом проектируется первоначально общая модель, а затем выполняется ряд этапов детализации с учетом изученных алгоритмов. На таких занятиях развивается у студентов опыт программирования относительно сложных задач в профессионально ориентированной предметной области. Проверкой качественного усвоения полученных знаний и умения применять их на практике являются выполнение студентами курсовой работы, включающей самостоятельную разработку алгоритмов и программ их реализации на языке высокого уровня.
Следующей ступенью изучения материала учебного пособия являются проработка более сложных алгоритмов двоично-десятичной арифметики, основных понятий математической логики и переключательных (булевых) функций, вопросы их минимизации, а также изучение начальных стадий логического проектирования комбинационных схем и простейших операционных устройств. Закрепление у студентов полученных на данном этапе теоретических знаний осуществляется на практических и лабораторных занятиях с использованием моделирующих программ и персональных ЭВМ.