Оценка закономерностей многолетних колебаний уровня грунтовых вод. Периодограмный анализ наиболее длинных рядов наблюдений
Задача оценки изменчивости качественных и количественных характеристик подземных вод и режимообразующих факторов важна при анализе данных мониторинга, выявлении закономерностей и прогнозирования изменения режима и качества подземных вод.
Необходимо определить следующие основные статистические xapактеристики изменчивости режимообразующих факторов, колебания уровня подземных вод, изменения их запасов и качественных характеристик: дисперсию D, стандарт и коэффициент вариация V по формулам:
 или (1)
или (1)
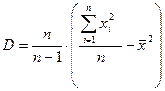 , (2)
, (2)
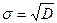 , (3)
, (3)
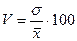 , % (4)
, % (4)
Наиболее часто встречающаяся ошибка у студентов: при расчете дисперсии по формуле (1) необходимо суммировать возведенные в квадрат разности 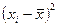 , а не суммировать
, а не суммировать 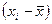 , а потом возводить сумму в квадрат.
, а потом возводить сумму в квадрат.
В формулах (1) - (4)  - значение качественного свойства в каждой точке измерения (в пробе, скважине),
- значение качественного свойства в каждой точке измерения (в пробе, скважине), 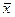 - среднеарифметическое значение свойства, определяемое по формуле:
- среднеарифметическое значение свойства, определяемое по формуле:
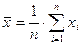 .
.
О возможных законах распределения значений  судят по вычис-ленным значениям
судят по вычис-ленным значениям 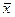 ,
, 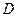 , а также по асимметрии
, а также по асимметрии 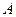 и эксцессу
и эксцессу 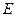 :
:
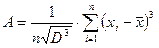 . (5)
. (5)
При 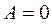 кривая плотности распределения симметричная, распределение нормальное; при
кривая плотности распределения симметричная, распределение нормальное; при 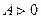 - положительная асимметрия, "хвост" кривой вытянут вправо (логнормальное, гамма- или распределение Вейбулла); при
- положительная асимметрия, "хвост" кривой вытянут вправо (логнормальное, гамма- или распределение Вейбулла); при 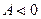 - отрицательная асимметрия, "хвост" кривой вытянут влево. Эксцесс
- отрицательная асимметрия, "хвост" кривой вытянут влево. Эксцесс 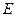 - показатель остроты пика кривой функции плотности распределения:
- показатель остроты пика кривой функции плотности распределения:
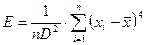 . (6)
. (6)
При нормальном законе распределения 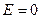 .
.
В общем случае характер изменчивости показателей месторождения определяет вид функции плотности вероятности распределения 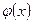 показателей
показателей 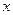 (закон распределения). Например, нормальный:
(закон распределения). Например, нормальный:
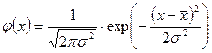 . (7)
. (7)
Предпочтительней использовать закон Вейбулла, которым можно аппроксимировать как симметричные, так и асимметричные (положительные и отрицательные распределения):
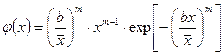 , (8)
, (8)
где: 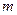 ,
, 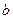 - параметры распределения, зависящие от
- параметры распределения, зависящие от 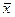 и
и 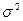 , т.е. от коэффициента вариации.
, т.е. от коэффициента вариации.
Коэффициент анизотропии изменчивости показателя в различных направлениях более точно следует определять (при достаточной длине реализаций показателя) по радиусам автокорреляции, измеряемым на графиках автокорреляционных функций, построенных в двух ортогональных направлениях. Значения корреляционной функции по каждой реализации (профилю) вычисляются по формуле:
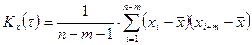 , (9)
, (9)
а автокорреляционной - по формуле:
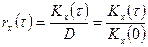 , (10)
, (10)
где: 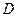 - дисперсия показателя или значение
- дисперсия показателя или значение 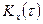 при
при 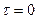 ;
; 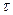 - расстояние между соседними значениями параметра
- расстояние между соседними значениями параметра 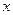 , для которого определяется значение
, для которого определяется значение 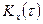 ;
; 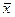 - среднее значение (математическое ожидание) параметра
- среднее значение (математическое ожидание) параметра 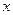 по профилю;
по профилю;
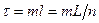 , (11)
, (11)
где: 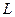 - длина npoфиля, м;
- длина npoфиля, м; 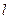 - длина шага опробования или среднее расстояние между пробами (скважинами), м;
- длина шага опробования или среднее расстояние между пробами (скважинами), м; 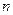 - количество скважин (точек опробования) на профиле;
- количество скважин (точек опробования) на профиле; 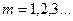 - шаг корреляционной функции (m n).
- шаг корреляционной функции (m n).
Определив значения  для различных
для различных 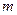 (
( 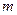 увеличивают до тех пор, пока значение
увеличивают до тех пор, пока значение  станет отрицательным) по каждому из профилей в направлении l, вычисляют его средние значения в данном направлении и строят график. Точно также определяют значения
станет отрицательным) по каждому из профилей в направлении l, вычисляют его средние значения в данном направлении и строят график. Точно также определяют значения  , его средние значения и строят график в ортогональном направлении l+90. По точкам пересечения графиков
, его средние значения и строят график в ортогональном направлении l+90. По точкам пересечения графиков  с осью абсцисс (расстояний) определяют длину радиусов автокорреляции R1 и R2 в двух ортогональных направлениях. Коэффициент анизотропии вычисляют по формуле:
с осью абсцисс (расстояний) определяют длину радиусов автокорреляции R1 и R2 в двух ортогональных направлениях. Коэффициент анизотропии вычисляют по формуле:
 ;
;  . (12)
. (12)
Радиусы автокорреляции служат также для определения оптимального окна сглаживания полигональных кривых изменения показателя по профилю или во времени при выявлении закономерной составляющей изменчивости (тренда). Оптимальное окно берется равным или чуть меньше радиуса автокорреляции (но не больше).
Зная коэффициент автокорреляции  при заданной сети выработок (заданном
при заданной сети выработок (заданном 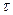 ) и общую дисперсию
) и общую дисперсию 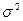 изменчивости показателя, можно вычислить доли дисперсии случайной (
изменчивости показателя, можно вычислить доли дисперсии случайной ( 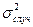 ) и закономерной (
) и закономерной ( 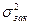 ) составляющих изменчивости по формулам:
) составляющих изменчивости по формулам:
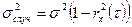 , (13)
, (13)
 . (14)
. (14)
При геометрическом анализе изменчивости метеорологических факторов можно определить коэффициенты изменчивости для полигональной или плавной кривой, построенной по рядам наблюдений:
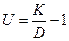 , (15)
, (15)
где 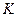 - длина кривой, измеренная курвиметром или иным способом, мм;
- длина кривой, измеренная курвиметром или иным способом, мм;
 , (16)
, (16)
где: 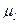 - масштабный коэффициент по оси интервалов:
- масштабный коэффициент по оси интервалов: 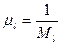 (1мм соответствует
(1мм соответствует 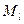 в м);
в м); 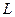 - длина проекции кривой на ось интервалов, м;
- длина проекции кривой на ось интервалов, м;
R - размах реализации (разность max и min значений показателя на данном профиле), ед.; 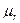 - масштабный коэффициент по оси значений показателя:
- масштабный коэффициент по оси значений показателя:
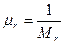 (1 мм соответствует
(1 мм соответствует 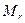 единицам показателя). Для возможности сравнения коэффициентов изменчивости, определенных по графикам с различными масштабами, вычисленные значения необходимо привести к одинаковым масштабам по осям, т.е. определить
единицам показателя). Для возможности сравнения коэффициентов изменчивости, определенных по графикам с различными масштабами, вычисленные значения необходимо привести к одинаковым масштабам по осям, т.е. определить 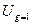 при
при 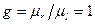 :
:
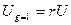 , (77)
, (77)
где 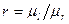 поправочный коэффициент.
поправочный коэффициент.
Осн.: 3[1-6]
Доп.: 6[1-15]
Контрольные вопросы:
1. Какие факторы определяют региональные закономерности естественного режима подземных вод?
2. Какие закономерности режима подземных вод характерны для районов развития сезонно-промерзающих пород?
3. Какие закономерности режима подземных вод наблюдаются в районах развития кратковременно промерзающих пород?
4. Какие закономерности характерны для времени наступления минимального стояния уровня грунтовых вод?
5. Закономерности температурного режима и химического состава грунтовых вод.
6. Какие статистические характеристики можно использовать для оценки изменчивости режимообразующих факторов, колебания уровня подземных вод, изменения их запасов и качественных характеристик?
