Позиционные системы счисления

Перевод чисел является важным процессом функционирования вычислительных машин, так как с помощью его осуществляются арифметические действия, адресация файлов и т.п. операции.

В вычислительных машинах применяются позиционные системы счисления. В позиционной системе счисления каждое число представляется последовательностью цифр, причем позиции каждой цифры x_i присвоен определенный вес b_i, где b – основание системы. Представление целого числа в виде степенного ряда описывается формулой:

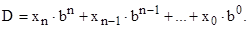
Любое число в позиционной системе счисления представляется в виде разрядов. Крайняя слева цифра называется цифрой старшего разряда, крайняя справа – цифрой младшего разряда.

Смешанное число в позиционной системе счисления представляется степенным рядом:

,

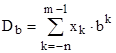где x_k–любое число из алфавита системы (набор символов) с основанием b; m и n–число разрядов соответственно для целой и дробной части числа.

В современных компьютерах используются позиционные системы счисления с основаниями 2, 8, 10 и 16, которые соответственно называются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления. Представление чисел в этих системах показано в табл.1.

Таблица 1.

Десятичные числа D10	Двоичные числа D2	Восьмеричные числа D8	Шестнадцатеричные числа D16
			А
			B
			C
			D
			E
			F

Для представления чисел в различных системах счисления необходимо вычислять степени двойки, восьмерки и шестнадцати (табл.2).

Таблица 2.

Степени двойки	Степени восьмерки	Степени шестнадцати
20=1	80=1	160=1
21=2	81=8	161=16
22=4	82=64	162=256
23=8	83=512	163=4096
24=16	84=4096	164=65536
25=32	85=32768
26=64
27=128
28=256
29=512
210=1024

Задача.

Представить число 1997 в позиционной системе счисления с основанием 10 (десятичной системе)

1997 = 1х10³ + 9×10² +9×10¹ +7×10⁰.

Представить число 1997 в позиционной системе счисления с основанием 2 (двоичной системе)

1997 = 1×2¹⁰ +1×2⁹ +1×2⁸ +1×2⁷ +1×2⁶ +0×2⁵ +0×2⁴ +1×2³ +1×2² +0×2¹ +1×2⁰ = 11111001101.

Представить число 1997 в позиционной системе счисления с основанием 8 (восьмеричной системе)

1997 = 3×8³ +7×8² +1×8¹ +5×8⁰ = 3715.

Представить число 1997 в позиционной системе счисления с основанием 16 (шестнадцатеричной системе)

1997 = 7×16² +12×16¹ +13×16⁰ = 7CD.

Задача.

Представить в двоичной форме числа 48, 57 ,511, 121. Разложим числа по степенному ряду двойки:

Решение:

48 = 32+16=1х2⁵ + 1х2⁴ + 0х2³ + 0х2² + 0х2¹ + 0х2⁰=110000₂

57 = 32+ 16+8+1 =1х2⁵ + 1х2⁴+ 1х2³ + 0х2² + 0х2¹ + 1х2⁰ = 111001₂

511=256+128+32+16+8+4+2+1 = 1х2⁸+1х2⁷ +1х2⁶+1х2⁵+1х2⁴ +1х2³+ +1х2² +1х2¹ +1х2⁰ = 111111111₂

121 = 64+32+16+8+4+2+1 = 1х2⁶+1х2 +1х2⁴+ 1х2³ + 0х2² + 0х2¹ + 1х2⁰ = =111101₂

Задача.

Представить в восьмеричной форме числа 48, 57 ,511, 121. Разложим числа по степенному ряду восьмерки:

48 = 6х8¹ + 0х2⁰ = 60₈

57 = 56 + 1 = 7х8¹ + 1х2⁰ = 71₈

511 = 448 + 56 + 7 = 7х8¹ + 7х8¹ + 7х8⁰ = 777₈

121 = 64 + 56 + 1 = 1х8¹ + 7х8¹ + 1х8⁰ = 171₈

Задача.

Представить в шестнадцатеричной форме числа 48, 57 ,511, 121. Разложим числа по степенному ряду шестнадцати:

48 = 3х16¹ + 0х16⁰ = 30₁₆

57 = 48 + 9 = 3х16¹ + 9х16⁰ = 39 ₁₆

511 = 256 + 240 + 15 = 1х16² + 15х16¹ + 15х16⁰ = 1FF ₁₆

121 = 112 + 9 = 7х16¹ + 9х16⁰ = 19 ₁₆