Выполнение арифметических операций с десятичными числами
Сложение десятичных чисел в ЭВМ
При выполнении арифметических операций над десятичными числами последние обычно представляются как целые числа, то есть числа с фиксированной справа запятой. При выполнении арифметических операций над этими числами первоначально анализируются их знаки. Если при выполнении операции суммирования окажется, что знаки десятичных слагаемых одинаковые, то такие числа складываются в прямом коде. Если же знаки слагаемых разные, то в этом случае из большего числа вычитается меньшее, то есть отрицательное число, которое в этом случае представляется в виде дополнения до 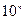 , где
, где 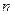 - количество десятичных разрядов в наиболее «длинном» из участвующих в операции операнде. При этом вычитание заменяется сложением положительного числа с дополнением отрицательного.
- количество десятичных разрядов в наиболее «длинном» из участвующих в операции операнде. При этом вычитание заменяется сложением положительного числа с дополнением отрицательного.
Если выполняется операция вычитания, то знак вычитаемого предварительно изменяется на обратный, после чего действия над десятичными операндами производятся так же, как и при алгебраическом сложении.
Следует помнить, что дополнение числа в двоично-десятичном коде осуществляется путем инвертирования значений двоичных разрядов в тетрадах с прибавлением единицы в младший двоичный разряд младшей тетрады по правилам двоичной арифметики. Такое дополнение получается с потетрадным избытком шесть. Поэтому, если при сложении нет переносов из каких-либо тетрад, то после выполнения сложения они должны корректироваться путем вычитания из каждой тетрады числа 6, то есть прибавления кода 1010, являющегося дополнением 6 до 16. Наличие переноса из старшей тетрады при сложении операндов с различными знаками свидетельствует о том, что результат получился в прямом коде, а отсутствие переноса свидетельствует о том, что результат получился в дополнительном коде.
Пример.
Сложить два десятичных числа 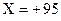 и
и 
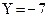 .
.
Естественные двоично-десятичные коды чисел  и
и  соответственно будут иметь вид
соответственно будут иметь вид 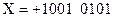 и
и 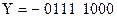 .
.
Образуем дополнение числа – 78 до 102 с избытком 6 в каждой тетраде путем инверсии разрядов кода 0111 1000 и прибавлением 1 в младший разряд младшей тетрады, тогда
1000 1000 = [Y]доп.(с избытком 6).
Теперь, опуская для простоты знаковые разряды, произведем сложение кода X с кодом [Y]доп., помня, при этом, что для положительных чисел прямой и дополнительный коды совпадают
1001 0101 X
+ 1000 1000 [Y]доп. (с избытком 6)
 ← 0001 1101 [X+Y]пр. (сумма в прямом коде
← 0001 1101 [X+Y]пр. (сумма в прямом коде
с избытком в первой тетраде)
+ 0000 1010 коррекция
 0001 0111 Х + Y = 17 (истинное значение суммы).
0001 0111 Х + Y = 17 (истинное значение суммы).
Пример.
Найти разность десятичных чисел 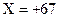 и
и 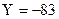 , т.е. выполнить
, т.е. выполнить 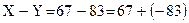 .
.
В естественной двоично-десятичной форме записи 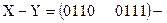
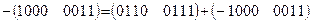 .
.
[Y] доп. (с избытком 6) равно 0111 1101, тогда операция вычитания реализуется следующим образом:
0110 0111 X
+ 0111 1101 [Y]доп. (с избытком 6)

 1110 1101 [X+Y]доп. (с избытком 6)
1110 1101 [X+Y]доп. (с избытком 6)
Перенос из стареющей тетрады отсутствует,
+ следовательно сумма отрицательная.
1010 0000 коррекция
 1000 0100 [X-Y] доп. (без избытка 6 в тетрадах).
1000 0100 [X-Y] доп. (без избытка 6 в тетрадах).
Перевод суммы в прямой код.
0111 1100 [X-Y] пр. (с избытком 6 в каждой тетраде)
 + 1010 1010 коррекция
+ 1010 1010 коррекция
0001 0110 X – Y= – 16 (истинное значение суммы).
В данном примере отсутствие переноса из старшей тетрады при сложении 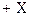 и дополнения для
и дополнения для 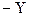 указывает на то, что результат получился отрицательный в виде дополнения. Для определения истинного значения результата следует от полученного дополнения для
указывает на то, что результат получился отрицательный в виде дополнения. Для определения истинного значения результата следует от полученного дополнения для 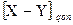 взять новое дополнение, т.е. получить прямой код
взять новое дополнение, т.е. получить прямой код 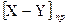 с избытком шесть, и из него потетрадно вычесть избыток 6, т.е. потетрадно прибавить 1010.
с избытком шесть, и из него потетрадно вычесть избыток 6, т.е. потетрадно прибавить 1010.
Из приведенных примеров следует, что при сложении десятичных чисел с разными знаками знак суммы определяется по наличию или отсутствию переноса из старшей тетрады. Если перенос имеет место, то результат положительный в прямом коде. Если перенос отсутствует, то получается отрицательный результат в виде дополнения. В том случае, когда при сложении чисел с одинаковыми знаками возникает перенос из старшей тетрады, то это означает наличие десятичного переноса.
Умножение и деление десятичных чисел в ЭВМ реализуется сложнее, чем соответствующие операции с двоичными числами. Рассмотрим эти операции ниже.
