Способы представления знаний- логические модели
Логические модели.
Мышление связано с решением какой-либо проблемы. Формализация мысли сводится к построению математической формы – например,логической, с использованием четко-выделенных объектов мышления. Решение проблемы связано с необходимостью делать логический вывод. Решение проблемы – это цепочка логических построений . Дж. Пирс в качестве методов логического вывода называет метод дедукции, индукции, метод построения гипотез.
Логические модели строятся на основе логики высказываний и исчисления предикатов []. Логика высказываний используется для решения логических задач алгебраическим методом. Каждое утвердительное предложение называется высказыванием. Высказывание рассматривается как истинное или ложное. Над высказыванием можно выполнять логические операции. Примеры высказываний; “Сигналы поступают на шину адреса”, ”Студенты сдают экзамен”. Из простых высказываний строятся составные, используя логические связки (и, или, не). Выражения, которые представляются простыми и сложными высказываниями образуют формулу. Идея решения задач с использованием логики высказывания состоит в том, чтобы сначала описать ситуацию, используя формулы логики высказывания, а затем доказать общезначимость или противоречивость всей совокупности этих формул. Общезначимая формула истинна при всех интерпретациях, а противоречивая – ложна при всех толкованиях.
Пример.
| Простые высказывания | Иванов студент. Студент сдает экзамен. | (А) (В) |
| Сложное высказывание | Если Иванов студент То Иванов сдает экзамен | (А®В) |
Чтобы удовлетворительно описать предметную область, для обозначения различных объектов вводятся переменные.
Для создания логических моделей можно использовать формулы логики предикатов 1-го порядка [].
Предикат – это логическая функция, которая состоит их предикатного символа и упорядоченного множества аргументов. Предикатный символ используется для представления отношений между объектами.
В отличие от логики высказываний число интерпретаций этой формулы велико.
Задача записывается как набор высказываний, отношений между высказываниями и правил вывода одних высказываний из других. Далее проверяется истинность исходных высказываний.
Для представления информации можно использовать конструкции языка Пролог.
Например:
| Правило на языке высказываний: 1 .Иванов - студент. 2. Студенты сдают экзамены. 3. Вывод: Иванов сдает экзамен. | Правило на языке Пролог: сдает_экзамен (X):– student (X). student (“Иванов”). |
Способы представления знаний - семантические сети.
Семантические сети.
При разработке ЭС для графического представления знаний могут использоваться семантические сети. Семантический подход – попытка воспроизвести графически сложные ассоциации, которые возникают у человека при обмене мыслями, это метод организации сложных массивов знаний. Сеть состоит из узлов, изображаемых окружностями, и соединяющих их линиями со стрелками. В узлах располагаются объекты, понятия и события, а связи между узлами указывают на природу взаимозависимостей. Итак, семантическая сеть - это соединение узлов знаний. При логическом выводе, который использует такую сеть, свойства, которыми обладает объект, указанный в вышестоящих узлах через связи наследует свойства заключенные в нижестоящих узлах. Семантическую сеть можно использовать для задания структур и объектов, а также для создания правил БЗ. Семантическая сеть представляющая фрагмент базы знаний приведена на рис. 3.2.
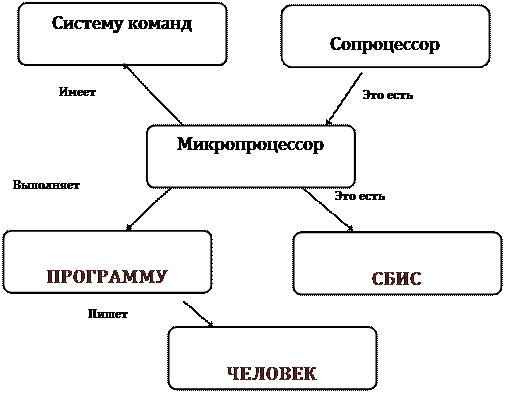 |
рис.3.2. Семантическая сеть, отражающая взаимоотношения между атрибутами микропроцессора и программы.
Можно создать объект, для этого разрабатываем структуру, описывающую все объекты с общим названием МИКРОПРОЦЕССОР.
СОЗДАТЬ_СТРУКТУРУ (имя = микропроцессор,
атрибут = CБИС,
атрибут = система команд,
атрибут = выполнять программу)
На основе этой структуры можно создать объект и ряд правил
ЕСЛИ
атрибут=СБИС &
атрибут=система команд &
атрибут=выполнять программу,
ТО объект= микропроцессор
Чем чаще используется слово, тем более оно семантически значимо.
