Моменты случайных погрешностей
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами [3].
Начальным моментом n-го порядка результатов наблюдений называется интеграл вида
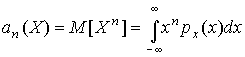 | (14) |
представляющий собой математическое ожидание степени 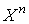 .
.
При n=1
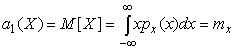 | (15) |
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n-го порядка результатов наблюдений называется интеграл вида
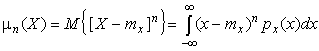 | (16) |
Вычислим первый центральный момент:
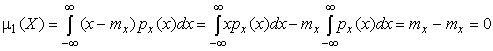 | (17) |
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.
При n=2
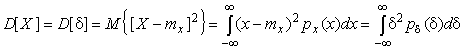 . . | (18) |
Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.
Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести.
Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений:
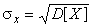 . . | (19) |
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины 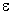 , т. е. вероятность
, т. е. вероятность 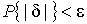 . Для этого рассмотрим формулу, известную как неравенство Чебышева:
. Для этого рассмотрим формулу, известную как неравенство Чебышева:
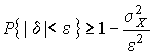 или или 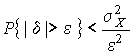 . . | (20) |
Полагая 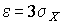 , можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше
, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше 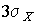 :
:
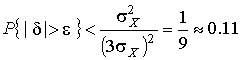
Вероятность того, что погрешность измерения не превысит 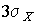 , составит соответственно
, составит соответственно
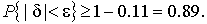
Неравенство Чебышева дает только нижнюю границу для вероятности 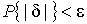 , меньше которой она не может быть ни при каком распределении. Обычно
, меньше которой она не может быть ни при каком распределении. Обычно 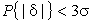 значительно больше 0.89. Так, например, в случае нормального распределения погреш-ностей эта вероятность составляет 0.9973.
значительно больше 0.89. Так, например, в случае нормального распределения погреш-ностей эта вероятность составляет 0.9973.
Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков.
Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения. Действительно, если распределение обладает свойством симметрии, то все функции вида 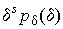 , где s = l, 3, 5..., являются нечетными функциями
, где s = l, 3, 5..., являются нечетными функциями 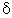 (рис.3).
(рис.3).
Поэтому все нечетные моменты, являющиеся интегралами этих функций в бесконечных пределах, должны равняться нулю. Отличие этих моментов от нуля как раз и указывает на асимметрию распределения. Простейшим из нечетных моментов является третий момент 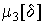 . Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии, или просто асимметрию Sk распределения:
. Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии, или просто асимметрию Sk распределения:
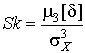 | (21) |
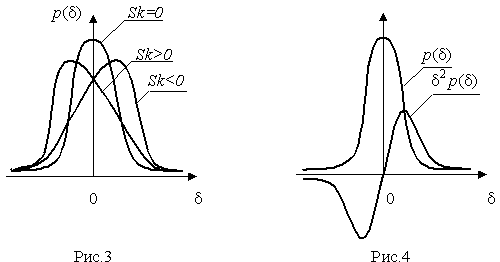
Для иллюстрации сказанного на рис.4 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией.
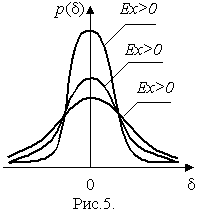
Четвертый момент служит для характеристики плосковершинности или островершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса - безразмерной характеристики, определяемой выражением
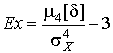 | (22) |
Число 3 вычитают из отношения 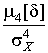 потому, что для широко распространенного нормального распределения погрешностей
потому, что для широко распространенного нормального распределения погрешностей 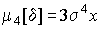 . Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные - положительным (рис.5).
. Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные - положительным (рис.5).