Постановка задачи синтеза автоматов
Задача синтеза конечных автоматов заключается в построении сложного автомата из более простых автоматов, называемых элементарными. Чаще всего применяют элементарные автоматы с двумя внутренними состояниями, которые соединяются между собой с помощью логических элементов.
Различают задачи абстрактного и структурного синтеза дискретных автоматов. Задача абстрактного синтеза заключается в получении таблиц переходов и выходов автомата (либо графа автомата).
При решении задачи структурного синтеза таблицы переходов и выходов автомата считаются заданными. Кроме того, задается или выбирается набор элементарных автоматов и логических схем. В результате синтеза следует получить структурную схему автомата.
Структурно полные системы автоматов.
Теорема о структурной полноте
Для синтеза конечных автоматов необходимо выбрать систему элементов, из которых должны строиться заданные автоматы. В большинстве схем дискретного действия в качестве элементов памяти применяются элементарные автоматы Мура с двумя внутренними состояниями (0 и 1).
Набор элементарных автоматов и логических элементов называют структурно полным, если из элементов этого набора можно построить любой дискретный автомат.
Введем понятие полноты системы переходов и выходов. Говорят, что автомат обладает полной системой переходов, если для каждой пары его внутренних состояний aiи ajнайдется хотя бы один входной сигнал, или комбинация входных сигналов для автоматов, имеющих несколько входов, который переводит автомат из состояния aiв состояние aj. Это условие должно соблюдаться как при i¹j, так и при i=j.
Говорят, что автомат Мура обладает полной системой выходов, если в каждом состоянии автомат выдает выходной сигнал, отличный от сигналов, выдаваемых в других состояниях.
Все реальные автоматы Мура имеют полную систему выходов. Если бы выходные сигналы автомата, соответствующие различным состояниям, совпадали, то состояния автомата были бы физически неразличимы.
Теорема. Для того, чтобы набор элементов был функционально полным для синтеза конечных автоматов, необходимо и достаточно, чтобы он содержал:
- хотя бы один элементарный автомат с двумя различными состояниями, для которых соблюдаются условия полноты переходов и выходов;
- логические элементы, образующие функционально полную систему для синтеза логических схем.
Элементарные автоматы
В большинстве схем современных электронных цифровых машин и других дискретных устройств автоматики в качестве элементов памяти применяются элементарные автоматы, имеющие следующие особенности.
1. Элементарные автоматы являются автоматами Мура и имеют два внутренних состояния.
2. Двум внутренним состояниям элементарного автомата соответствуют два различных выходных сигнала. Обычно обозначают в таких автоматах внутренние состояния и выходные сигналы одинаковыми буквами Q и кодируют цифрами 0 и 1.
3. Элементарные автоматы имеют в общем случае несколько физических входов, на каждый из которых могут подаваться сигналы 0 и 1.
Элементарные автоматы с одним входом. Существуют только четыре типа элементарных автоматов с одним входом, которые имеют детерминированную и полную систему переходов.

На рис. 39 представлены все возможные элементарные автоматы с одним входом, удовлетворяющие условиям детерминированности и полноты системы переходов. В этих таблицах приняты следующие обозначения: q(t)- входной сигнал в моменты времени t, Q(t) – состояние и выходной сигнал, Q(t+1) - состояние и выходной сигнал в момент времени t+1. Таблицы а-в и б-г отличаются друг от друга только способом кодирования входных сигналов q(t) и, следовательно, после перекодирования последних полностью совпадают. Таким образом, имеется лишь два принципиально различных элементарных автомата с одним входом.
Элементарный автомат, заданный таблицей а (в), представляет собой элемент задержки входных сигналов на один такт. Такой элемент получил название D-триггер.
Элементарный автомат, заданный таблицей б (г), изменяет свое состояние только при подаче на вход сигнала, равного единице. Такой автомат называется триггером со счетным входом, или Т-триггером.
Запишем функции переходов автоматов в аналитической форме. Для автомата, представленного таблицей а):
Q(t+1)=  .
.
Для Т-триггера (таблица б):
 .
.
Элементарные автоматы с двумя входами. Обозначим входы автомата через q0и q1. Автомат функционирует следующим образом: если на входе q0 действует сигнал, равный единице (нулю), а на входе q1 - равный нулю (единице), то автомат переходит в состояние нуль (единица) независимо от его состояния в предыдущий момент времени. Если на вход автомата подаются импульсные сигналы, закодированные так, что код 0 означает отсутствие импульса, то комбинация входных сигналов q0=0, q1=0 не может изменить состояние автомата. В этом случае в первой и второй строках таблицы переходов (рис. 40) код состояния Q(t+1) должен совпадать с кодом состояния Q(t). Следует также учитывать, что на практике встречаются схемы автоматов, которые под воздействием некоторых комбинаций входных сигналов работают неустойчиво (чаще всего q0=1, q1=1). Такие комбинации считают запрещенными и специальными
схемами на входе такого автомата их появление исключают. Автомат подобного типа.
получил название R-S-триггер. Вход q0 обычно обозна-
| q0 | q1 | Q(t) | Q(t+1) | чают буквой R, а вход q1 - буквой S. Для представления функции переходов автомата в аналитической форме в виде функции алгебры логики воспользуемся картой Карно (рис. 41). Проставив в пустых клетках карты единицы, получим:  Запрещение подачи на вход одновременно сигналов q0=1 и q1=1 можно записать в виде равенства q0q1=0. Запрещение подачи на вход одновременно сигналов q0=1 и q1=1 можно записать в виде равенства q0q1=0. | |
| - | |||||
| - |
Рис.40. Таблица переходов Отметим, что подобный триггер может быть пере-
R-S-триггера веден из состояния Q(t) =0 в состояние Q(t+1)= 0 двумя
различными комбинациями входных сигналов: q0=0, q1=0 и q0=1, q1=0. Переход из состояния Q(t)=1 в состояние Q(t+1)=1 также может быть вызван двумя комбинациями входных сигналов: q0=0, q1=0 и q0=0, q1=1.
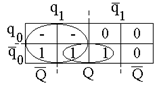 Рис. 41. Карта Карно R-S - триггера Рис. 41. Карта Карно R-S - триггера | Автоматы, которые могут переходить из одного состояния в другое или в то же самое состояние под влиянием нескольких комбинаций входных сигналов, называют автоматами с избыточной системой переходов. На рис.42 приведена таблица переходов триггера с двумя входами, у которого отсутствуют запрещенные комбинации входных сигналов. Если на вход этого триггера подать комбинацию сигналов q0=1, q1=1, | ||||||||||||||
| q0 | q1 | Q(t) | Q(t+1) | ||||||||||||
| q1 | q1 | ||||||||||||||
| q0 | |||||||||||||||
| q0 | |||||||||||||||
| Q | Q | Q | |||||||||||||
| Рис.43. Карта Карно J-K-триггера | |||||||||||||||
| Рис.42. Таблица пере - ходов J-K-триггера | то он изменит свое состояние. Такой триггер получил название J-K-триггер. Для J-K-триггера вход q0 обозначается буквой K, а вход q1 - буквой J. По логической функции переходов элементарного автомата может быть построена его логическая схема. | ||||||||||||||
. Так, для R-S-триггера логическая функция переходов имеет вид:
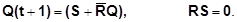
Построим схему триггера на элементах И-НЕ. Для перевода заданной функции в базис И-НЕ сделаем двойное отрицание правой части и преобразуем по правилу де Моргана:
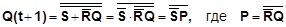
Логическая схема R-S-триггера, построенная по последнему выражению, показана на рис. 44. Элемент 1 в схеме обеспечивает условие RS=0.

Рис. 44. Логическая схема R-S-триггера на элементах И-НЕ
По способу записи информации триггерные устройства делятся на асинхронные и тактируемые. В асинхронных триггерах запись информации осуществляется непосредственно с поступлением информационных сигналов на его входы. Запись информации в тактируемых триггерах, имеющих информационные и тактовые входы, осуществляется только при подаче разрешающего, тактового импульса. На рис. 45 показана схема тактируемого R-S-триггера на элементах И-НЕ. На схеме R, S - информационные входы, C - тактовый вход.
Условные изображения некоторых триггеров показаны на рис. 46.

Рис. 45. Тактируемый R-S-триггер

Рис. 46. Условные обозначения триггеров: а - D, б - Т, в - R-S, г - J-K
