Минимизация логических выражений

Методы минимизации основываются на законах алгебры логики, позволяющих осуществлять преобразования алгебраических выражений (формул) с целью получения упрощенных минимальных форм функций.

Важным этапом синтеза сложных дискретных устройств же­лезнодорожной автоматики, телемеханики и связи является опре­деление способа соединения между собой логических элементов, обеспечивающих работу устройства телемеханики в соответствии с заданным законом функционирования. На этом этапе требуется представить функцию алгебры логики устройства через функции выбран­ной полной системы (базиса).

Важной задачей является упрощение выражений для ФАЛ с целью получения такого вида формулы, при котором построенный в соответствии с ней автомат отличался бы минимальным расходом логических элементов на его изготовление.

Любая функция алгебры логики выражается через исходные функции неоднозначно. Поэтому требуется найти такую форму ее представления, которая позволяет построить наиболее простую электрическую схему для синтеза более сложных функциональных импульсных устройств, составляющих систему телемеханики. При решении этой задачи заданную функцию алгебры логики дискретного устройства вначале оказывается удобным представить в некоторой исходной канонической форме, которую называют нормальной, а затем преобразовать ее так, чтобы она соответствовала наиболее простой электрической схеме с учетом выбранного базиса логических элементов.

Каноническими формами представления функций алгебры логики являются совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).

Совершенная дизъюнктивная нормальная форма ФАЛ представляет собой дизъюнкцию специально вводимых вспомогательных функций - конституент единицы (минтермов), которые равны 1 на тех же наборах, что и заданная функция. СДНФ представляет собой алгебраическое выражение, которое принимает значение, равное 1 на тех наборах переменных, на которых значение заданной функции равно 1. Конституентой единицы называют функцию, которая принимает значение 1 на одном из всех возможных наборов переменных. В табл.1 приведены функций f (x₁, х₂, х₃) и φ (х₁, x₂, х₃) трех аргументов. Среди них имеется конституенты единицы: наборы 1, 3, 7 для функции f (x₁, х₂, х₃) и наборы 0, 4, 6, 7 для φ (х₁, x₂, х₃). Количество конституент единицы заданного числа переменных п, как следует из опре­деления, совпадает с числом различных наборов К=2п. Для со­ставления алгебраического выражения, принимающего значение, равное 1, на всех наборах, на которых функция равна 1, следует взять дизъюнкцию конституент, соответствующих этим наборам;

Дизъюнктивной нормальной формой (ДНФ) называется такая форма представления функции, когда она выражается дизъюнкцией простых конъюнкций аргументов или их инверсий:

.

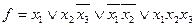Если в каждой конъюнкции ДНФ присутствуют все аргументы функции, то такая форма носит название СДНФ:

.

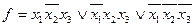Для перехода от ДНФ к СДНФ необходимо в каждой из ее членов путем умножения их на выражения вида 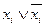ввести недостающие аргументы:

.

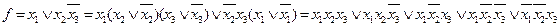СДНФ может быть получена непосредственно из таблицы истинности. При этом каждый член ее будет соответствовать набору аргументов, при котором функция равна 1.

Конъюнктивной нормальной формой (КНФ) называется форма представления функции в виде конъюнкции простых дизъюнкций аргументов или их инверсий:

.

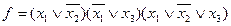Если каждый член КНФ содержит все аргументы, то такая форма будет совершенной конъюнктивной нормальной формой

.

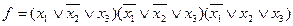Для перехода от КНФ к СКНФ необходимо к каждому члену КНФ прибавить выражение вида 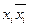где х_i - недостающий аргумент:

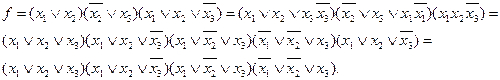
Для получения СКНФ из таблицы истинности необходимо представить в виде инверсий наборы аргументов, при которых функция принимает значения 0, и соединить их знаками конъюнкции.

По каноническим формам (СДНФ и СКНФ) могут быть непосредственно построены логические устройства, однако, как правило, в этих случаях схемы содержат большое количество элементов и прежде, чем составлять логические схемы, производят упрощение (минимизацию) функций.

Наиболее детально разработаны методы решения канони­ческой задачи минимизации ФАЛ, которая заключается в нахождении формы функции, содержащей минимальное число вхождений переменных. Такие формы называют минимальными.

Под минимизацией понимают процесс нахождения такого эквивалентного выражения логической функции, которое содержит минимальное число вхождений переменных. Хотя в общем случае под минимизацией может иметься в виду получение выражений с минимальным числом инверсных переменных либо с минимальным числом вхождений какой-либо одной переменной. Большинство методов минимизации ориентированы на получение минимальных ДНФ (минимальных КНФ), однако доказано, что минимальное выражение в классе ДНФ будет также минимальным, либо отличаться от минимального на одно вхождение переменной в классе других форм функции.

Исходными формами функции при решении канонической зада­чи минимизации являются ее СДНФ и СКНФ. Если функция задана в другой форме, последнюю преобразуют в СДНФ или СКНФ. как это было показано ранее. Рассмотрим минимизацию функций, заданных в дизъюнктивной нормальной форме.

Минимальной ДНФ (МДНФ) называют такую запись функции, которая содержит самое минимальное число переменных по сравнению со всеми другими ДНФ, эквивалентными данной функции. Существуют различные методы минимизации ФАЛ. Все они основаны на попарном склеивании соседних конституент, отличающихся значениями только одной переменной, применяя закон склеивания. В одну конституенту переменная входит в прямой форме, в другую - в инверсной. Две соседние конституенты склеиваются по различающейся переменной, что приводит к замене их одной конъюнкцией с числом переменных, на единицу меньшим, чем в исходных конституентах.

Конъюнкции, получаемые в результате склеивания двух сосед­них конституент, называют импликантами. Различные импликанты с одинаковым числом переменных в свою очередь могут оказаться соседними, что позволяет склеивать их между собой. Процесс многоступенчатого склеивании приводит к получению импликант, которые не склеиваются с другими. Такие импликанты называются простыми.

Импликанта, полученная в результате склеивания некоторого множества конституент покрывает (поглощает) эти конституенты. Так, импликанта может покрывать несколько исходных конституент, каждая из которых содержит, например, четыре переменные.

Наиболее эффективна минимизация булевых функций с помощью карт Карно. До сих пор существует ошибочное мнение, что этим методом можно решать задачи для функций от не более, чем 6 аргументов. На самом деле карты Карно могут применяться для функций даже от 8-12 переменных. Этот метод минимизации функции производится посредством таблицы, которая называется картой Карно. Карта Карно – это таблица, содержащая 2n ячеек. Количество клеток в карте Карно равно количеству строк в таблице истинности. Каждая клетка соответствует одной строке таблицы. Комбинации входных переменных распределяются по двум сторонам прямоугольника, а соответствующие значения функции в клетках таблицы, находящихся на пересечении строк и столбцов, соответствующих выбранным состояниям переменных. Каждой ячейке соответствует определенный набор переменных и указывается какое значение на этом наборе принимает функция. Причем соседние ячейки отличаются значением только одной переменной, что позволяет минимизировать ДНФ, используя закон склеивания. Метод Карно основан на законе склеивания. Склеиваются наборы, отличающиеся друг от друга лишь значением одного разряда. Такие наборы называются соседними, и они соответствуют соседним клеткам карты Карно. Формируются такие наборы (коды Грея) по принципу симметрии), объединяя ячейки по 2ⁿ в прямоугольники, которые называются контурами. Соседними являются крайние верхние и крайние слева и справа. Необходимо стремиться к тому, чтобы контуры содержали как можно больше ячеек. А количество контуров должно быть минимально возможным. При создании контуров одну и туже ячейку (конъюнкцию) можно включать в несколько контуров в соответствии закона идемпотентности (повторное действие над объектом не изменяет его). Каждому контуру соответствует конъюнкция. При соединении двух ячеек исключается одна переменная, четырех – две, восьми – три и т.д. При объединении ячеек исключаются, согласно закона склеивания, переменные, которые входят в конъюнкции с разными значениями.

Упрощение выражений булевых функций (минимизация) основывается на понятии несущественности переменных. Переменная называется несущественной на паре наборов, если при изменении ее значения на противоположное булева функция сохраняет свое значение. Например, для булевой функции трех переменных:

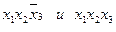
по дистрибутивному закону:

.

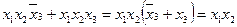Таким образом, две конъюнкции, содержащие несущественную переменную, заменяются одной, в которой несущественная переменная отсутствует.

Приведем основные определения, используемые при минимизации булевых функций. Данные определения используют понятия нормальных (канонических) форм булевых функций.

Число переменных, входящих в элементарную конъюнкцию (для ДНФ) или в элементарную дизъюнкцию (для КНФ) называется ее рангом.

В основе любых методов минимизации лежит операция склеивания. Два элементарных произведения одного ранга (для ДНФ) или элементарных сумм одного ранга (для КНФ) склеиваются, если они различаются только по одной переменной.

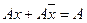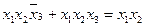Операция, показанная выражениями и называется полным склеиванием, а операция, выраженная в следующем виде:

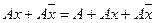и ,

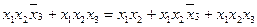называется неполным склеиванием (для ДНФ).

Импликантой - называется элементарное произведение, равное 1 на одном или нескольких наборах, где данная функция равна 1, и равное 0 на всех наборах, где данная функция равна 0. Импликанта покрывает один или несколько минтермов рассматриваемой булевой функции. Обычно, импликанта - это результат склеивания соответствующих минтермов или импликант.

Простая импликанта - это импликанта, которая содержит хотя бы минтерм функции, но перестает быть импликантой после удаления любого аргумента (иными словами, это импликанта, к которой не нельзя применить операцию склеивания).

Сокращенная ДНФ - это дизъюнкция всех простых импликант.

Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е были соседними. Поэтому значения переменных в столбцах и в строках карты образуют соседний код Грея. Такой способ представления очень удобен для наглядности при минимизации булевых функций. Карта Карно 4 переменных, с точки зрения определения "соседства" переменных, геометрически представляет собой пространственную фигуру тор или, проще говоря, "бублик".

Метод карт Карно применим к минимизации булевых функций до 6-ти переменных (до 4 переменных на плоскости) и до 6 - в трехмерной интерпретации.

Если исходная функция задана в виде какой-либо формулы, наборы, на которых функция равна 1, определяют методом перебора переменных, при этом обеспечивается развертывание формулы в СДНФ. В заполненной карте Карно наглядно отображаются соседние конституенты: им соответствуют 1, расположенные в соседних клетках. Все клетки, содержащие 1, объединяются в замкнутые области, каждая область должна представлять собой прямоугольник с числом клеток 2, 4, 8. Области могут пересекаться, и одни и те же клетки могут входить в разные области. Соседними клетками являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки, находящиеся на противоположных границах карты.

При охвате клеток замкнутыми областями следует стремиться к минимальному числу областей, каждая из которых содержала бы возможно большее число клеток. Каждый член МДНФ составляют лишь из тех переменных, которые для соответствующей области имеют одно значение: без инверсии или с инверсией. Если переменная для одной клетки области имеет значение без инверсии, а для другой клетки этой области -с инверсией, она в соответствующем члене МДНФ не присутствует.

Для получения минимальной конъюнктивной нормальной формы функции замкнутыми областями охватываются клетки с нуле­выми значениями функции и при записи членов МКНФ берутся инверсные значения переменных с неизменным значением в пределах соответствующих областей.

Правила минимизации с использованием карт Карно:

1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.

2. Количество клеток внутри контура должно быть целой степенью двойки (1, 2, 4,8, 16...).

3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).

4. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.

5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.

6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ). Целью минимизации является нахождение минимальной из множества тупиковых форм.

7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0. Для значений булевой функции, равных 0, записываются элементарные дизъюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1.

Если рассматривать запись результатов минимизации в кубическом виде, то при минимизации булевой функции по единичным значениям, каждой конъюнкции ранга R соответствует куб ранга R, где каждой переменной без инверсии соответствует 1 в кубе, переменной с инверсией - 0, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует единичное покрытие C¹ (соответствующее ДНФ). При минимизации булевой функции по нулевым значениям и представлении результатов минимизации в кубическом виде, нулевое покрытие C⁰ формируется на основе обратной ДНФ , которая является инверсной функцией по отношению к КНФ (способ построения инверсных функций и пример инверсных функций для f ( 1,3,5,6,7 ) = 1. Отметим, что обратная ДНФ строится на основе КНФ. Таким образом, каждой дизъюнкции ранга R (из КНФ) соответствует куб ранга R, где каждой переменной без инверсии соответствует 0 в кубе, переменной с инверсией - 1, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует нулевое покрытие C⁰.

В качестве примера рассмотрим минимизацию булевых функций трех переменных f (1,3,5,6,7) = 1 и четырех переменных f ( 3,7,11,12,13,14,15) = 1.

На рис. 5, а, б показано получение аналитических и кубических результатов минимизации булевой функции с использованием карт Карно.

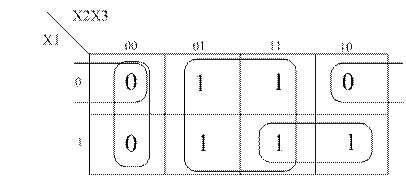
Рисунок 5, а - Карта Карно трех аргументов

Рисунок 5, б - Получение аналитических и кубических результатов

минимизации булевой функции трех переменных с использованием карт Карно

На рис. 6 показан процесс минимизации и получения аналитических и кубических выражений при минимизации булевой функции четырех переменных.

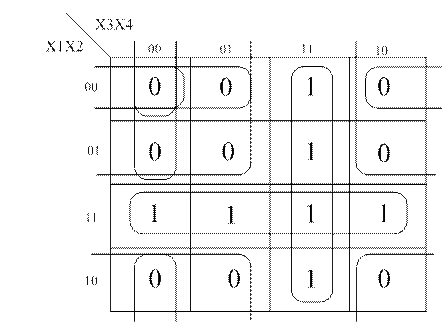
Рисунок 6 - Получение аналитических и кубических результатов

минимизации булевой функции четырех переменных

с использованием карт Карно

Исходя из способа кодировки переменных в строках и столбцах карты Карно соседним кодом Грея, с учетом сохранения "физического" соседства соседних клеток карты, на плоскости можно изобразить карту до 4-х переменных включительно. В реальной работе с булевыми функциями большего числа переменных также могут использоваться карты Карно, имеющие специальную форму.

Метод минимизации булевых функций с использованием карт Карно является одним из самых наглядных и удобных с позиций инженерной практики.

Интервалом l-го ранга называется подмножество вершин двоичного n-мерного куба, соответствующее элементарной конъюнкции l-го ранга.

Покрытием l-го ранга называется подмножество клеток карты Карно n-го порядка, соответствующее элементарной конъюнкции l-го ранга.

При задании булевой функции в виде ДНФ, будет задано и множество ее единичных значений, что будет соответствовать комбинации интервалов на пространственном кубе или комбинации покрытий на карте Карно.

Например, рассмотрим функцию трех переменных:

.

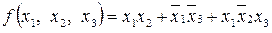ДНФ содержит три конъюнкции, которые представляются следующими интервалами (рис. 7.). На карте Карно получатся следующие покрытия (рис. 8.). Таким образом, существует взаимно однозначное соответствие между ДНФ, интервалами пространственного куба и покрытиями на карте Карно.

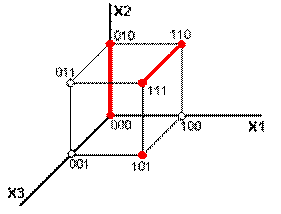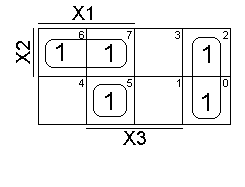Рисунок 7 - ДНФ, содержащая три конъюнкции	Рисунок 8 - Карта Карно ДНФ нестандартная

Задача нахождения МДНФ может быть сформулирована как задача построения такого множества покрытий единичных значений булевой функции, при котором сложность ДНФ будет минимальной.

Графически это означает, что необходимо и достаточно найти множество покрытий минимального ранга, представляющих множество единичных значений булевой функции.

МДНФ для рассматриваемой функции можно построить из трех интервалов второго ранга на пространственной решетке, что соответствует трем покрытиям 2-го ранга на карте Карно (рис. 9, рис. 10.).

В правильности графического способа минимизации легко убедиться, выполнив некоторые аналитические преобразования в соответствии с законами алгебры логики.

Построение МДНФ является неоднозначным процессом, так как для данной функции может существовать несколько МДНФ, и сам процесс выбора покрытий строго не формализован.

Однако, как уже отмечалось графический метод хорошо работает для логических функций первой группы и в принципе, может применяться для функций 3-й группы, что вполне приемлемо в инженерной практике.

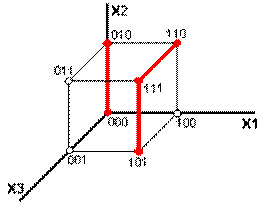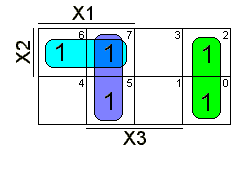Рисунок 9 - МДНФ рассматриваемой функции	Рисунок 10 - Карта Карно МДНФ карта нестандартная

Сокращенная КНФ - это конъюнкция всех простых импликант.

Тупиковая КНФ - это конъюнкция простых импликант, из которых ни одна не является лишней.

МКНФ (минимальная КНФ) - тупиковая КНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.

Исходными формами функции при решении канонической задачи минимизации являются ее совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной.

В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.

Например:

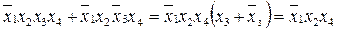
Возможность поглощения следует из очевидных равенств:

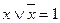и .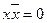

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции n переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2n различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную n–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

На рис. 11 изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

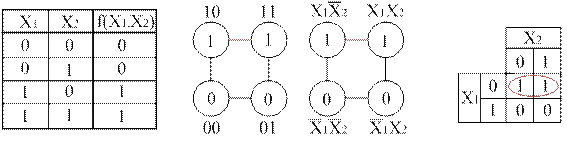
Рисунок 11 - Таблица истинности для функции двух переменных,

соответствующий этой таблице 2-мерный квадрат,

2-мерный куб с обозначением членов СДНФ

и карта Карно группировки термов

Для случая функции трёх переменных имеют дело с трёхмерным кубом (рис. 12). Это сложнее и менее наглядно, но технически возможно.

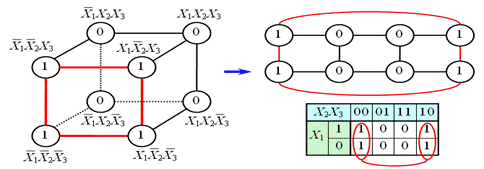
Рисунок 12 - Графический и координатный способ представления функции двух переменных

Как видно из рисунка 12, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

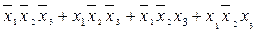
В общем случае можно сказать, что 2n термов, принадлежащие одной n –мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются n переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскости как показано на рис. 13.

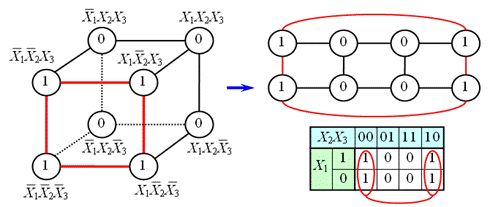
Рисунок 13 - Развертывание на плоскости

куба, представляющего собой структуру термов

Таким образом, появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для n₁ =4 и n₂ =5 приведены на рис. 14. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки.

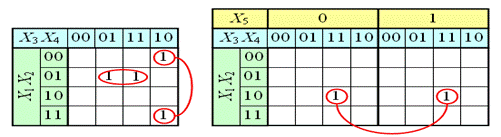
Рисунок 14 - Развертывание на плоскости функций

четырех и пяти переменных

Пример. Минимизировать функцию

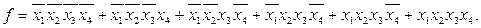
Для получения сокращенной формы проводим операции склеивания и поглощения, причем результаты склеивания вводим в выражение функции, а затем проводим операцию поглощения:

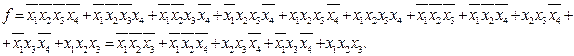
Полученное выражение представляет собой сокращенную форму заданной функции, а члены его - простые импликанты. Переход от сокращенной формы к минимальной осуществляется с помощью импликантной матрицы, представленной в виде табл. 3.

Таблица 3 - Импликантная матрица

Простые импликанты	Члены СДНФ
	×	×
	×		×
			×	×
				×	×
					×	×

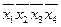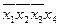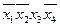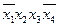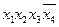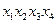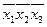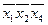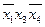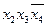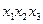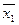
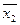
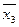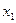
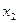
В таблице отмечаются столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. По таблице определяются импликанты, которые не могут быть исключены из сокращенной формы (составляют ядро функции). К ним относятся такие, для которых в таблице имеется хотя бы один столбец, перекрываемый только данной импликантой. В приведенном примере ядро составляют импликанты и 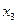. Только ими перекрываются второй и шестой столбцы матрицы. Теперь для получения минимальной формы следует выбрать минимальное количество из оставшихся импликант, чтобы перекрыть еще не перекрытые столбцы (четвертый и третий в нашем примере). В рассматриваемом случае такой импликантой будет

.

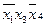Тогда минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции:

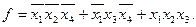
При применении метода Квайна для получения минимальной конъюнктивной нормальной формы (МКНФ) логической функции операции склеивания и поглощения имеют вид:

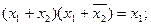
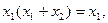
а минимизация проводится в том же порядке, что и для СДНФ.

Пример. Минимизировать СКНФ функции

.

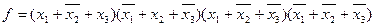Склеиваемые члены: первый и третий (результат 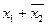); второй и четвертый (результат 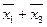); третий и четвертый (результат ).

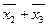После проведения операции склеивания получим:

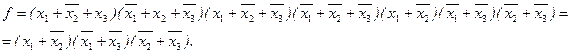
Импликантная матрица для рассматриваемой функции представляется табл. 4.

Все столбцы перекрываются двумя импликантам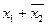и и 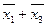. Следовательно, МКНФ функций будет

.

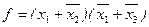Таблица 4 - Импликантная матрица

Простые импликанты	Члены СКНФ
	×		×
		×		×
			×	×
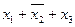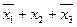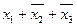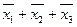
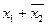
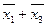
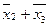