Линейно-квадратичная модель оценки риска
Линейно-квадратичная модель использует следующий вид связи между дозой токсиканта и откликом на нее:
qe = aD + bD2. (5.10)
Eсли имеются две пары значений, полученных в результате предварительных (экспериментальных) исследованиях, то нетрудно найти коэффициенты a и b. Пусть значению D1 соответствует частость qe,1, а величине D2 — частость qe,2, тогда эти коэффициенты вычисляются по формулам:
b = (qe,1/ D1 -qe,2/ D2)/( D1- D2),
a = (qe,1- b D12)/ D1 или a = (qe,2- b D22)/ D2 . (5.11)
Величина дозы, соответствующая значению частости риска qe, находится из квадратного уравнения, следующего из выражения (5.10):
bD2 + aD – qe = 0 ,
D = (- a ±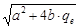 
)/2b. (5.12)
Пример 5.5. В процессе выявления профессионального риска, связанного с воздействием некоторого токсиканта, фиксировались случаи патологических изменений в двух группах персонала, испытавших раз-ные дозовые нагрузки. Первая группа риска насчитывала 100 человек, каждый из которых получил дозу токсиканта, равную 0,1 мг. В этой группе было отмечено 11 случаев патологии, в то время как число ожидавшихся случаев этой патологии предполагалось равным 9. Во второй группе риска было 80 человек, каждый из них получил дозу, равную 0,5 мг. Число патологических нарушений, зафиксированных в этой группе, составило 18 против 10 ожидавшихся. Требуется определить коэффициенты зависимости (5.5) и найти дозу, при которой частость дополнительного риска равна 0,1.
В данной задаче Nt,1 = 100, D1 = 0,1 мг, Nt,2 = 80, D2 = 0,5 мг, Et,1 = 11, Eс,1 = 9, E t,2 = 18, E с,2 = 10. Условия задачи позволяют вычислить частости дополнительного риска для каждой из исследованных групп:
qe,1 =(qt,1- qc,1)/(1- qc,1)=[(E t,1/Nt,1)-(Eс,1 /Nt,1)]/(1- E с,1 /Nt,1) =
= [(11/100)-(9/100)]/(1-9/100) = 0,022,
qe,2=(qt,2- qc,2)/(1- qc,2)=[(E t,2/Nt,2)-(E с,2/Nt,2)]/(1- E с,2/Nt,2) =
= [(18/80)-(10/80)]/(1-10/80) = 0,114.
Коэффициенты b и a определяются с помощью выражений (5.11):
b = [0,022/0,1 -0,114)/0,5]/(0,1 - 0,5) = 0,02,
a = (0,022 - 0,02×0,01)/0,1 = 0,22.
Следовательно, линейно-квадратичная модель зависимости частости риска от дозы в данном случае имеет вид:
qe = 0,22D +0,02D2.
Значение дозы, соответствующее заданной частости риска qe = 0,1, вычисляется по (5.12):
D = [–0,22 ±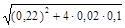 
] / (2·104),
D1= 0,42 мг, D2 = –11,5 мг.
Квадратное уравнение дает два решения, второе из них надлежит отбросить, поскольку доза не может быть отрицательной. Таким образом, искомое значение дозы D = 0,42 мг.
Линейно-квадратичная модель зависимости частоcти риска от дозы значительно меняется при малых и больших значениях D. При малых дозах снижается вклад квадратичного слагаемого (если a > 0 и b > 0), и уравнение (5.10) может быть представлено в линейной форме:
qe = a D .
При больших дозах уравнение (5.10) приводит к завышенным результатам, это можно скорректировать введением экспоненциального сомножителя:
qe = (aD + bD2)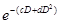 
. (5.13)
Полученная зависимость называется линейно-квадратично-экспоненциальной (модель ЛКЭ). Коэффициенты с и d, как и коэффициенты a и b, находятся из экспериментальных исследований. Для этого приходится решать систему из четырех уравнений, что требует применения компьютера.
Модель ЛКЭ используется, например, в радиобиологических исследованиях для описания зависимости между дозой ионизирующего излучения и вызванными ею последствиями (гибель клеток, хромосомные аберрации, появление злокачественных новообразований и т.д.). При малых дозах радиации справедлива линейная модель, с увеличением дозы становится существенным вклад квадратичного члена, а при еще больших значениях дозы количество наблюдаемых негативных эффектов снижается. Это объясняется тем, что при таких дозах многие клетки погибают и, следовательно, не участвуют в продуцировании фиксируемых последствий. Экспоненциальный сомножитель отражает количество клеток, еще оставшихся живыми после получения данной дозы излучения. Сначала начинает сказываться линейная часть экспоненциального спада, а затем и квадратичная.