Материалы по контролю и оценке учебных достижений обучающихся

1) Семестровое задание № 1 (смотри п. 10, задание для СРС 3-7).

2) Семестровое задание № 2 (смотри п. 10, задание для СРС 12, 19-21).

3) Примерный вариант контрольной работы № 1.

Контрольная работа № 1

Вариант – 0

1. С помощью равносильных преобразований установите тождественную истинность формулы: .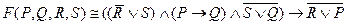

2. Для истинностной функции 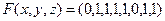найдите формулу, её порождающую, в виде СДНФ и СКНФ.

3. Методом от противного выясните, верно ли логическое следование: .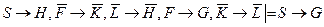

4. Найдите все такие не равносильные между собой формулы , чтобы следующая формула была тавтологией: .

5. Применяя только основные правила вывода и аксиомы, докажите: .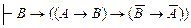

6. Используя обобщённую теорему дедукции и основные правила вывода, докажите: .

7. Докажите выводимость из гипотез, используя определение этого понятия: .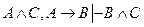

8. Докажите выводимость из гипотез методом резолюций: .

4) Примерный вариант контрольной работы № 2.

Контрольная работа № 2

Вариант - 0

1. Проверить, будет ли верно логическое следование: .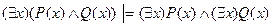

2. Дана формула: 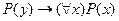. Покажите, что:

а) каждая интерпретация формулы на одноэлементном множестве даёт истинное высказывание;

б) интерпретация формулы на двухэлементном множестве не всегда даёт истинное высказывание.

3. Докажите, что формулы :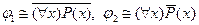

а) равносильны на одноэлементном множестве;

б) не равносильны на двухэлементном множестве.

4. Докажите, что формулы являются общезначимыми:

а) ;

б)

5. Для формулы найдите:

а) приведённую форму;

б) предварённую нормальную форму.

6. Запишите на языке АП высказывания:

а) существует точно два различных 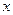таких, что ;

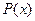б) все параллелограммы являются ромбами.

7. Проанализируйте рассуждения на предмет их правильности. Для этого выявите логические схемы, на которых они основаны, и выясните, справедливы ли они.

а) Все люди смертны. Сократ – человек. Следовательно, Сократ смертен.

б) Все рациональные числа - действительные. Все целые числа – рациональные. Следовательно, все целые числа – действительные.

5) Перечень тестовых вопросов для тестирования № 1 (смотри УМП: Акбердин Р.А., Вьялицин А.А. и др. Сборник тестовых заданий по математической логике и дискретной математике. – Петропавловск, СКГУ, 2004, с. 5-18).

6) Перечень тестовых вопросов для тестирования № 2 (смотри УМП: Акбердин Р.А., Вьялицин А.А. и др. Сборник тестовых заданий по математической логике и дискретной математике. – Петропавловск, СКГУ, 2004, с. 26-37).

Вопросы к коллоквиуму № 1

Модуль 1

1. Логика. Интуиция. История математической логики.

2. Высказывания. Виды. Логические операции над высказываниями.

3. Формулы АВ. Правила записи формул. Классификация формул АВ.

4. Основные тавтологии АВ. Правила получения тавтологий.

5. Равносильность формул АВ. Признак равносильности формул АВ. Основные равносильности формул АВ.

6. Формула двойственная к данной формуле. Закон двойственности формул АВ.

7. Проблема разрешимости формул АВ. Нормальные формы формул АВ: ДО, КО, ДНФ, КНФ. Критерии тождественной истинности и ложности формул АВ. Решение проблемы разрешимости формул (алгоритм).

8. Представление истинностных функций формулами АВ. Истинностная функция. СДНФ и СКНФ. Алгоритмы построения СДНФ, СКНФ. Теоремы о существовании и единственности СДНФ, СКНФ.

9. Алгоритмы перехода от СДНФ к СКНФ, и наоборот. Алгоритмы перехода от ДНФ к КНФ, и наоборот.

10. Алгоритмы перехода от ДНФ к СДНФ, перехода от КНФ к СКНФ

11. Логическое следствие, следование. Признак логического следования.

12. Теорема дедукции, обобщённая теорема дедукции, обратные к ним.

13. Правила логических умозаключений.

14. Приложения АВ к логико-математической практике: анализ рассуждений, упрощение систем высказываний, решение логических задач, нахождение всех следствий из посылок, посылок для следствий, недостающей посылки в рассуждении.

15. Приложения АВ к логико-математической практике: строение и виды теорем. Применение терминов необходимо и достаточно. Виды математических доказательств.

Модуль 2

16. ФАТ. Формальное исчисление; логическое исчисление. Метатеория.

17. Этапы построения ФАТ.

18. Алфавит ИВ. Слово ИВ.

19. Формула ИВ. Правила записи формул ИВ.

20. Аксиоматика ИВ. Эффективно аксиоматизируемая ФАТ.

21. Теорема, вывод ФАТ. Длина доказательства. Доказательство.

22. Формальное определение подстановки.

23. Выводимая из гипотез формула ИВ.

24. Эквивалентные формулы ИВ.

25. Разрешимая ФАТ. ИВ – разрешимая теория?

26. Непротиворечивая ФАТ, содержащая знак «отрицание». ИВ - непротиворечивая теория?

27. Непротиворечивая ФАТ. ИВ - непротиворечивая теория?

28. Полная в широком смысле ФАНТ. ИВ - полная теория?

29. Полная в узком смысле ФАНТ. ИВ - полная теория?

30. Независимость аксиомы ФАНТ. Независимость системы аксиом ФАНТ. Система аксиом ИВ – независима?

31. Алгоритм доказательства независимости аксиом II-IV групп ИВ.

32. Основные правила вывода ИВ.

33. Теорема о свойствах выводимости из гипотез (5 пунктов) .

34. Теорема дедукции и обратная к ней. Обобщённая теорема дедукции и обратная к ней.

35. Вспомогательные правила вывода ИВ.

36. Теорема о связи теорем ИВ и тавтологий АВ.

37. Теорема о связи выводимости из гипотез ИВ и логического следования АВ.

38. Теорема о связи эквивалентности формул ИВ и равносильности формул АВ.

39. Теорема - основные эквивалентности формул ИВ.

40. Теорема - обоснование метода резолюций.

41. Резольвента. Резолютивный вывод.

42. Теорема о полноте метода резолюции.

43. Алгоритм доказательства выводимости из гипотез методом резолюций.

Вопросы к коллоквиуму № 2

Модуль 3

1. Предикат. Область определения и область истинности.

2. Классификация предикатов.

3. Логические операции над предикатами.

4. Теоремы о том, как находятся области истинности предикатов, являющихся конъюнкцией предикатов, дизъюнкцией предикатов, импликацией предикатов, эквиваленцией предикатов от одних и тех же переменных, определённых на одном и том же множестве.

5. Кванторные операции над предикатами. Свободные и связанные переменные.

6. Алфавит АП.

7. Формула АП.

8. Открытая и замкнутая формулы АП.

9. Интерпретация формул АП.

10. Классификация формул АП: тождественно истинная на М, тождественно ложная на М, выполнимая на М.

11. Общезначимая формула, тождественно ложная формула АП.

12. Равносильные формулы АП.

13. Закон пронесения квантора общности через операцию «конъюнкция». Закон пронесения квантора существования через операцию «дизъюнкция». Законы коммутативности кванторов. Законы де Моргана для кванторов. Закон удаления квантора общности. Закон введения квантора существования.

14. Приведённая форма, предварённая нормальная форма.

15. Логическое следование формул АП. Признак логического следования.

16. Приложение АП к логико-математической практике. Задачи записи на языке АП. Анализ правильности рассуждений. Примеры.

17. Аристотелева силлогистика. Основные типы суждений Аристотелевы силлогизмы. Верные, неверные силлогизмы.

Модуль 4

18. ИП - этапы построения.

19. Алфавит ИП.

20. Формулы ИП.

21. Аксиомы ИП.

22. Основные правила вывода ИП.

23. Связь ИП с АП. Теорема о связи теорем ИП и общезначимых формул АП.

24. Непротиворечивость ИП.

25. Полнота ИП в широком, узком смысле.

26. ИП с равенством - этапы построения.

27. Узкое ИП, расширенное ИП.

28. ИП 1-го порядка. ИП 2-го порядка. Формальные теории 1-го порядка.

Модуль 5

29. Формальная арифметика - этапы построения.

30. Теорема Геделя о неполноте.

9) Перечень тестовых экзаменационных вопросов (смотри УМП: Акбердин Р.А., Вьялицин А.А. и др. Сборник тестовых заданий по математической логике и дискретной математике. – Петропавловск, СКГУ, 2004, с. 5- 41).