Элементарные логические функции

Одним из основных понятий в математической логике является понятие высказывания. Под высказыванием понимается всякое предложение, относительно которого имеет смысл утверждать о его истинности или ложности. Например, 8 - четное число, 2 больше 10, сегодня воскресенье, и т.д.

Из простейших высказываний путем соединения их с помощью логических связок можно составлять новые, более сложные высказывания. Истинность или ложность новых высказываний определяется истинностью или ложностью составляющих высказываний и тем, какими логическими связками они соединены.

Абстрагируясь от конкретного содержания высказывания можно рассматривать его как некоторую величину, которая может иметь какое-либо одно значение из двух возможных значений: истина или ложь. При этом сложное высказывание, составленное из простых высказываний, в математической логике рассматривается как некоторая функция от высказываний-аргументов. Множество значений, которые может принимать функция, тоже состоит из двух элементов: истина и ложь.

В дальнейшем высказывания будем обозначать прописными буквами латинского алфавита. Значение истинности обозначают через 1, а значение лжи через 0.

Логика, которая оперирует лишь с объектами (высказывания, функции), принимающими одно из двух возможных значений, называется двузначной или булевой. Простые высказывания называются логическими или булевыми переменными, а их функции - логическими или булевыми функциями, либо функциями алгебры логики (ФАЛ).

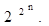Булева функция, зависящая от n аргументов, называется n-местной и является полностью заданной, если указаны ее значения для всех наборов значений аргументов. Так как число возможных значений каждого аргумента равно 2, то при числе аргументов nколичество различных наборов значений аргументов равно 2ⁿ. Каждому набору может соответствовать одно из двух возможных значений функций. Следовательно, количество различных булевых функций от nпеременных равно

Функции одной и двух логических переменных называются элементарными.

Логические функции одной переменной. Для одной переменной число функций равно 4. Все эти функции F₁, F₂, F₃, F₄ представлены в таблице 1, которая называется таблицей истинности логических функций. Значение функций F₁ и F₂ не

зависят от значения аргумента X . Это константы F₁=1 и F₂=0. Значение функции F₃ повторяют значения аргумента X, F₃ = X. Нако-нец, значения функции F₄ противоположны значениям аргумента.

Функции F₁, F₂, F₃ являются тривиальными и практического интереса не представляют. Функция F₄ называется отрицанием или инверсией и обозначается .

Таблица 2.

X					Название функции	Обозначение	«Замечательные» свойства
Y
					Константа		Х			Х	Х
					Стрелка Пирса	X¯Y
					Запрет по Y	XDY	X
					Инверсия Y		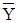		X		X
					Запрет по Х	YDX	X
					Инверсия Х				Х		Х
					Сумма по модулю 2	ХÅY	X				X
					Штрих Шеффера	X/Y
					Конъюнкция, умножение	X×Y, XÙY X&Y	X	X		X
					Эквивалентность	X~Y		X
					Переменная Х	Х	Х	Х	Х	Х	Х
					Импликация от Y к Х	Y®X		X
					Переменная Y	Y	X	X	X	X	X
					Импликация от Х к Y	X®Y		X
					Дизъюнкция, сложение	X+Y, XÚY	X	X		X
					Константа 1			Х		Х	Х

Логические функции двух переменных. Для двух переменных число всех возможных функций равно 2⁴ = 16 . Полный набор функций двух переменных, их обозначения и названия приведены в табл.2. Из таблицы видно, что восемь функций могут быть получены из других восьми путем применения операции отрицания.

Некоторые логические функции обладают определенными свойствами, получившими название “замечательные” свойства. Всего различают пять “ замечательных” свойств. В табл.2 эти свойства отмечены номерами: 1- свойство сохранять нуль, 2- свойство сохранять единицу, 3- самодвойственность, 4-монотонность, 5-линейность. Более подробно об этих свойствах сказано дальше.