Клаузу необходимо доказать следующими методами: аксиоматическим, натурального исчисления, резолюции и Вонга.
Максимально упростите выражение, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните упрощенное выражение с исходным.
Решение:
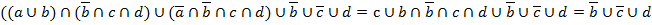
Преобразования:
1. По дистрибутивному закону 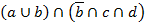
2. По закону поглощения 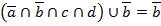
3. По закону противоречия 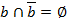
4. По закону поглощения 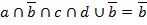
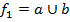
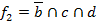
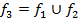
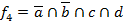
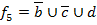
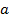 | 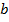 | 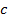 | 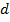 | 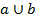 | 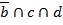 | 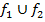 | 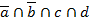 | 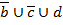 | 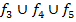 | 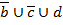 |
Следственно, преобразование выполнено, верно!
Задание 2:
Докажите аналитическим путем справедливость выражения
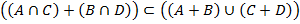
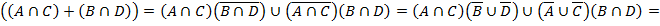
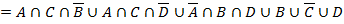
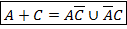 – по этому закону все «+» раскрыты
– по этому закону все «+» раскрыты
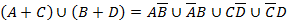
Таким образом, видим, что конституэнты единицы левой части состоят из 3-х множеств, два из которых совпадают с конституэнтами выражения правой части.
Таким образом, можем сделать вывод, что правая часть выражения включает в себя левую часть, т.е. множество правой части включает множество левой.
Задание 3.
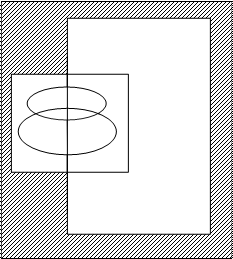
Представить заштрихованные и не заштрихованные области аналитическими выражениями
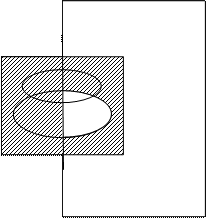

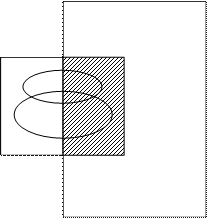
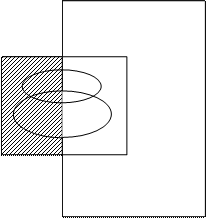 Разобьем заштрихованные части на отдельные области:
Разобьем заштрихованные части на отдельные области:
1)  2) 3)
2) 3)
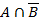
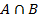
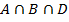
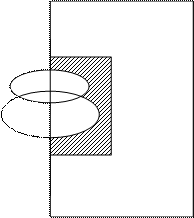
 4) 5)
4) 5)
 |
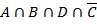
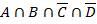
Объединим 1, 4, 5:
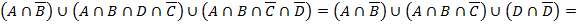
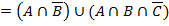
Разобьем не заштрихованную область на отдельные части:
1. 

 2) 3)
2) 3)
 |
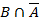
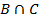
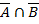
Объединим области: 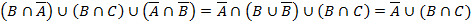
Иначе заштрихованная область: 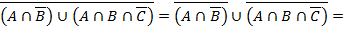
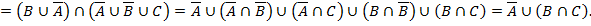
Минимизация: каждая клетка с «1» соответствует конституэнте. По закону склеивания смежные конституэнты объединяют для получения импликанты 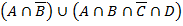 . Все конституэнты заштрихованной области записаны сюда, потом 4 склеены в
. Все конституэнты заштрихованной области записаны сюда, потом 4 склеены в 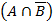
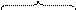 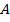 | 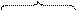 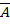 | ||||
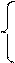 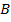 | 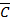 | ||||
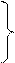 | 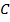 | ||||
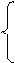 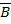 | |||||
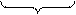 1 1 | 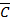 | ||||
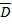 |   |  |
 | 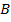 | 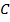 | 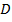 | 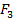 | 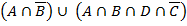 | 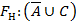 | 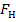 | 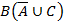 |
Задание 4
Клаузу необходимо доказать следующими методами: аксиоматическим, натурального исчисления, резолюции и Вонга.
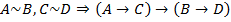
Метод натурального исчисления:
1. 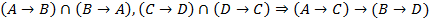 (1, уравнение эквивалентности, УЭ)
(1, уравнение эквивалентности, УЭ)
2. 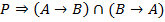 (1, базовое правило, БП)
(1, базовое правило, БП)
3. 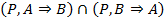 (2, УЭ)
(2, УЭ)
4. 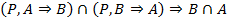 (3, правило введения конъюнкции, ВК)
(3, правило введения конъюнкции, ВК)
5. 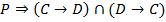 (1, БП)
(1, БП)
6. 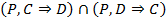 (5, УЭ)
(5, УЭ)
7. 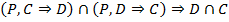 (6, ВК)
(6, ВК)
8. 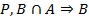 (4, удаление конъюнкции, УК)
(4, удаление конъюнкции, УК)
9. 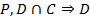 (4, УК)
(4, УК)
10. 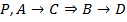 (удаление импликации, УИ)
(удаление импликации, УИ)
11. 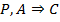 (10, УИ)
(10, УИ)
12. 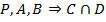 (ВК)
(ВК)
13. 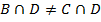 Следственно клауза не верна
Следственно клауза не верна
Аксиоматичный метод:
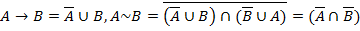
Подставим в выражение, получим
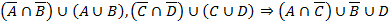
Воспользуемся законом дистрибутивности, заменим «,» на « 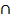 »
»
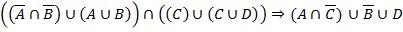
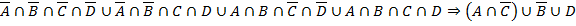
Метод Вонга
Доказательство сводится к последовательному разбиению дизъюнктов или конъюнктов, чтобы прийти к виду 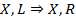
( 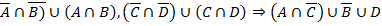
1. 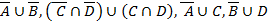
1.1. 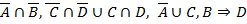
1.1.1. 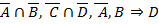 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
1.1.2. 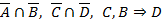 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
1.1.2.1. 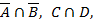
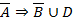
1.2. 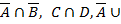
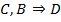
1.2.1. 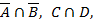
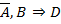 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
1.2.2. 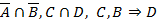 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
2. 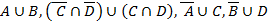
2.1. 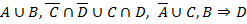
2.1.1. 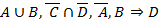 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
2.1.2. 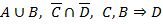 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
2.1.2.1. 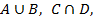
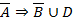
2.2. 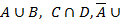
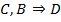
2.2.1. 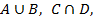
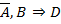 не удовлетворяет клаузе Вонга
не удовлетворяет клаузе Вонга
2.2.2. 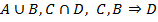 не удовлетворяет клаузе Вонга, так как не смогли представить в виде
не удовлетворяет клаузе Вонга, так как не смогли представить в виде 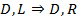
Следственно, клауза не верна!
Метод резолюции
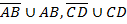 ,
, 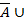
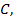
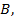
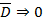
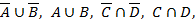
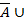
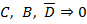
1 2 3 4 5 6 7
8.
|
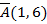
9. 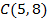
10. 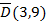
11. 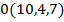
Задание 5.
Ниже приведена легенда. Записать клаузу, отвечающую тексту или контексту легенды, с использование 4-6 различных букв. С помощью таблицы истинности найдите МНФ, минимальное и транверсальные покрытия.
A - Есть материалы
B - Есть станок
C - Изготовить партию фальшивых денег
D - Милиция хорошо работает
E - Высокая заработная плата милиционера
F - Высокая сознательность
Посылки:
Если будут и материалы и станок, то преступник изготовит партию фальшивых денег
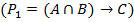
Если хорошо работает милиция, то фальшивых денег не появиться 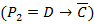
Милиция хорошо работает тогда и только тогда, когда получает высокую зарплату
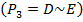
Заключение:
Пока высокой зарплаты нет, но есть высокая сознательность милиции и нет преступлений
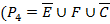 )
)
Клауза:
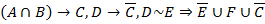
Таблица истинности
| n | A | B | C | D | E | F | 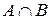 | P1 | P2 | P3 | P | P4 |
СДНТ: 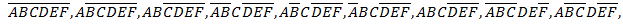
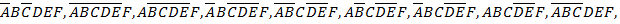
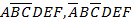
Это конституанта истинного предиката , т.е. где «1» в столбике Р записывается соответственно ABCDEF, если 0 – то 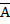 , если 1- то А
, если 1- то А
МНФ: букв, кот. есть в каждой СДНТ – нет, следовательно МНФ = 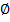
Минимальное покрытие: покрытие с наименьшим числом термов 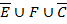
Трансверсальное покрытие включает все имеющиеся термы:
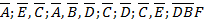

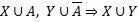 2.
2. 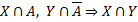 Выражения в скобках попарно рассматриваются и сворачиваются по правилу 1 или 2 (n) – номер используемых дизъюнктов
Выражения в скобках попарно рассматриваются и сворачиваются по правилу 1 или 2 (n) – номер используемых дизъюнктов