I.I3. Погрешности косвенных измерений

При косвенных измерениях значение искомой физической величи­ны находят путем согласованных измерений других величин, связанных с измеряемой величиной известной функциональной зависимостью. Эти другие величины будем называть измеряемыми аргументами. Значения аргументов чаще всего находят в результате прямых измерений, но иногда – в результате совместных, совокупных или косвенных измере­ний. Поэтому возникает задача: определить погрешности функции при данных погрешностях аргументов.

Измеряемая величина Q связана с измеряемыми аргументами 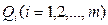зависимостью

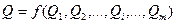(1.48)

Встречаются случаи неявной зависимости между Q и Q_i.

По виду функциональной зависимости различают косвенные из­мерения с линейной зависимостью между измеряемой величиной и аргументами

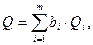
с нелинейной зависимостью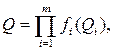

с зависимостью смешанного типа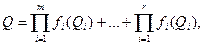

где b_i - постоянный коэффициент i-го аргумента Q_i
m , r - числа слагаемых.

Оценим результат 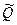и погрешности D косвенного измерения,
имея оценки результата 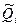и погрешности D_i прямых измерений каж­дого из аргументов.

Пусть каждый из аргументов Q_i характеризуется оценкой 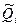и погрешностью 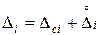, которая представляет собой некоторую реализацию суммарной погрешности i -го аргумента. Подставим в уравнение косвенного измерения величину 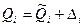и разложим его в ряд Тейлора. Пренебрегая членами со степенями выше первой, имеем

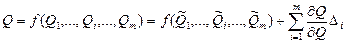(1.49)

Из уравнения (1. 49) получаем оценку результата

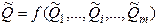(1.50)

и погрешности косвенного измерения

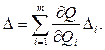
Допустимость такой оценки должна быть проверена. Производные 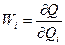называют коэффициентами влияния, а слагаемые 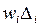- частными погрешностями.

Рассмотрим случайные погрешности. При этом систематические составляющие погрешностей оценок всех Q_i будем считать постоянны­ми. Выразим оценку среднего квадратического значения случайной погрешности результата косвенного намерения как

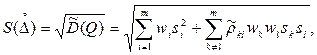(1.51)

где 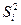– оценка дисперсии результата прямого измерения i-го аргумента,

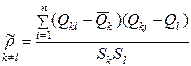– оценка коэффициента корреляции между случайными погрешностями измерения аргументов k и l 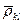лежит в интервале ±I.

Когда измерения аргументов производятся не одновременно, различными средствами измерений, то коэффициент корреляции близок к нулю, и

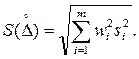(1.52)

Введенным новым обозначением оценки среднего квадратического подчеркивается, что в уравнениях используются дисперсии результа­тов наблюдения при прямых измерениях аргументов.

Постоянная систематическая погрешность Δ_с результата косвен­ного измерения

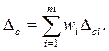(1.53)

Если знаки частных систематических погрешностей D_ci неиз­вестны, то систематическую погрешность результата косвенных изме­рений находят как

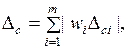(I.54)

которую называют предельной.

При расчете относительных погрешностей d_сист d_сл выражения для D_с и 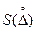относят к результату косвенных измерений Q.

Следует отметить, что относительная погрешность косвенных из­мерений в некоторых случаях может приобретать очень большие значе­ния, например, для функцией вида Q=Q₁-Q₂ при малых значениях разности .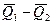

При косвенных измерениях необходимо разрабатывать такие мето­ды, которые обеспечивают сохранение в допустимых пределах погреш­ности косвенного измерения. Это достигается выбором значений Q_{l и} Q_k, при которых относительная погрешность не выходит за пре­делы допустимой; применением способов измерения, при которых урав­нение косвенного измерения не содержит малых разностей; разработ­кой методов и средств измерений, обеспечивающих прямое измерение вместо косвенного.

Рассмотрим, как оценивается доверительный интервал случайной погрешности и границы или доверительный интервал не исключенных систематических погрешностей результата косвенных измерений.

Случайную погрешность результата косвенного измерения мож­но считать нормально распределенной случайной величиной даже в том случае, если слагаемые имеют распределение, отличное от нор­мального, но число слагаемых не менее 4 -5 и отсутствует домини­рующая погрешность.

Доверительные границы e_p случайной погрешности определяют по формуле

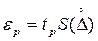(1.55)

Коэффициент 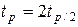, где 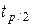находится по функции Лапла­са (табл.2 приложения).

Как говорилось выше, не исключенные систематические погреш­ности можно рассматривать как величины случайные. Для каждой из составляющих находят границы Q_i и, если возможно обосновать за­кон распределения и оценить 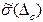, определяют их как

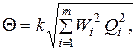(I.56)

где k- коэффициент, определяемый принятой доверительной веро­ятностью, который при доверительных вероятностях 0,9; 0,95; 0,99 принимают соответственно равным 0,95; 1,1; 1,4.

Границы суммарной погрешности измерений оценивают в соответствии с ГОСТ 8.207-76 [7].