Логические методы ускорения умножения

1. умножение на два разряда множителя за один такт:

b_n b_n+1 микрооперация

0 0 нет

0 1 +А

1 0 +2А

1 1 -А

Bn	bn+1	P	мко	P'
			-
			+A
			+A
			+2A
			+2A
			-A
			-A
			-

В базовом алгоритме Т_умн= n(Т_сдв+0,5Т_сум).

В этом алгоритме Т_умн=n/2(Т_сдв+3/4Т_сум).

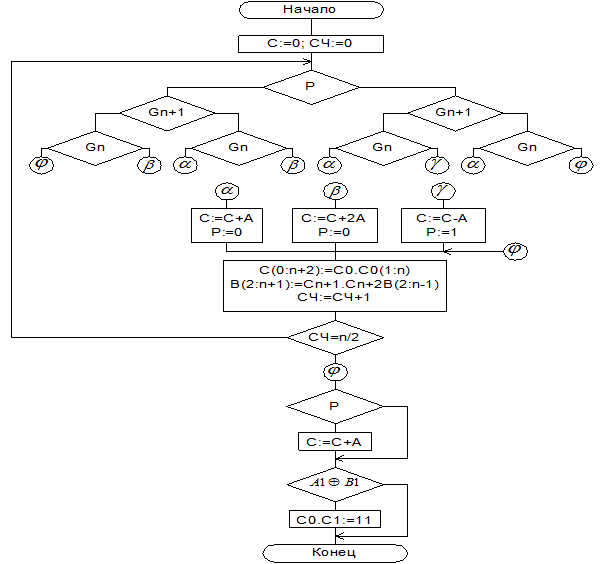
Микропрограмма умножения на два разряда множителя.

При прибавлении к сумме частных произведений n+1 разрядного частного произведения 2А,. Результат может получиться n+2 разрядным. С учетом разряда переноса и знакового разряда сумматор должен быть n+3 разрядным, предполагается, что n – четное.

В качестве аппаратной поддержки необходим формирователь дополнительного кода, чтобы вычесть А.

2. умножение с последовательным преобразованием цифр множителя.

В …01111110…

+А -А

…1 0 1 0 1 0 1 0 1… (*)

-А+А-А+А-А+А-А+А-А

Для приодаления ситуации (*) договорились игнорировать серии длиной в 1 бит. Для реализации микропрограммы умножения вводится триггер j, который задает режим сдвига, и тогда возможны 4 ситуации:

j=0 – сдвиг по 0ж

j=1 – сдвиг по единицам.

1) начало серии единиц

j=0

b_n+1=1

b_n=1

-A j:=1

2) начало серии нулей

j=1

b_n+1=0

b_n=0

+A j:=0

3) единица среди нулей

j=0

b_n+1=1

b_n==0

+A j=0(без изм.)

4) ноль среди единиц

…111101111…В

j=1

b_n+1=0

b_n=1

-A j=1(без изм.).

В начале алгоритма j:=0. сдвиг осуществляется на первый разряд. Цикл проверки b_n, b_n+1, p повторяются n раз. Если при выходе из цикла j=1, то делается дополнительное суммирование С:=С+1.

№	bn	bn+1	j	M\o	j’
				-
				+A
				+A
				-
				-
				-A
				-A
				-

Пример:

В = 0 1 1 0 1 1 1 0 1 0 1 1 1

+А - - -А - - - -А - -А - - -

Т_умн.=n*(Т_сдв+1/3Т_сум.);

Для ускорения алгоритма можно ввести цепи сдвига на 2 разряда. При встречи комбинации, описанной в 4 и 5 строках, выполнить микрооперацию сдвига на 1 разряд, для остальных – на 2 разряда.