Реализация методов гистограммных преобразований в системе MATLAB

Благодаря своей высокой эффективности методы гистограммных преобразований нашли широкое применение при решении задач обработки изображений. Этим объясняется существование большого количества методов класса гистограммных преобразований, что позволяет решать широкий круг задач с учетом разнообразных нюансов. Методы данного класса бывают глобальными и локальными (или еще их называют скользящими). Глобальные методы гистограммных преобразований являются, в сущности, табличными методами. Поэтому основное их преимущество состоит в быстродействии. Однако, глобальные методы не используют при преобразовании характеристик локальных областей изображения, поэтому они не обеспечивают эффективную обработку тонкоструктурных областей. Для более детальной обработки изображений используют скользящие методы. Они обеспечивают качественное контрастирование мелких деталей изображения. Вместе с тем, они более объемны по вычислительным затратам. Поэтому при использовании методов класса гистограммных преобразований нужно искать компромисс между качеством и быстродействием обработки изображений.

Основным этапом при создании методов гистограммных преобразований является корректное построение гистограммы распределения яркостей элементов изображения. Для этого в большинстве случаев используются встроенные функции hist, imhist. В Matlab V.4.x функция построения гистограммы яркостей элементов изображения работает некорректно, однако этот недостаток устранен в последующих версиях.

Приведем пример алгоритма построения гистограммы изображения, который использовался в Matlab V.4.x:

% Считывание изображения из файла
fid=fopen('F:\MATLAB\len.img','r');
[A,count]=fread(fid,'char');
fclose(fid);
L1=min(A);L2=max(A);t=length(A);
% Определение границ диапазона воспроизводимых яркостей
H=[];
for L=L1:L2;
disp(L); H(L)=0;
for k=1:t; if A(k)==L; H(L)=H(L)+1; end; end;
end;
plot(H);

Приведем пример реализации классического метода эквализации (выравнивания) гистограммы распределения яркостей элементов изображения.

% Считывание изображения из файла
fid=fopen('F:\MATLAB\len.img','r');
[A,count]=fread(fid,'char');
fclose(fid);
A=A'; N=256; M=N;
A=A(1:N*M); A=A+1;
H=hist(A,max(A)-min(A)+1);
Hps=zeros(1,256-(max(A)+1)); Hdo=zeros(1,min(A));
H=[Hdo,H,Hps];
for i=1:256;
disp(i);
S(i)=sum(H(1:i));
end;
K=255/(M*N);
A1=K.*S(A);
A1=fix(A1);% Массив изображения с эквализованной гистограммой

С выходом новых версий системы Matlab необходимость в создании программ построения гистограммы изображения и ее эквализации исчезла. Эти программы заменили встроенные функции imhist и histeq, которые применяются для построения и эквализации гистограммы изображения.

Обзор методов цифровой обработки изображений: Метод преобразования локальных контрастов

Одной из наиболее удобных форм представления информации является изображение. Существуют различные подходы к визуализации. Одним из существенных недостатков этих методов является то, что в большинстве своем они обеспечивают формирование слабоконтрастных изображений. Это вызывает необходимость развития методов их обработки. Поэтому основная цель методов улучшения состоит в преобразовании изображений к более контрастному и информативному виду. Довольно часто на изображении присутствуют искажения в определенных локальных областях, которые вызваны дифракцией света, недостатками оптических систем или расфокусировкой. Это порождает необходимость выполнения локальных преобразований изображения.

Рассмотрим известную технологию повышения качества изображений, которая основывается на преобразовании локальных контрастов [1, 2]. Основная ее идея состоит в том, что для каждого элемента изображения сначала определяется локальный контраст, а потом происходит его нелинейное усиление и восстановление яркости данного элемента изображения из уже скорректированного локального контраста. Основные шаги реализации метода представлены на рис. 1 в виде структурной схемы.

Рис. 1. Структурная схема метода усиления локальных контрастов.

На первом этапе выбирается элемент 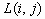с координатами 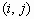исходного изображения , .

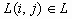На втором этапе вычисляется локальный контраст элемента по предложенной в работе [2] формуле

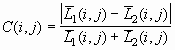, (1)

где

, (2)

, (3)

а , 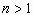. Област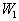и и представляют собою скользящие окна в виде квадрата с центром в элементе с координатами 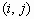. Скользящее окно 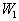размещено внутри скользящего окна .

Следует отметить, что форма и размеры скользящего окна, в общем случае, могут быть произвольными. В большинстве методов размеры апертуры остаются постоянными на протяжении реализации всего метода. Однако существуют методы обработки изображений с адаптивным скользящим окном [3]. Известно, что степень обработки сигналов зависит от размеров апертуры фильтра, а именно при малом размере апертуры фильтра операции усреднения подвергается меньшее число значений, что обеспечивает лучшее сохранение контрастных деталей сигнала. Но при этом шум будет сглажен хуже. И наоборот, при большом размере апертуры фильтра сглаживание шума будет происходить лучше, но при этом возможна "потеря" некоторых контрастных деталей, присутствующих в исходном сигнале. Итак, становится ясным, что качество обработки изображения можно улучшить путем выбора наиболее подходящих размеров апертуры. К сожалению, реальные изображения не являются стационарными: они содержат как монотонные области, так и изображения перепада, поэтому на практике очень трудно подобрать оптимальные размеры апертуры фильтра. В подобных ситуациях качество обработки можно улучшить, если использовать апертуру с большими размерами в монотонных областях обрабатываемого изображения и апертуру с малыми размерами вблизи областей перепада.

Третий этап рассматриваемого метода состоит в нелинейном усилении локального контраста

, (4)

где 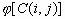- нелинейная монотонная функция, которая удовлетворяет условиям

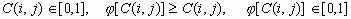. (5)

Функция 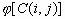является монотонно возрастающей и определенной на промежутке 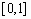. За функции 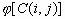принимаются степенные, экспоненциальные, логарифмические и гиперболические функции. Реальные изображения имеют различную природу происхождения и разнообразное семантическое наполнение. Исходные локальные контрасты в тех или иных областях изображения также разные. В некоторых областях они достаточны, а в некоторых потенциально информативных областях их нужно усиливать. Исходя из этого, функции преобразования локальных контрастов бывают двух видов - условно "постоянные" и адаптивные. "Постоянные" обеспечивают одинаковое усиление локальных контрастов в каждой точке изображения. Адаптивные функции преобразования локальных контрастов проводят преобразование (усиление) локальных контрастов в зависимости от характеристик локальных областей. Такой подход обеспечивает более эффективное улучшение изображений с точки зрения их визуального восприятия.

На четвертом этапе происходит восстановление элемента изображения с координатами 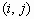и скорректированного контрастом . Для этого используют выражение, которое определяется из выражения (1) определения локальных контрастов

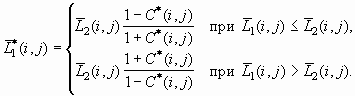(6)

Расчет с помощью выражений (1) - (6) проводят для каждого элемента изображения .

Экспериментальные исследования и компьютерное моделирование данного метода показали его недостаточную эффективность, поскольку при таком подходе результирующее изображение получается размытым. Для устранения этого недостатка в работах [2, 4, 5] предложено использовать вместо усредненного значения 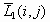значение центрального элемента 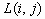. То есть область 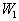вырождается в центральный элемент 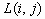и принимает размеры . Учитывая это, в дальнейшем будем считать, что

(7)

и

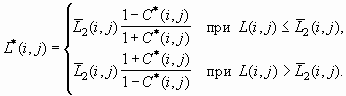(8)

Рассмотренный метод является классическим примером методов класса преобразования локальных контрастов. Эти методы позволяют решать задачи не только улучшения визуального качества изображений, но и реализовывать как высокочастотную, так и низкочастотную фильтрацию с помощью применения различных функций преобразования локальных контрастов.

Литература