Нечеткие множества и их особенности

Нечёткое (или размытое, расплывчатое) множество — понятие, введённое Л. Заде, который расширил классическое (канторовское) понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.

Определение: нечеткое множество (a fuzzy set)

Пусть C есть некоторое универсальное множество (универсум). Тогда нечеткое множество A в C определяется как упорядоченное множество пар

A= ,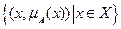

где 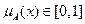называется функцией принадлежности (ФП) элемента х к нечеткому множеству A.

ФП приписывает каждому элементу из C значение из интервала [0, 1], которое называется степенью принадлежности х к A или нечеткой мерой.

Нечеткая мера может быть рассмотрена как степень истинности того, что элемент х принадлежит A.

Определение: основа нечеткого множества (a support of a fuzzyset)

Основой нечеткого множества A является множество всех точек 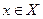таких, что .

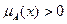Таким образом, определение нечеткого множества является расширением определения классического множества, в котором характеристическая функция может принимать непрерывные значения между 0 и 1. Универсум C может быть дискретным или непрерывным множеством.

Для представления ФП обычно используется несколько типов параметрических функций.

Типовые представления ФП

Треугольные ФП (рис. 2.2, а) описываются тремя параметрами {a, b, c}, которые определяют x координаты трех углов треугольника следующим образом:

.

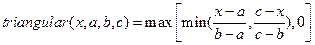Трапециидальные ФП (рис. 2.2, в) описываются четырьмя параметрами {a,b,c,d}, которые определяют x координаты четырех углов трапеции следующим образом:

.

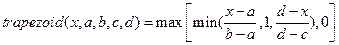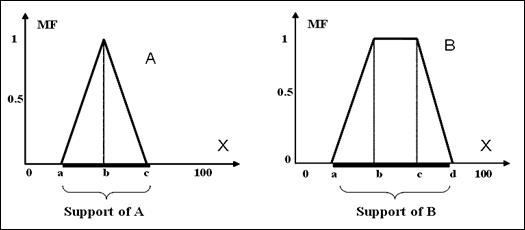
Рис. 2.2. Треугольная и трапецеидальная ФП

Гауссовские ФП (рис. 2.3) специфицируются двумя параметрами и представляют собой следующую функцию: .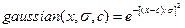

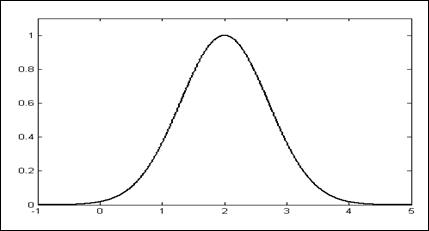
Рис. 2.3. Гауссовская ФП

Лингвистические переменные

Одним из фундаментальных понятий, введенных также Л.Заде, является понятие лингвистической переменной.

Определение: лингвистическая переменная (ЛП) представляет собой следующую пятерку 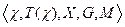, где – имя переменной, 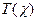– терм-множество, задающее множество значений ЛП, являющихся языковыми выражениями (синтагмами), X – универсум, G – синтаксическое правило, используя которое мы можем формировать синтагмы 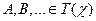, M – семантическое правило, используя которое каждой синтагме 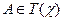приписывается ее значение, являющееся нечетким множеством в универсуме X.

Примером ЛП может служить, например, переменная = «возраст». Ее терм-множество может быть, например, следующим:

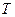(возраст) = {очень молодой, молодой, более или менее молодой, средних лет, старый, очень старый}.

Универсумом для данной ЛП может служить некоторое множество действительных чисел, например, интервал 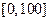. Семантическое правило М приписывает термам из T (возраст) значения, являющиеся различными модификациями нечетких множеств.

Вернемся к нашему примеру управления движением автомобиля и опишем лингвистические значения в выше приведенных правилах с помощью нечетких множеств. Рассмотрим следующие лингвистические переменные:

x – расстояние между машинами;

y – скорость впереди едущей машины;

z – ускорение управляемого автомобиля.

ФП должны быть определены в соответствии с рассматриваемой ситуацией управления. Так, например, скорость равная 70 км/час является «большой» в ситуации движения по городской дороге и может рассматриваться как «небольшая» в ситуации движения по скоростному шоссе.

Определим для нашего примера следующие универсумы:

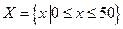[м], 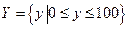[км/час],

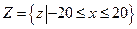[км/час²].

На рис. 2.4 показаны ФП для описания лингвистических значений «небольшая» (slow) и «большая» (fast) для скорости и «близкое» (short) и «большое» (long) для расстояния.

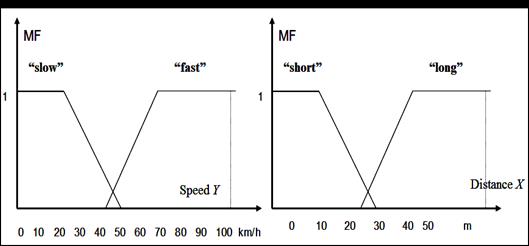
Рис. 2.4. Нечеткие множества для задачи управления простейшим движением автомобиля

Различия между классическим и нечетким представлением множества

Обсудим эти различия с использованием следующего примера. Рассмотрим классическое и нечеткое представления множества для описания лингвистического значения «короткий» (для расстояния).

На рис. 2.5 показаны различия между классическим и нечетким представлением множества A для данного примера.

Рис. 2.5. Классическое и нечеткое представления множества A

Определим классическое представление множества A так, как показано на рис. 2.5 слева. В этом случае характеристическая функция будет:

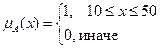
Нечеткое представление множества A показано на рис. 2.5 справа. В этом случае функция принадлежности ФП выглядит следующим образом:

.

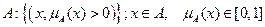Зададим теперь следующий вопрос: принадлежит ли точка 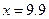м или точка 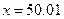м множествуA?

С точки зрения классического представления ответ «нет». С точки зрения человеческого восприятия ответ скорее «да», чем «нет». С точки зрения нечеткого представления ответ «да».

Таким образом, данный простой пример наглядно показывает, что нечеткий подход более близок к естественному, человеческому, и обладает большей гибкостью, нежели классический подход.

С помощью нечетких множеств мы можем описывать нечеткие границы.

Основные операции в теории нечетких множеств

Определим основные нечеткие операции следующим образом.

Определение:нечеткое подмножество (Fuzzy Containment или Fuzzy Subset). Нечеткое множество A содержится в нечетком множестве B (или, эквивалентно, A является подмножеством B) тогда и только тогда, когда 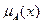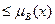для всех 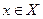. В символьной форме:

.

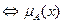
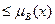Определение:эквивалентность нечетких множеств (Equality of Fuzzy Sets). Эквивалентность (равенство) нечетких множеств A и B определяется следующим образом:

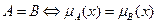для каждого .

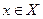Определение:нечеткое объединение или нечеткая дизъюнкция (Fuzzy Union).Объединение двух нечетких множеств A и B (в символьной форме пишется как 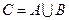или A OR B или A 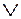B) есть нечеткое множество 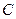, ФП которого определяется следующим образом:

= .

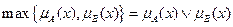Определение:нечеткое пересечение (Fuzzy Intersection).Пересечение двух нечетких множеств A и B (в символьной форме записывается как 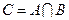, или C = A AND B, или C = A B) есть нечеткое множество 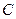, ФП которого определяется следующим образом:

= .

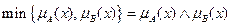Определение:нечеткое дополнение.Дополнение A (в символьной форме пишется как 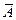или ) есть нечеткое, ФП которого определяется следующим образом:

.

На рис 2.6 показаны примеры нечетких операций над нечеткими множествами.

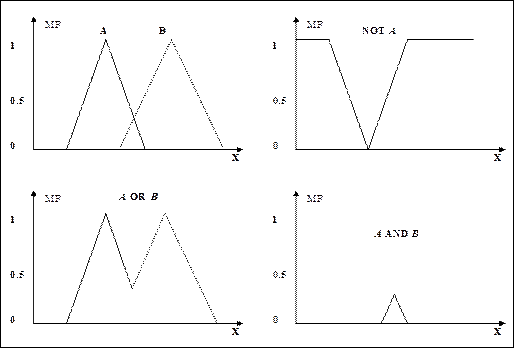
Рис. 2.6. Примеры нечетких операций над нечеткими множествами

Особенности нечетких множеств

Отметим важные особенности теории нечетких множеств.

1) Закон исключенного третьего 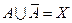и закон контрадикции 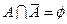, где 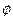- пустое множество верны в классической теории множеств, однако в теории нечетких множеств в общем случае они не выполняются.

Закон исключенного третьего и закон контрадикции в нечеткой теории выглядят следующим образом: 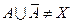и .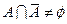

2) В классической теории множеств точка 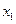из множества A может иметь одну из двух возможностей: 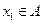or 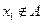. В нечеткой теории точка 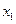может принадлежать множеству A и одновременно не принадлежать A (т.е. принадлежать множеству 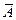) с различными значениями функций принадлежности 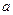и , как показано на рис. 2.7.

Рис. 2.7. Особенность нечетких множеств

Это означает, что в процессе нечетких рассуждений мы можем одновременно рассматривать две возможности, что делает процесс рассуждений более гибким, чем классический.

3) Связь с теорией вероятности. Теория нечётких множеств в определенном смысле сводится к теории случайных множеств и тем самым к теории вероятностей. Описание последовательности теорем, описывающих это сведение, находится вне рамок данной книги [см. ссылки в сайте википедии]. Основная идея состоит в том, что значение функции принадлежности 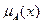можно рассматривать как вероятность накрытия элемента 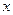некоторым случайным множеством B. Однако при практическом применении аппарат теории нечётких множеств обычно используется самостоятельно, выступая конкурентом к аппарату теории вероятностей и прикладной статистики.