Повторение независимых испытаний. Формула Бернулли
С понятием «независимых событий» связано понятие «независимых испытаний». Испытанием Бернулли называют случайный опыт, который может закончиться одним из двух элементарных событий.
Пример. Подброшенная монета падает либо орлом, либо решкой вверх. Стрелок может попасть в мишень, а может промахнуться.
Вероятность того, что опыт закончится успехом, обычно обозначают р. Неудачи – q. При этом p+q=1.
Если проводится несколько одинаковых и независимых испытаний подряд, то говорят, что проведена серия или последовательность испытаний Бернулли.
Пример.Несколько (n раз) подбрасываний монеты; стрельба (n раз) по мишени; несколько выниманий из урны шара, если шар каждый раз возвращается в урну.
Пример. Рассмотрим элементарные события для последовательности из 3 испытаний стрельбы по мишени. Каждое испытание оканчивается либо событием А – попаданием (успехом), либо событием 
-- промахом (неудачей). Таким образом, после 3 испытаний мы можем получить следующие элементарные события:
, А, А , А , АА , АА, А А, ААА.
Мы получили 8 элементарных событий при трех испытаниях Бернулли. Поскольку отдельные испытания независимы, вероятность каждого элементарного события определяется однозначно. По теореме умножения событие, например, АА имеет вероятность, равную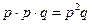 
, событие А -- 
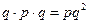и т.д.
Пример.В коробкележат карандаши:3 красных и 5 синих. Таким образом, всего карандашей 8. Вынем наудачу один карандаш. Если А – «карандаш окажется красным», то назовем элементарное событие опыта успехом. Если -- «синий» – неудачей. Такой опыт является испытанием Бернулли. Очевидно, вероятность успеха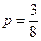 
, неудачи -- 
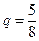. Вынутый карандаш вернем в коробку. Повторим опыт 4 раза. Таким образом получаем серию из 4 испытаний Бернулли. Поставим вопрос: какова вероятность вынуть в первый, третий и четвертый раз красные карандаши, а во второй – синий? Такое событие имеет вид А АА. И вероятность его равна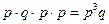 
. Подставив известные значения, получим 
.
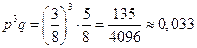Вобщем виде задача, относящаяся к испытаниям Бернулли, состоит в определении вероятности того, что в n независимых испытаниях событие А наступит m раз (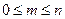 
). Обозначается искомая вероятность 
.
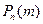Пример. При бросании игральной кости 3 раза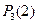 
означает вероятность того, что в 3-х опытах событие А – выпадение цифры 1 – произойдет 2 раза: АА , А А, АА. Тогда получаем,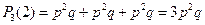 
; 
.
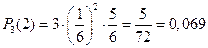Теорема. Если производится n независимых испытаний, в каждом из которых вероятность р наступления события А постоянна, то вероятность того, что событие А произойдет m раз определяется формулой Бернулли
.
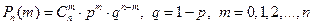Задачи.
- Игрок кидает мяч в баскетбольную корзину. Вероятность попадания равна
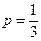. Найти вероятность того, что, сделав 5 бросков, игрок попадет в корзину только при втором и четвертом броске. - Сколько элементарных событий в серии из 8 испытаний Бернулли благоприятствуют:
а) 2 успехам; б) 6 успехам.
3. Проводится серия из 10 испытаний Бернулли. Каких элементарных событий больше: тех, что благоприятствуют 3 успехам, или тех, что благоприятствуют 7 успехам?
4. Проведена серия из n испытаний Бернулли. Найти n, если общее число элементарных событий равно:
а) 16; б) 64; в) 256.
5. Монету подбрасывают 10 раз. Какова вероятность того, что герб выпадет:
а) 4 раза; б) ни разу; в) хотя бы один раз.
6. В семье трое детей. Какова вероятность того, что:
а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки – 0,49.