Естественная форма числа или представление чисел в формате с фиксированной запятой (точкой)

Для представления чисел в этом формате существует следующее правило: запятая располагается в строго определенном месте, отделяющем целую часть от дробной части. Наиболее часто такая форма используется для представления целых чисел. Количество разрядов может быть либо 16 (формат Н), либо 32 (формат F). Во всех форматах знак числа помещается в старший разряд и кодируется как знак 0-для положительного числа, либо как знак 1 –для отрицательного числа.

	Знак	214	213	•••	21	20
Формат Н				•••
				•••
Разряд

	Знак	230	229	•••	21	20
Формат F				•••
				•••
Разряд

Недостатком таких форматов является ограничение величины кодируемого числа. В формате Н можно задать число от -32767₁₀ до +32767, а в формате F от -7FFFFFFF₁₆ до +7 FFFFFFF₁₆.

3.2 Нормальная форма числа или представление чисел в формате сплавающей запятой (точкой).

Для расширения диапазона кодируемых чисел применяется формат с плавающей запятой. Любое число в этом формате представляется в виде

А = ,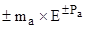

где m_a – мантисса числа А; Е – основание системы счисления; ±Р_а – порядок. Все эти величины двоичные числа без знака.

На рисунке приведен формат числа в нормальной форме:

		2•••7	8•••31
Знак ma	Знак Ра	Ра	ma
Знак ma	Знак Ра	Порядок	Мантисса

Старший разряд содержит знак мантиссы, первый разряд – знак порядка, шесть разрядов (2-7) определяют значение порядка, а остальные величину мантиссы. Нормальная форма может быть представлена коротким форматом Е (4 байта), длинным форматом D (8 байт) и повышенной точности (16 байт). Во всех этих форматах первый байт остается неизменным, а меняется только область, отведенная под мантиссу.

Пример.

В десятичной системе число 15 может быть записано несколькими способами:

Мантисса	Порядок
0,15	102
1,5	101
	10-1

Задача.

Имеется 4-х разрядный регистр данных. Сравнить максимальные числа, которые могут быть записаны в регистр, при естественной и нормальной форме записи.

Решение:

Если под запись числа отводится 4 байта, т.е. 32 бита, то в естественном представлении один бит отводится под знак числа, (32-1) = 31 бит – под целую частью Максимальное число равно:

2³¹ – 1 = 2147483647 ≈2/10⁹

В нормальном представлении один бит отводится под знак мантиссы, один знак – под знак порядка, шесть бит – под значение порядка, (32 – 1 – 1 – 6) = 24 бита – под значение мантиссы. Максимальное число, записанное в мантиссу, есть 0.111…1(24 раза) = 1 – 2^-24≈ 1 – 6*10^-8 ≈ 1

Максимальное число, записанное в порядок (6 бит), есть 2⁶ – 1 = 64 - 1 = 63. Т.е., максимальное число, записанное в нормальной форме, есть

111…1 000…0

, т.е., 2⁶³ – 2³⁹≈⁶³2≈9*10¹⁸

24 раза 63-24=39 раз

Для однозначного представления числа мантиссу нормализуют, т.е. накладывают ограничение 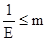<1. Под значение порядка отводится 7 разрядов и один из них знаковый. Следовательно, значение порядка лежит в интервале, т.е. от-64 до 63.

Сместив порядок на 2⁶ = 64 = 40₁₆, получим интервал возможных значений 0 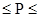2⁷ -1=127. Смещенный порядок на 40₁₆ называется характеристикой и вычисляется как Р_х =Р+40. Если характеристика равна 40, то порядок равен 0; если характеристика меньше 40, то порядок отрицательный; если больше-то положительный.

Задача.

Представить в нормальной форме Е шестнадцатеричный код числа D₁₀ = 32001,5 и D₁₀ = -32001,5.

Так как форма Е – это короткий формат (4 байта), то с использованием шестнадцатеричного кода получим: 32001,5₁₀ = +7D01,8₁₆ и -32001,5₁₀ = -7D01,8₁₆.

Найдем нормализованные мантиссы и характеристики:

m = 0,7D018 <1 Р_х = 40+4 = 44

Знак m	Рх	m
	100 0100	0111 1101 0000 0001 1000 0000

m = -0,7D018 <1 Р_х = 40+4 = 44

Знак m	Рх	m
	100 0100	0111 1101 0000 0001 1000 0000

Машинные коды чисел

В компьютерах все арифметические операции осуществляются в машинных кодах и могут быть сведены к операции сложения и операциям сдвига вправо или влево. Обычно применяются прямой, обратный и дополнительный коды.

Представление чисел в прямом коде осуществляется в виде знакового разряда и абсолютной величины числа.

Задача.

+29₁₀ = 00111101₂ -29₁₀ = 10111101

+127₁₀ = 01111111₂ -127₁₀ = 11111111₂

Для представления отрицательных чисел или замены операции вычитания на сложение используются обратный и дополнительный коды.

Сущность этих кодов заключается в том, что вычитаемое число Х, как отрицательное число, представляется в виде дополнения до некоторой константы С, такого, что С – Х >0. Обратный и дополнительный коды отличаются выбором этой константы.

Для дополнительного кода отрицательное число Z представим как

Z = -Х = (10ⁿ –Х) - 10ⁿ,

где Z <0, Х>0, n – величина разрядной сетки, а 10ⁿ –Х –дополнительный код числа.

Для обратного кода отрицательное число Z представим как

Z = -Х = (10ⁿ – 1 - Х) - 10ⁿ +1,

где Z <0, Х>0, n – величина разрядной сетки, а 10ⁿ – 1 - Х –обратный код числа.

Для положительного числа прямой, обратный и дополнительный коды будут одинаковыми А^п =А^о =А^д.

Задача.

Для числа +31→А^п =А^о =А^д =0000 0000 0001 1111₂.

Для числа -31→ А^п =1000 0000 0001 1111₂.

Для построения дополнительного кода выбираем константу 10¹⁵= 1000 0000 0000 0000 и получаем А^д =1111 1111 1110 0001₂.

Общие правила образования машинных кодов:

-положительное число в прямом, обратном и дополнительном кодах одинаково;

-прямой код отрицательных и положительных чисел имеет различие только в знаковом разряде, модуль числа не меняется;

-обратный код отрицательного числа получается из прямого кода путем инверсии, т.е. замены 1 на 0 и всех 0 на 1, кроме знакового разряда;

-дополнительный код получается из обратного прибавлением 1 к младшему разряду (перенос 1 в знаковый разряд не учитывается);

-дополнительный код отрицательного числа получается из прямого кода заменой всех 1 на 0 и всех 0 на 1, кроме 1 самого младшего разряда и следующих за ней 0.

Обычно в компьютере числа в естественной форме записи хранятся в дополнительном коде, а числа в нормальной форме хранятся в прямом коде. Обратный код применяется для получения дополнительного кода.