Коммутативность дизъюнкции
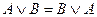
Коммутативность конъюнкции
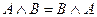
Ассоциативность дизъюнкции
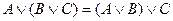
Ассоциативность конъюнкции
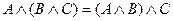
Первый дистрибутивный закон
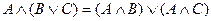
Второй дистрибутивный закон
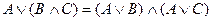
Законы де Моргана
, 
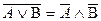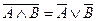
Законы идемпотентности
, 
.
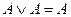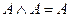10. Законы, включающие тождественно-истинные (I) и тождественно-ложные (L) высказывания
, 
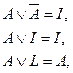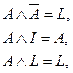
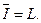
Введенные пять основных логических операций не являются независимыми: одни из них могут быть выражены через другие. В частности, эквиваленция и импликация выражаются через дизъюнкцию, конъюнкцию и отрицание следующим образом:
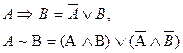
Пример 23.Доказать равносильность
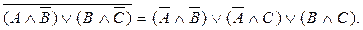
Используя законы де Моргана, можем записать
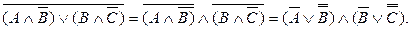
Согласно закону двойного отрицания, получаем
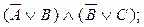
теперь, используя первый дистрибутивный закон, преобразуем полученное выражение далее
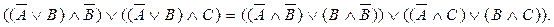
Ассоциативность дизъюнкции позволяет опустить две пары скобок
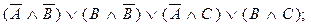
учитывая законы пункта 10: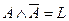 
и 
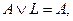окончательно получаем
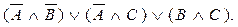
Пример 24.Упростить высказывание
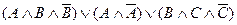
Так как
, , 
,
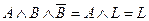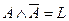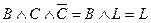то предложенное высказывание равносильно высказыванию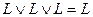 
, т.е. является тождественно-ложным.
Задача 1.
Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники были на синем «Бьюике»; Джонс сказал, что это был черный «Крайслер», а Смит утверждал, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета был автомобиль, и какой марки?
Решение.
Рассмотрим высказывания:
A = {Машина синего цвета},
B = {Машина марки «Бьюик»},
C = {Машина черного цвета},
D = {Машина марки «Крайслер»},
E = {Машина марки «Форд Мустанг»}.
Так как либо цвет машины, либо марка каждым из соучастников преступления названы верно, то
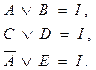
Отсюда следует, что
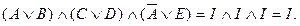
В левой части конъюнкцию трех дизъюнкций можно, используя первый дистрибутивный закон, заменить дизъюнкцией восьми конъюнкций
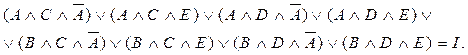
Но
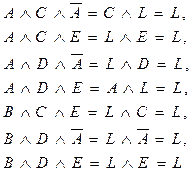
и, следовательно,
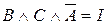, т.е. преступники скрылись на черном «Бьюике».
Задача 2.
На одном заводе работают три друга: слесарь, токарь и плотник. Их фамилии: Борисов, Иванов, Семенов. Профессии и фамилии названы в произвольном порядке. У слесаря нет ни братьев, ни сестер, и он самый младший из друзей. Семенов женат на сестре Борисова, он старше токаря. Назовите фамилии слесаря, токаря и плотника.
Решение.
Составим таблицу, сверху которой для краткости начальными буквами обозначим фамилии друзей и слева – их профессии. В каждую клетку впишем 1, если соответствующая комбинация допустима, или 0, если комбинация противоречит условию задачи.
| Б | И | С | |
| с | |||
| т | |||
| п |
Условия 1 и 3 очевидно исключают возможность того, что Борисов слесарь, поэтому в клетку, стоящую в левом верхнем углу таблицы (клетку (с, Б)), вписываем 0.
Условия 2 и 4 исключают возможность того, что Семенов – слесарь. Поэтому в клетку, стоящую в правом верхнем углу таблицы (клетку (с, С)), также вписываем 0. Но так как один из трех друзей слесарь, то им может быть только Иванов. Поэтому в клетку (с, И) вписываем 1, а в остальные клетки среднего столбца – 0 (если Иванов слесарь, то он не токарь и не плотник).
Условие 4 исключает возможность того, что Семенов токарь. Поэтому в клетку (т, С) вписываем 0, но тогда Семенов может быть только плотником, следовательно, в клетку (п, С) вписываем 1, а в клетку (п, Б) вписываем 0.
Теперь осталась лишь одна незаполненная клетка (т, Б), в которую мы должны, очевидно, вписать 1.
Итак, Борисов – токарь, Иванов – слесарь, Семенов – плотник.
Алгебра логики успешно применяется при анализе релейно-контактных и электронно-ламповых схем. Физическая природа таких схем (будем называть их переключательными) может быть самой разнообразной. Под переключательной системой будем понимать схематическое изображение какого-либо устройства, содержащего только двухпозиционные переключатели, т.е. переключатели, которые могут находиться только в двух состояниях: в замкнутом (ток проходит) и в разомкнутом (ток не проходит). Связь между переключательными схемами и алгеброй высказываний устанавливается следующим образом. Каждому переключателю ставится в соответствие высказывание, истинное тогда, когда переключатель замкнут, и ложное, если переключатель разомкнут. На схемах переключатели будем обозначать теми же буквами, что и соответствующие им высказывания.
Переключателям, соединенным параллельно, будет соответствовать при этом дизъюнкция соответствующих высказываний; переключателям, соединенным последовательно, − конъюнкция высказываний. Если два переключателя работают так, что один из них замкнут, когда другой разомкнут, и наоборот, то им ставятся в соответствие высказывания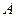 
и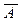 
.
Каждой переключательной схеме, таким образом, будет поставлено в соответствие сложное высказывание, истинное тогда и только тогда, когда схема проводит ток. Это сложное высказывание можно исследовать методами математической логики. Если такое сложное высказывание удается упростить, то соответствующая схема допускает аналогичное упрощение. Естественно считать из двух схем более простой ту, которая содержит меньше переключателей.
Пример 25.Упростить схему:
 |
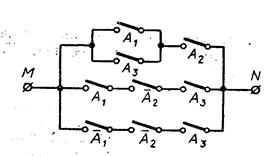Выписываем высказывание, соответствующее данной схеме, и упрощаем его:
=
= 
=
= 
=
= 
= 
.
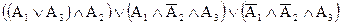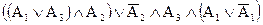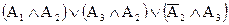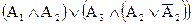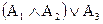Следовательно, рассматриваемая схема может быть заменена более простой, содержащей только три переключателя. Исходная схема содержала 9 переключателей.
Построим упрощенную схему по аналогии с предыдущей:
 |
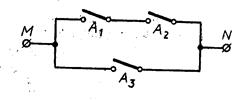1.5. Содержание отчета:
1. Выполнение заданий соответствующего варианта.
2. Ответы на контрольные вопросы.
1.6. Контрольные вопросы:
1. Что такое система счисления?
2. Чем отличаются позиционная и непозиционная системы счисления?
3. Почему основной системой счисления ЭВМ является двоичная?
4. Когда используется шестнадцатеричная система счисления?
5. Какие основные операции алгебры логики вы знаете?
6. Как можно проверить эквивалентность формул в алгебре высказываний?