Закодируйте сообщениеα кодом Хемминга из задачи 4.4.4

а) α =(0011)	б) α =(1011)	в) α =(0111)	г) α =(0001)	д) α =(0010)
е) α =(1010)	ж) α =(0110)	з) α =(1001)	и) α =(1000)	к) α =(1100)

Образец:Закодируйте сообщениеα=(0101)кодом Хемминга из задачи 4.4.4. (образец):

Решение: Умножим кодовое слово a на порождающую матрицу G:

.

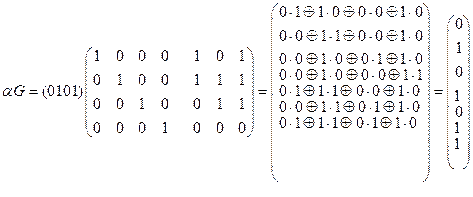Отсюда кодированное сообщение имеет вид (0101011).

Первые m=4 информационные символы вектора αG образуют исходное сообщение α=(0101), последние n-m=3символа используются для контроля.

4.4.6. Решите задачу:

Декодируйте кодом Хемминга сообщение b в задаче 4.4.3.:

а) b =(1100110)	б) b =(1010111)	в) b =(1111110)	г) b =(0100011)	д) b =(1101101)
е) b =(1110110)	ж) b =(1001101)	з) b =(0010010)	и) b =(1110111)	к) b =(1010001)

Образец: Декодируйте кодом Хемминга сообщение b=(0111001) в задаче 4.4.3.

Решение: Умножим проверочную матрицу 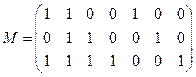из задачи 4.30 на вектор-столбец 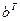= 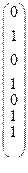– транспонированное сообщение b. Имеем

.

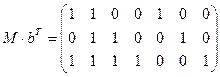
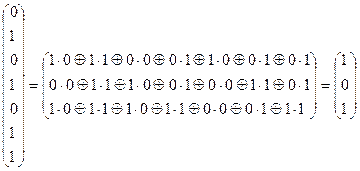Т.к. в результате получен ненулевой вектор 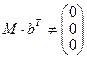, то это означает, что при декодировании была допущена ошибка. Т.к. этот вектор-столбец 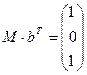совпадает с первым столбцом проверочной матрицы M, то надо изменить, (инвертировать) именно первый символ в сообщении b. Получим новый вектор b_н=(1111001), в котором при m=4 первые четыре буквы a=(1111) составляют истинное декодированное сообщение.

4.4.7.Построить коды H(b) для заданных слов b=(010101), x=(110100), y=(011010).

Решение.

1) Для построения кодов H(b) необходимо иметь двоичные векторы, записанные словом длиной k. Рассчитаем по k формуле 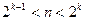. При n = 6 имеем неравенство 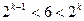. Отсюда т.к. 4<6<8, то 2²<6<2³. Значит k=3.

2) Двоичные векторы длины 3 обозначим e₃:

n
e3(n)	e3(1)	e3(2)	e3(3)	e3(4)	e3(5)	e3(6)
Код

2) Т.к. число b=(010101) содержит знаки 1 в четных разрядах, то для записи H(b) в векторной форме нам понадобятся только те векторы e₃, которые имеют четные номера. Отсюда имеем

H(b)= (0,1,0) Å (1,0,0) Å (1,1,0)=(0,0,0).

Для слова x=(110100) значащие разряды первый, второй и четвертый, поэтому

H(x)= (0,0,1) Å (0,1,0) Å (1,1,0)=(1,1,1).

Для слова y=(011010) значащие разряды второй, третий и пятый, поэтому

H(y)= (0,1,0) Å (0,1,1) Å (1,0,1)=(1,1,0).

Согласно теореме, bÎ H6, .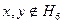

4.4.8. Решите задачу. В двоичном слове b в задаче 4.4.6. произошла замена одного из символов. С помощью векторной формы кода Хемминга найдите и исправьте ошибку.

Образец: Пусть в слове b=(110101) произошла замена одного из символов, например, первого. Новое слово А=(110101). Докажите с помощью векторной формы кода Хемминга, что заменен именно первый символ.

Решение: Найдем H(A)=(0,0,1) Å (0,1,0) Å (1,0,0) Å (1,1,0)=(0,0,1), что соответствует числу 1. Т.к. Полученный кортеж (001) есть двоичная форма числа 1, то первый разряд есть номер замещенного места.

4.4.9. Решите задачу:

Закодируйте слово длины 4 с помощью кода с проверкой четности.

а) α=(0011)	б) α=(1011)	в) α=(0111)	г) α=(0001)	д) α=(0010)
е) α=(1010)	ж) α=(0110)	з) α=(1001)	и) α=(1000)	к) α=(1100)

Образец: Закодируйте слово α=(0101) длины 4 с помощью кода с проверкой четности.

Решение: Найдем сумму по модулю 2 всех двоичных букв этого слова. Имеем:

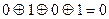, поэтому передано будет сообщение в виде слова b=(01010) длины 5.

4.4.10. Решите задачу:

Декодируйте слово длины 5 с помощью кода с проверкой четности

а) b=(00110)	б) b=(10111)	в) b=(01110)	г) b=(00011)	д) b=(00101)
е) b=(10100)	ж) b=(01100)	з) b=(10010)	и) b=(10001)	к) b=(11001)

Образец: Декодируйте слово b=(01110) длины 5 с помощью кода с проверкой четности.

Решение: Отбросив последнюю букву передаваемого слова, имеем слово α=(0101) длины 4, которое передавалось по каналу связи (в задании 4.4.9).

4.4.11. Решите задачу:

Определите, допущены ли ошибки в сообщении, заданном в задании 4.4.10.

Образец: Определите, допущены ли ошибки в сообщениях a₁=(01110) и a₂= (01010).

Решение: Для обнаружения ошибки, проверим с помощью М2 сумму всех букв закодированного слова в полученных сообщениях: a₁= 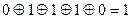. Т.к. сумма всех букв закодированного слова оказалась равной 1, то при его передаче по каналу связи была допущена ошибка.

Для второго сообщения имеем a₁= 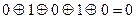. Т.к. сумма всех букв закодированного слова оказалась равной 0, то при его передаче по каналу связи код с проверкой четности не позволяет выявить ошибку.

4.4.12. Для заданного сообщения А построить код Хемминга B. Необходимо обнаружить и справить одиночную ошибку, если при хранении информации она приобрела вид:

а) 1011010	б) 1001000	в) 1011100	г) 0011000	д) 1010000
е) 1111000	ж) 1011001	з) 10110000	и) 010110	к) 101010

Образец: Для заданного сообщения A=101100 построить код Хемминга B.

Решение:Кодируемое словоA=101100 длины m=6.

1) Рассчитаем k по формуле 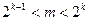. При m = 6 имеем неравенство 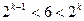. Отсюда т.к. 4<6<8, то 2²<6<2³. Значит k=3 и закодированное слово должно быть длиной m+ k =6+3=9. Значит, код содержит 6 информационных и 3 проверочных символа, расположенных на местах, соответствующих разрядам, равным целым степеням числа 2. Тогда проверочные символы расположены на 2^k местах: т.е. занимать 2⁰=1, 2¹=2, 2²=4, разряды. Остальные разряды двоичного числа заняты информационными символами.

2) Обозначим через p_i символы, расположенные на проверочных i–ых разрядах. Тогда код В должен иметь вид двоичного числа, в котором на 1-м, 2-м и 4-м месте расположены проверочные символы p_1, p₂, p₄, а на остальных местах разместим информационные символы, взятые из заданного числа A=101100. Тогда код В примет вид:

p₁ p₂1 p₄01100

3) Для вычисления проверочных символов составим таблицу:

i	i в двоичном представлении	Информац. позиции	Расчет проверочных символов	Провероч. позиции	Сообщение после кодирования	Номер строк, формирующих провер.символ
	0001		p3Å p7			3 и 7
			p3Å p6Å p7			3, 6 и 7
	0011
			p6Å p7			6 и 7
	0110
	0111

Для вычисления проверочных символов будем учитывать, что p_i равно сумме по модулю 2 тех информационных символов, номера которых имеют единицу в двоичном представлении в i–ых разрядах, считая справа налево: p₁ – в первом разряде справа, p₂ – во втором разряде, p₄ – в третьем разряде справа. Т.к. информационные позиции для единиц в первом разряде, расположенных на 3-м и 7-м местах, то p₁ = p₃Å p₇=1 Å 1=0.

Т.к. информационные позиции для единиц во втором разряде, расположены на 3-м , 6-м и 7-м местах, то p₂ = p₃Å p₆Å p₇=1 Å 1Å 1=1.

Т.к. информационные позиции для единиц в третьем разряде справа расположены на 6-м и 7-м местах, то p₄ = p₆Å p₇=1Å 1=0.

4) Объединим информационные и проверочные символы. Тогда закодированное кодом Хемминга сообщение имеет вид: В=011001100.

5) Проверим правильность построенного кода. Для этого найдем значение H(B). Для этого выпишем столбец, составив его из двоичных номеров строк, в которых знак кода В равен 1, т.е. 2-ю,3-ю,6-ю и 7-ю строки. Если сумма М2 номеров в каждом разряде равна 0, то код составлен без ошибок:

Номер строки	Двоичное представление номера строки	Знак сообщения В
	0011
	0110
	0111
Сумма разрядов М2

Действительно, в каждом из разрядов получен ноль, значит код составлен верно.

4.4.13. В построенный в задании 4.4.12. код Хемминга внести одиночную ошибку. Необходимо обнаружить и справить эту одиночную ошибку в коде Хемминга B.

Образец. В образце задания 4.4.12. сообщение, закодированное кодом Хемминга, имеет вид: В=011001100. Пусть при передаче сообщения произошла замена символа в пятом разряде. Необходимо обнаружить и справить эту одиночную ошибку в коде Хемминга B.

Решение. Новое сообщение имеет вид В*=011011100.

1) Для обнаружения ошибки, найдем значение H(B*). Для этого выпишем в столбец двоичные номера строк, в которых знак сообщения В* равен 1. Найдем сумму М2 знаков номеров в каждом из разрядов.

i	Двоичное представление номера строки	Сообщение после его передачи
	0001

i	Двоичное представление номера строки	Сообщение после его передачи

Полученное число 0101 есть двоичная форма десятичного числа 5: 0101₂=5₁₀. Это означает, что именно в пятом разряде сообщения В*=011011100 произошла замена символа. Чтобы исправить ошибку, заменим символ 1 в пятом разряде на символ 0. Действительно, сообщение имело вид: В=011001100.