Электрический диполь и его поле

В. Г. Лещенко

ЭЛЕКТРИЧЕСКИЕ ПОЛЯ БИОТКАНЕЙ И МЕТОДЫ ИХ РЕГИСТРАЦИИ

Учебно-методическое пособие

Минск 2007

УДК 612.014.421 (075.8)

ББК 28.707.1 я 73

Л 54

Утверждено Научно-методическим советом университета в качестве
учебно-методического пособия 29.11.2006 г., протокол № 3

Рецензенты: зав. каф. гистологии, цитологии и эмбриологии Белорусского государственного медицинского университета, проф. Б. А. Слука; ст. науч. сотр. Белорусского национального технического университета, доц. Г. И. Олефир

Лещенко, В. Г.

Л 54 Электрические поля биотканей и методы их регистрации : учеб.-метод. пособие / В. Г. Лещенко. – Минск: БГМУ. 2007. – 19 с.

ISBN 978–985–462–678–9.

Рассматриваются основные характеристики электрических полей, образующихся точечными зарядами и простейшей электронейтральной системой — диполем, а также методы описания и регистрации электрических полей, создаваемых органами и тканями человека. Достаточно подробно рассмотрено формирование электрокардиограммы и способы ее регистрации.

Предназначено для студентов всех факультетов.

УДК 612.014.421 (075.8)

ББК 28.707.1 я 73

ISBN 978–985–462–678–9 © Оформление. Белорусский государственный

медицинский университет, 2007

1. Электрическое поле и его основные характеристики

Все тела в природе состоят из атомов, которые, в свою очередь, состоят из положительно заряженных ядер и отрицательно заряженных электронов. Именно электростатические силы притяжения удерживают атомы и молекулы в устойчивом состоянии. Электрические взаимодействия определяют физическое и химическое строение атомов и молекул, свойства твердых тел, газов, жидкостей и биологических структур. Знание законов взаимодействия электрических зарядов между собой и с внешними электрическими полями необходимо для понимания процессов формирования электрических полей органов и тканей, методов регистрации и механизмов воздействия внешних электрических полей на биологические объекты.

В природе известны два вида электрических зарядов, которые были условно названы положительными и отрицательными. В международной системе (СИ) единицей электрического заряда является 1 Кулон (Кл) — это заряд, который проходит за 1 секунду через поперечное сечение проводника при токе в 1 Ампер (А): 1 Кл = 1А·1 с. Наименьшим элементарным отрицательным зарядом обладает электрон, а таким же по величине, но положительным — протон. Величина элементарного заряда равна
е = 1,6·10^–19 Кл.

Одним из важнейших законов природы является закон сохранения электрического заряда: в замкнутой системе тел алгебраическая сумма электрических зарядов всегда остается постоянной при любых взаимодействиях этих тел между собой.

Опыт показывает, что заряды одного знака всегда отталкиваются, а разных — притягиваются. Сила взаимодействия между точечными зарядами q₁ и q₂, расположенных на расстоянии r друг от друга, определяется законом Кулона:

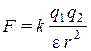, (1.1)

где 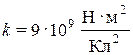— постоянная электрического взаимодействия; а ε — относительная диэлектрическая проницаемость среды, в которой находятся заряды.

Способность электрических зарядов взаимодействовать на расстоянии объясняется тем, что каждый из них создает вокруг себя электрическое поле, которое оказывает силовое воздействие на любой внесенный в него другой заряд. Поэтому, чтобы определить наличие электрического поля в какой-либо точке среды, в нее помещают пробный заряд q₁. 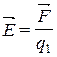Сила F действия поля на этот заряд будет пропорциональна величине внесенного заряда q₁, где отношение не зависит от величины пробного заряда, а является силовой характеристикой электрического поля, которую называют напряженностью 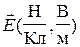. Если напряженность 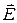поля известна, то сила, действующая на любой заряд q₁, внесенный в это поле, равна

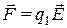. (1.2)

Как видно из (1.1), закон Кулона применим только для точечных зарядов и шаров, а формула (1.2) — для любых зарядов и полей. Из векторного равенства (1.2) следует, что сила, действующая на положительный заряд, имеет такое же направление, как и вектор 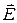напряженности поля, а сила, действующая на отрицательный заряд, — противоположное ему.

Электрические поля принято изображать силовыми линиями. Это направленные линии, касательные к которым совпадают с направлением вектора напряженности 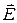поля в этой точке. Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным, т. е. начинаются на положительных зарядах и заканчиваются на отрицательных. Электрическое поле называют однородным, если его напряженность одинакова по величине и направлению во всех точках пространства: 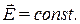Такие поля изображаются параллельными равноотстоящими друг от друга силовыми линиями.

Напряженность поля, создаваемого точечным зарядом q₀, находят, пользуясь законом Кулона, по следующей формуле:

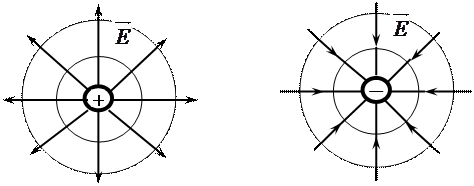
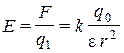. (1.3)

Эта формула справедлива и для поля, создаваемого заряженным шаром радиуса R в окружающем его пространстве, т. е. при r ≥ R. Такое поле неоднородно, так как различно по величине и по направлению в разных точках пространства. На рисунке 1 стрелками показаны силовые линии электрических полей, создаваемых положительным и отрицательным точечными зарядами, а концентрическими окружностями — линии равного потенциала.

Рис. 1. Силовые и эквипотенциальные линии электрических полей точечных зарядов

Если электрическое поле создается не одним зарядом, а несколькими, то для определения напряженности результирующего поля следует применить принцип суперпозиции полей: напряженность электрического поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке среды каждым из зарядов:

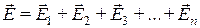. (1.4)

Поскольку на заряд q, помещенный в электрическое поле, действует сила F = qE, то он может переместиться вдоль силовой линии на расстояние S и совершить работу А = FS = qES. Это означает, что любой заряд q, находящийся в электрическом поле, обладает потенциальной энергией
W_пот = А, которая пропорциональна величине этого заряда q. Но отношение j 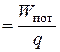уже не зависит от величины заряда, а является энергетической характеристикой поля, называемой его электрическим потенциалом φ. Единицей потенциала в СИ является 1 Вольт: 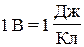. Совокупность всех точек поля, имеющих одинаковый электрический потенциал, образует эквипотенциальную поверхность, которая всегда перпендикулярна линиям напряженности поля.

Потенциал электрического поля, создаваемого точечным зарядом q₀, определяется формулой:

j 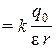. (1.5)

В этом случае поверхностями равного потенциала являются сферы радиуса r, тогда как силовые линии, идущие из центра сферы по радиусам, перпендикулярны этим сферам (рис. 1).

Если электрическое поле создает не один заряд, а система зарядов, то потенциалэлектрического поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых в данной точке среды каждым из зарядов:

φ = φ₁ + φ₂ + φ₃ + … + φ_n. (1.6)

Очевидно, что определение потенциала сложного поля значительно проще, чем вычисление его напряженности, требующей нахождения векторной суммы.

Если электрическое поле перемещает заряд q из одной точки поля в другую, то оно совершает работу А (Дж):

А = W_пот1 – W_пот2 = q (φ₁ – φ₂) = qU. (1.7)

Величина U = φ₁ – φ₂ называется разностью потенциалов или напряжением между двумя точками поля и тоже измеряется в вольтах.

Следует обратить внимание на очень важное свойство электрического поля: работа в электрическом поле не зависит от траектории перемещения заряда из т. 1 в т. 2, а определяется только разностью потенциалов между ними.

Из формулы (1.7) следует также, что при перемещении заряда по
эквипотенциальной поверхности работа не совершается, т. к. φ₁ = φ₂ и
А = U = 0.

В общем случае напряженность Е электрического поляравна градиенту потенциала с обратным знаком:

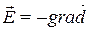j, (1.8)

поэтому, зная распределение потенциала φ(r) в пространстве,можно найти распределение напряженности поля Е(r) и наоборот. Знак «–» указывает, что вектор напряженности направлен против градиента потенциала, т. е. в сторону наибыстрейшего уменьшения потенциала. Для однородного поля, силовые линии которого параллельны оси Ох, соотношение (1.8) принимает вид:

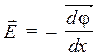. (1.9)

Значения напряженности и потенциала электрического поля, создаваемого точечным или сферическим зарядом q₀, определяются формулами (1.3) и (1.5).

Таким образом, электрически заряженная система тел всегда создает вокруг себя электрическое поле. Но оказывается, что электрически нейтральная система зарядов тоже может создавать вокруг себя электрическое поле. Простейшей такой системой является электрический диполь.

Электрический диполь и его поле

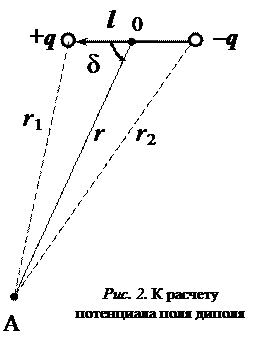
Электрический диполь представляет собой электрически нейтральную систему, состоящую из двух равных по величине, но противоположных по знаку точечных зарядов (+q) и (–q), расположенных на некотором расстоянии l друг от друга. Хотя такая система электрически нейтральна, она создает вокруг себя электрическое поле.

Рассчитаем потенциал этого поля в произвольной точке А, расположенной на расстояниях r₁ и r₂ от положительного и отрицательного зарядов диполя (рис. 2). Суммарный потенциал в т. А равен:

j_А = j₊ + j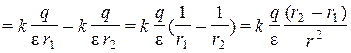_– , (2.1)

где произведена замена r₁ · r₂ ≈ r². Учитывая, что (r₂ – r₁) ≈ l cos δ, получим:

j_А 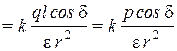. (2.2)

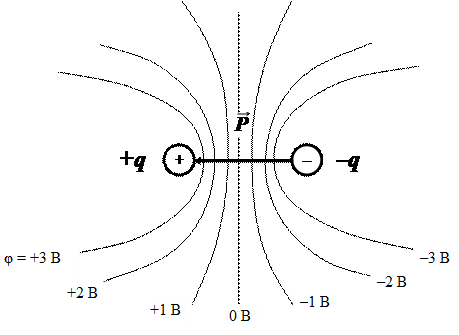
Видно, что потенциал φ поля прямо пропорционален величине р = ql,которая называется дипольным моментом и является важнейшей электрической характеристикой диполя. Дипольный момент 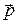— это вектор, направленный вдоль оси диполя от (–q) к (+q). Зная этот вектор, можно вычислить потенциал в любой точке поля, пользуясь формулой (2.2). Из (2.2) в частности следует, что в плоскости, проходящей через середину диполя перпендикулярно его оси (δ = 90^о), потенциал равен нулю, положителен со стороны положительного заряда и отрицателен со стороны отрицательного заряда. Примерное распределение эквипотенциальных поверхностей поля диполя приведено на рисунке 3.

Рис. 3. Линии равного потенциала электрического поля диполя

Таким образом, зная дипольный момент, можно вычислить потенциал поля диполя в любой точке пространства, пользуясь соотношением (2.2). Но на практике, в частности в электрографии, часто приходится решать обратную задачу: необходимо определить величину и направление электрического момента диполя, измеряя разность потенциалов (напряжение) между разными точками А и В создаваемого им поля.

Найдем связь дипольного момента 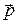и напряженияU_АВ = φ_А – φ_Вмежду двумя равноудаленными от центра диполя точками А и В (r_A = r_B = r) (рис. 4).

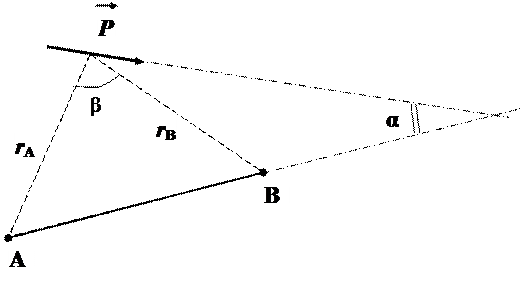Рис. 4. К определению связи между дипольным моментом 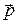и напряжениемU_АВ

Расчет, который здесь не приводится, дает следующее выражение для вычисления напряжения между этими точками:

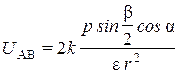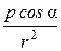~ . (2.3)

Из (2.3) видно, что разность потенциалов между точками А и В прямо пропорциональна проекции вектора дипольного момента на линию АВ, соединяющую эти точки. Необходимо учитывать, что с удалением от диполя напряжение убывает как 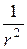, т. е. обратно пропорционально квадрату расстояния от диполя. Поэтому, чтобы полностью определить величину и направление вектора 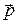, надо знать как минимум две его проекции на разные направления АВ и ВС, при этом точки регистрации потенциалов А, В и С должны быть равноудалены от центра диполя (r_A = r_B = r_C), а отрезки АВ и ВС должны быть видны из центра диполя под одинаковыми углами β. В связи с этим наиболее удобным способом выбора точек регистрации потенциала являются вершины правильного многоугольника, в центре которого находится диполь 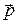. В простейшем случае это будут вершины равностороннего треугольника.

Отметим, что диполь — простейшая, но не единственная нейтральная система зарядов, создающая вокруг себя электрическое поле (рис. 5).

К простым электронейтральным системам относятся также квадруполь (2 положительных и 2 отрицательных равных по модулю заряда), октуполь (4 положительных и 4 отрицательных заряда) и др., которые называют одним словом мультиполи.

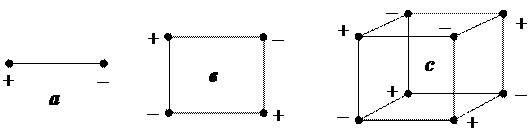Рис. 5. Электрически нейтральные мультиполи:

а — диполь; в — квадруполь; с — октуполь

Потенциалы полей, создаваемых ими, быстро убывают с расстоянием. Так, если потенциал поля точечного заряда убывает с расстоянием как 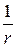, то потенциал поля диполя — как 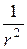, квадруполя — как 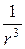, октуполя — как 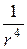и т. д.

Электрическое поле создают не только указанные простейшие мультиполи, но и более сложные электрически нейтральные системы, в том числе биологические ткани и органы.

Из математической физики известно, что любое стационарное электрическое поле, сформированное электрически нейтральной системой зарядов, можно приближенно представить как сумму электрических полей, создаваемых диполем, квадруполем, октуполем и т. д. Наибольший вклад в это суммарное поле, как правило, вносит диполь, поэтому обычно ограничиваются рассмотрением только дипольной составляющей сложного поля, что во многих случаях оказывается полностью оправданным.

Электростатический диполь хорошо описывает электрическое поле в непроводящих средах, т. е. в диэлектриках, где нет свободных зарядов и поэтому нет и токов проводимости. Однако многие биоткани — кровь, лимфа, спинномозговая жидкость, мышцы, нервная ткань, и др. — являются хорошими проводниками, и в них под действием электрических полей возникают электрические токи.

В этих условиях электрическое поле, создаваемое биотканями, более правильно рассматривать не как поле электростатического диполя, а как поле, образованное токовым диполем. Такое представление в электрокардиографии впервые было развито еще Гельмгольцем, а затем подробно рассмотрено другими исследователями.

Токовый диполь 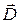представляет собой вектор, равный произведению полного тока 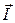на расстояние d между его истоком и стоком.

Исток и сток тока равной интенсивности i, отстоящие друг от друга на небольшое расстояние d, образуют диполь тока с моментом id. Большое число таких малых диполей, расположенных рядом и ориентированных в одном и том же направлении, образует двойной слой, на одной стороне которого размещены истоки, а на другой — стоки. Общий дипольный момент такого двойного слоя равен векторной сумме моментов составляющих его токовых диполей. Каждый малый диполь, как и любой вектор, можно разложить на три взаимно перпендикулярных компонента. Соответствующие компоненты всех диполей можно сложить и в результате будут получены три суммарных компонента одного эквивалентного токового диполя .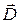

Сопротивление двойного слоя толщиной d и площадью поперечного сечения S равно: R = r 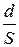, (2.4)

где r — удельное сопротивление среды, Ом·м.

Если истоки, расположенные на одной стороне этого слоя, генерируют ток величиной I (Ампер), создавая дипольный момент D = I · d, то между поверхностями двойного слоя в результате прохождения этого тока возникает разность потенциалов:

U = IR= 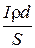= 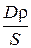, (2.5)

Гельмгольц показал, что потенциал φ, создаваемый таким двойным слоем в любой точке А бесконечной однородной изотропной среды с чисто омическим сопротивлением, равен произведению телесного угла W, под которым видна положительная сторона этого слоя (истоки) из точки измерения, на разность потенциалов, создаваемой токовым генератором (диполем) между сторонами этого слоя, т. е.

φ_А = UW, (2.6)

Поскольку 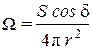, где δ — угол между нормалью к поверхности S (т. е. направлением тока I или диполя D) и направлением на точку наблюдения А, то с учетом (2.5) потенциал в т. А можно представить в виде:

j_А 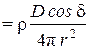~ 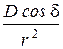. (2.7)

Это выражение полностью аналогично выражению (2.2) для потенциала поля электростатического диполя. Поэтому, с математической точки зрения, выражения для потенциалов электрических полей, создаваемых электростатическим диполем и токовым диполем, аналогичны и формулу (2.3), связывающую разность потенциалов между двумя точками поля А и В и дипольным моментом D, можно получить и в случае токового диполя:

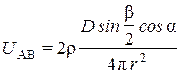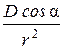~ . (2.8)

Как и в случае электростатического дипольного момента 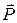, для определения величины и направления вектора токового дипольного момента 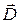точки регистрации потенциалов лучше выбирать в вершинах правильного многоугольника, в центре которого находится диполь; в простейшем случае это будут вершины равностороннего треугольника.