Вычисление расширенной неопределенности оценки значения величины Y

При однократных измерениях неопределенности типа А отсутствуют. Стандартную неопределенность типа В вычисляют по формуле

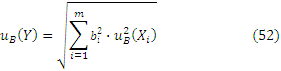
а расширенную по формуле (26).

В случае многократных измерений вычисляют также стандартную неопределенность типа А

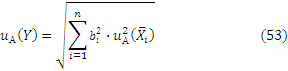
Формулы (52) и (53) отличаются числом слагаемых.

Раздельное вычисление стандартных неопределенностей типа А и типа В обусловлено с одной стороны разной степенью корреляции между оценками неопределенностей, относимых к типу А и к типу В. С другой стороны по соотношению оценок неопределенностей разных типов можно сделать выводы о целесообразности многократных измерений, об ограничении числа наблюдений, о выборе пути по повышению точности результата измерений.

Расширенная неопределенность величины Y

Коэффициент охвата k_o выбирают по правилам, изложенным в разделе (3.6 ).

Эффективное число степеней свободы вычисляют по формуле

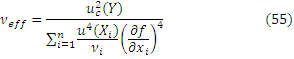
где ν_i – число степеней свободы при определении оценки i –ой входной величины:

ν_i = m_i – 1 - если u (X_i) есть неопределенность типа А и

ν_i = ∞ - если u (X_i) есть неопределенность типа В.

Возможным вариантом нахождения величины Y при многократных измерениях аргументов является вычисление оценок значений Y_k для каждой совокупности одновременно наблюдаемых отсчетов X_ik . После чего для ряда значений Y_k (k =1…m) определяют вероятностные характеристики и результат измерения по правилам, изложенным в разделе 3.6. Этому методу, называемому методом приведения, отдают предпочтение, если зависимость (31) нелинейная.

Простейшими математическими действиями с результатами измерений являются сложение и вычитание. Они, например, присутствуют при определении значения блока мер; при реализации метода сравнения с мерой или другой величиной, значение которой известно; при взвешивании вещества в таре; при исключении из показания омметра сопротивления соединяющих проводов и т.д.

Оценка значения искомой величины равна алгебраической сумме оценок измеряемых величин

,

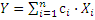где с_i =+1 для слагаемых и -1 – для вычитаемых аргументов.

Суммарная дисперсия определится как

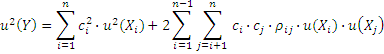
или

В зависимости от значений коэффициентов с_i поправка на корреляцию (вторая сумма в правой части формулы) может быть со знаком плюс или со знаком минус. В первом случае оценка суммарной неопределенности увеличивается, во втором уменьшается. Если значение ρ_ij достаточно близко к единице [25] пренебрежение корреляцией может внести существенную ошибку в оценку неопределенности результата измерения.

Пример 17. Оценить погрешность измерения размера детали в интервале от 50 до 80 мм многооборотной измерительной головкой 2МИГ, устанавливаемой на штативе и настраиваемой с помощью плоскопараллельных концевых мер длины 4 класса точности.

Решение. Исходя из требования, что число плиток в блоке не должно превышать 5 штук, предполагаем, что блок будет состоять из одной плитки 40,50,60 или 70 мм и не более четырех из интервала до 10 мм. Пределы погрешности плиток, определяемые классом точности Δ _40-70 = 4 мкм и Δ _{до 10} = 2 мкм.

Предел допустимой погрешности прибора 2 МИГ : Δ _МИГ = 5 мкм.

Погрешности плиток и прибора заданы предельными значениями. Для них принимаем распределение по закону равной вероятности. Стандартные неопределенности оцениваются по типу В. Тогда получим:

u_B.40-70= Δ _40-70 /√3=4/1,73=2,31мкм, u_B.0-10=2/√3=1,15 мкм, u_B.МИГ=5/√3=2,89 мкм.

Неопределенности типа А отсутствуют. Найдем суммарную стандартную неопределенность, мкм

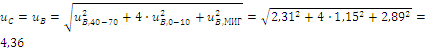
Вычисляем расширенную неопределенность в предположении нормального закона распределения. При вероятности 0,95 принимаем коэффициент охвата, равным 2. Получим

U= k_o∙u_C = 2∙4.36=8,72 мкм.

С учетом рекомендаций по представлению результатов измерений (см. раздел 3.9) запишем U=9 мкм.

Пример 18 [21].Силу электрического тока определяют на основе прямых измерений напряжения с помощью вольтметра и токового шунта

Уравнение измерений

I = f(V,R)=V/R ,

где I - сила тока, V - напряжение, R - сопротивление шунта.

В результате измерений напряжения при температуре t=(23.00±0,05)⁰C получен ряд оценок значений V_i , мВ ( i= 1, …, n; n= 10): 100,68; 100,83; 100,79; 100,64; 100,63; 100,94; 100,60; 100,68; 100,76; 100,65.

Вычисляем среднее арифметическое значение напряжения

Значение сопротивления шунта установлено при его калибровке для I=10А и t=23⁰C и равно: R₀=10,088 Oм

Находим оценку значения силы тока

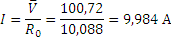
На основе ряда наблюдений значения напряжения определяем стандартную неопределенность по типу А, мВ

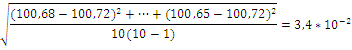
Стандартную неопределенность силы тока определяем по формуле (53)

Находим стандартные неопределенности, относимые к типу В. Принимаем равномерный закон распределения.

1. Согласно результатам калибровки погрешность вольтметра зависит от его показания Δ=±3∙10^-4∙V+0,02 . Тогда стандартная неопределенность u_B,V будет равна

2. Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны ±7∙10^-4∙R. Тогда при R=R ₀ найдем

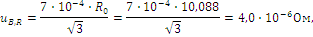
3. Границы неопределенности значения сопротивления шунта, обусловленного изменением температуры, равны ± α·Δt· R₀ . Где

α=6∙10^-6К^-1 – температурный коэффициент. При Δt =± 0,05⁰С границы неопределенности значения сопротивления равны

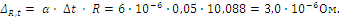
Стандартная неопределенность

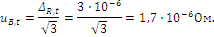
Стандартная неопределенность u_B,I в соответствии с формулой (52)

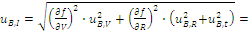
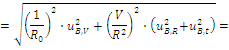
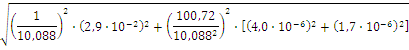
Вычисляем суммарную стандартную неопределенность

Для определения эффективного числа степеней свободы υ_eff используем формулу (55)

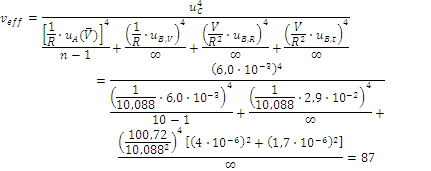
При полученном числе степеней свободы и доверительной вероятности 0,95 коэффициент охвата k равен (таблица 8)

k=t_P(υ_eff)=t_0,95(87)=1,99

Расширенная неопределенность

U_0,95(I)= k_o · u_C(I) = 1,99·6,0·10^-3 = 0,012 A

Запишем результат измерения: I = 9,984 А, U=0,012 А, k_o = 2, Р=0,95.

Вычисление характеристик погрешности результата измерений.

Для сравнения и ознакомления с реализацией на практике ниже приведено решение рассмотренной задачи в терминах погрешности измерений

Вычисляем СКО, характеризующие случайную составляющую погрешности при измерениях напряжения , мВ

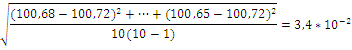
Границы неисключенной систематической погрешности вольтметра определены при его калибровке в виде следующего выражения (в выражениях для границ погрешностей при разных значениях отклонений от нуля будем опускать знак ±):

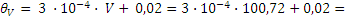
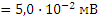
Границы неисключенной систематической относительной погрешности значения сопротивления шунта, определенные при его калибровке, равны δ _R=0,07%. Значение абсолютной погрешности

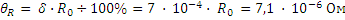
Погрешность измерения температуры равна Δt =± 0,05⁰С. Находим связанные с ней границы неисключенной систематической составляющей погрешности значения сопротивления шунта

Предполагаем равномерный закон распределения неисключенных систематических составляющих погрешности результата измерений. Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока будет равно

После подстановки получим

Найдем границы суммарной неисключенной систематической составляющей погрешности результата измерений силы тока при доверительной вероятности Р = 0,95

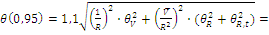
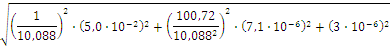
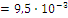А.

СКО случайной составляющей погрешности результата измерений силы тока S равно

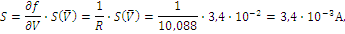
Вычислим СКО суммарной погрешности результата измерений силы тока

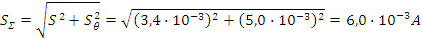
Доверительные границы погрешности результата измерений силы тока при Р = 0,95 и эффективном числе степеней свободы

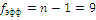
Результат измерения I = (9,984±0,012) А, Р=0,95.

В некоторых случаях для характеристики результата косвенного измерения используют максимально гарантированное значение погрешности - так называемый предел погрешности

где Δ (X_i) - предел погрешности измеренного значения величины X_i.

Пример 19. Выбрать более точный способ получения значения сопротивления электрической цепи (прямое или косвенное измерение) с помощью измерительных приборов.

Омметр R_max = 150 Омкласс точности 1,5

Вольтметр U_max = 300 Bкласс точности 2,0

Амперметр I_max = 25 Aкласс точности 2,5.

Числовые значения характеризуют наибольшее значение величины на шкале прибора.

Параметры электрической цепи U=180 В, I=10 А, R=18 Ом.

Находим предел погрешности омметра

Δ_R =1,5 · 150 / 100% =2,25 Ом.

Исходя из соотношения R=U/I, предел погрешности косвенных измерений вычисляем по формуле (56)

где Δ_U и Δ_I - пределы погрешностей измерений вольтметром и амперметром

Δ_U = ± (2∙ 300/100) = ± 6 В

Δ_I = ± (2,5∙ 25/100) = ± 0,625 А

Тогда получим

Так как Δ_R > Δ^’ _R , делаем вывод, что более точным является результат косвенных измерений.