Орт вектора. Прямоугольный декартовый базис.
Направление любого вектора определяется его ортом.
Определение 3. Единичным вектором или ортом вектора 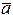 называется вектор
называется вектор 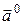 , который имеет одинаковое направление с вектором
, который имеет одинаковое направление с вектором 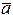 и модуль, равный единице.
и модуль, равный единице.
Очевидным является равенство
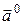 =
= 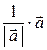 . (4)
. (4)
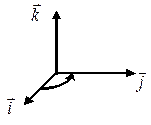 Рис. 6. Рис. 6. |
Рассмотрим три упорядоченных вектора единичной длины (орта) 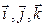 , попарно перпендикулярных и направленных так, что из конца третьего вектора (
, попарно перпендикулярных и направленных так, что из конца третьего вектора ( 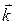 ) кратчайший поворот от первого вектора (
) кратчайший поворот от первого вектора ( 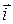 ) ко второму вектору (
) ко второму вектору ( 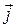 ) виден против часовой стрелки (рис. 6). Такая ориентация векторов называется правой. В противном случае (когда поворот по часовой стрелке) тройка векторов называется лево ориентированной (тройка
) виден против часовой стрелки (рис. 6). Такая ориентация векторов называется правой. В противном случае (когда поворот по часовой стрелке) тройка векторов называется лево ориентированной (тройка 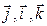 – левая). Очевидно, что векторы
– левая). Очевидно, что векторы 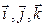 – не компланарны (вектор
– не компланарны (вектор 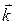 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 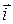 и
и 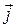 ), поэтому они образуют базис в
), поэтому они образуют базис в 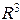 . Этот базис
. Этот базис 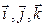 получил название – прямоугольного декартова базиса. Базисом
получил название – прямоугольного декартова базиса. Базисом 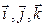 широко пользуются в геометрии и в теории любых прикладных векторных полей. В дальнейшем все преобразования с векторами будут, по умолчанию, производиться в прямоугольном декартовом базисе. На плоскости (в R2) прямоугольный декартовый базис образует пара векторов
широко пользуются в геометрии и в теории любых прикладных векторных полей. В дальнейшем все преобразования с векторами будут, по умолчанию, производиться в прямоугольном декартовом базисе. На плоскости (в R2) прямоугольный декартовый базис образует пара векторов 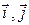 .
.
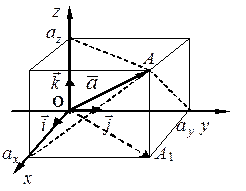 Рис.7. Рис.7. |
Координаты вектора в прямоугольном декартовом базисе имеют простой геометрический смысл. Возьмем произвольный вектор 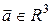 и перенесем начала векторов
и перенесем начала векторов 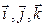 и
и 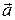 в общую точку О, которая будет началом отсчета (рис. 7). Построим три оси:
в общую точку О, которая будет началом отсчета (рис. 7). Построим три оси: 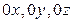 , начало отсчета на которых точка О, а направление и масштаб задают векторы
, начало отсчета на которых точка О, а направление и масштаб задают векторы 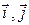 и
и 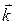 соответственно. Получили прямоугольную декартовую систему координат. На рис. 7 приведено одно из возможных расположений вектора
соответственно. Получили прямоугольную декартовую систему координат. На рис. 7 приведено одно из возможных расположений вектора 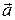 : в первом октанте. Построим параллелепипед, у которого три ребра лежат на осях координат, а диагональю является вектор
: в первом октанте. Построим параллелепипед, у которого три ребра лежат на осях координат, а диагональю является вектор 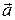 . Тогда по правилу параллелограмма
. Тогда по правилу параллелограмма
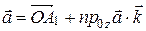 ,
,
где 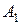 – проекция точки А (конца вектора
– проекция точки А (конца вектора 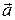 ) на координатную плоскость
) на координатную плоскость 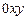 . Вектор
. Вектор 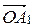 тоже можно разложить на сумму двух векторов по правилу параллелограмма:
тоже можно разложить на сумму двух векторов по правилу параллелограмма:
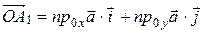 .
.
Тогда разложение вектора 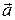 по прямоугольному декартову базису
по прямоугольному декартову базису 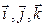 примет вид
примет вид
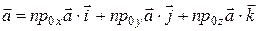 , (5)
, (5)
т.е. координатами вектора являются его проекции на соответствующие координатные оси (направления базисных векторов). Обозначим их 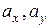 и
и 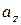 соответственно, тогда
соответственно, тогда 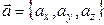 . Если вектор
. Если вектор 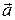 расположен в другом координатном октанте, то некоторые из его проекций, а, следовательно, и координат, будут отрицательными.
расположен в другом координатном октанте, то некоторые из его проекций, а, следовательно, и координат, будут отрицательными.
Найдем координаты орта вектора 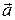 в базисе
в базисе 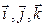 . Из формул (4) и (5) получаем
. Из формул (4) и (5) получаем
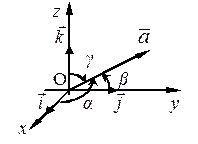 Рис.8. Рис.8. |
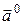 =
= 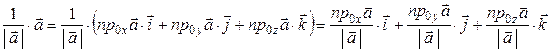
Координатами вектора 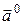 являются коэффициенты при базисных векторах. По теореме 1 отношение проекции вектора на ось к модулю вектора равно косинусу угла между осью и вектором, т. е.
являются коэффициенты при базисных векторах. По теореме 1 отношение проекции вектора на ось к модулю вектора равно косинусу угла между осью и вектором, т. е.
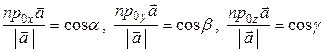 , (6)
, (6)
где α, β, γ – углы между соответствующими осями координат и вектором 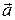 (рис. 8), косинусы этих углов называются направляющими косинусами. Таким образом, координатами орта являются направляющие косинусы
(рис. 8), косинусы этих углов называются направляющими косинусами. Таким образом, координатами орта являются направляющие косинусы
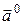 =
= 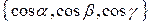 .
.
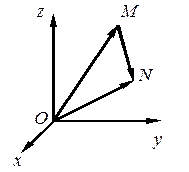 Рис. 9. Рис. 9. |
Любую точку М в пространстве 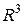 можно задать ее радиус-вектором
можно задать ее радиус-вектором 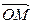 (рис. 9), и рассматривать координаты точки, как координаты ее радиус-вектора. Тогда произвольный вектор
(рис. 9), и рассматривать координаты точки, как координаты ее радиус-вектора. Тогда произвольный вектор 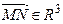 можно представить как разность радиус-векторов
можно представить как разность радиус-векторов
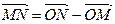
(рис. 9). Если известны координаты конца 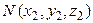 и начала
и начала 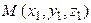 вектора (такие же координаты имеют соответственно векторы
вектора (такие же координаты имеют соответственно векторы 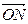 и
и 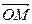 ), то по правилам линейных операций над векторами координатами вектора
), то по правилам линейных операций над векторами координатами вектора 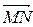 будут
будут
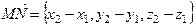 .
.
Итак, чтобы найти координаты вектора, надо из координат конца вектора вычесть соответствующие координаты начала.
