Расчетная схема оценки общей прочности корпуса судна
Нормальная работа КС на волне происходит в условиях упругих деформаций, характеризующихся тем, что при снятии внешней нагрузки форма конструкции корпуса принимает исходное состояние. Для выполнения этого требования производят расчёты прочности корпусных конструкций, в процессе которых определяют действующие в конструкциях напряжения и сравнивают их с допустимыми значениями, принимаемыми с учётом некоторого запаса, именуемого запасом прочности. Запас прочности компенсирует неточности расчёта и возможное превышение действительных эксплуатационных нагрузок по сравнению с принятыми в расчётах.
Помимо внутренних напряжений металл корпуса подвергается внешним деформациям. Если конструкция корпуса жёсткая, то деформации будут малыми. При недостаточной жёсткости конструкции деформации могут быть значительными, вплоть до образования вмятин. Всё зависит от того, как расположена конструкция относительно действующих усилий. Участки возможной концентрации напряжений выявляют ещё на этапе проектирования конструкций корпуса и учитывают дополнительным их подкреплением или устраняют.
Общая прочность судна обеспечивается:
‒ общей продольной прочностью, чтобы уберечь судно от разрушения при продольном изгибе корпуса на волнении, продольном спуске, при постановке судна в док, посадке судна на мель;
‒ общей поперечной прочностью, чтобы обезопасить судно от разлома при кручении корпуса на волнении, при постановке судна в док, поперечном спуске на воду, посадке судна на мель;
‒ местной прочностью, чтобы уменьшить отрицательное воздействие на КС сосредоточенных и распределённых сил, возникающих при приёме и снятии грузов и образующихся в районе грузоподъёмных устройств (кранов, стрел). Эти силы действуют на КС также от реакций кильблоков при постановке в док, реакций спускового устройства при спуске, а также от гидростатического давления воды при аварийных затоплениях отсеков и в ряде других случаев.
При рассмотрении местной прочности корпус рассчитываемого судна разбивают на отдельные конструктивные элементы:
‒ судовые перекрытия;
‒ наружную обшивку;
‒ настил верхней палубы;
‒ двойное дно и двойные борта;
‒ платформы и другие элементы.
Таким образом, общая прочность судна обеспечивается внешней оболочкой, образованной обшивкой корпуса, настилом верхней палубы и продольными водонепроницаемыми переборками с подкрепляющими их рёбрами и связями набора.
Потеря общей прочности ведёт к гибели судна, поэтому расчёту её уделяют особое внимание.
Исходными данными для такого расчёта является интенсивность изменения нагрузки на судно, которая выражается эпюрой (законом) изменения внешних сил, действующих на корпус (рис. 167).
Расчёты, связанные с оценкой общей прочности при продольном изгибе, ведут сначала для положения судна на тихой воде. При этом нагрузку определяют как разность ординат кривых сил тяжести и сил поддержания: q = Р ‒ D (см. рис. 162, 163). При построении этих кривых предполагается, что в пределах теоретической шпации сила тяжести Р от всех составляющих нагрузки в данном сечении КС распределена равномерно, а сила поддержания D, согласно закону Архимеда, уравновешивает её и находится как произведение плотности воды на ускорение свободного падения и объём рассматриваемого отсека: D = ρвgΔV.
Разность ординат указанных кривых представляет собой интенсивность внешней нагрузки в пределах заданного сечения (см. рис. 167), которая выражает смоченную площадь шпангоутов по длине судна Р2(х) = γω(х) в каждый конкретный момент времени. Величину этой площади находят по заранее построенной строевой по шпангоутам (рис. 168). Зная q, при расчётах прочности можно найти действующую в этих условиях перерезывающую силу N0 и изгибающий момент М0|.
 Рис. 167. Эпюры внешних сил, действующих на судно при общем изгибе
Рис. 167. Эпюры внешних сил, действующих на судно при общем изгибе
Строевая по шпангоутам используется для определения координат ЦT погружённых в воду объёмов по длине судна L, что наиболее важно для выявления точек приложения максимальных сил внешней нагрузки. Она представляет собой кривую, ординаты которой в принятом масштабе равны погружённым в воду площадям шпангоутов по заданную ватерлинию, а абсциссы — положению шпангоутов по длине судна.
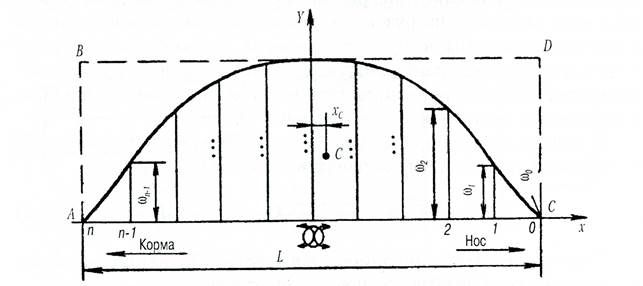
Рис. 168. Строевая по шпангоутам
По площади под кривой, представленной на рис. 168, определяется объёмное водоизмещение судна V, а по отношению площадей прямоугольника ABDC и AYC — коэффициент продольной полноты объёмного водоизмещения φ = δ/β. Абсцисса ЦТ площади строевой равна абсциссе ЦВ судна.
Водоизмещение судна можно определить также путём построения кривой, называемой строевой по ватерлиниям, площадь под которой численно равна объёмному водоизмещению судна при данной осадке. Свойства этой строевой таковы, что ордината ЦТ площади под кривой равна возвышению ЦВ судна над основной линией, а коэффициент полноты площади равен коэффициенту вертикальной полноты судна при данной осадке.
По действующим на судно силам Р1(х) и Р2(х) (см. рис. 167) определяют изгибающий момент Мизг, который и используется для проверки общей продольной прочности корпуса. При предварительном проектировании корпуса расчётный (наибольший) изгибающий момент приближённо определяется по формуле
 (13)
(13)
где D — водоизмещение, т;
L — длина судна, м;
К — коэффициент, равный:
28-33 — для крупных сухогрузных судов;
24-28 — для малых сухогрузных судов с МО в средней части;
38-43 — для крупных танкеров;
32-38 — для малых танкеров.
Однако в реальных условиях при качке на судно действуют дополнительные нагрузки, вызванные перераспределением сил поддержания и изменением инерционных и гидродинамических сил. Основная часть этих нагрузок обусловлена положением ватерлинии и изменением формы погружённого объёма. Поэтому для их определения приходится строить вторую кривую — строевую по ватерлиниям, ординаты которой в принятом масштабе показывают площадь ватерлинии в зависимости от углубления КС.
С учётом этих дополнительных сил наибольшие величины перерезывающей силы N и изгибающего момента М будут равны:
N = N0 + ΔN; M = M0 + ΔM. (14)
Они проявляются при длине волны, близкой к длине судна, при положении судна на вершине и подошве волны.
Под воздействием момента М происходит изгиб корпуса, и в продольных связях палубы и днища возникают продольные нормальные напряжения σп, σдн. Для оценки величины этих напряжений в первом приближении производят расчёт эквивалентного бруса (рис. 169, а-г), т. е. такой условной балки, площадь поперечного сечения которой равна сумме площадей всех продольных связей, участвующих в общем изгибе и сосредоточенных у ДП, с учётом их протяжённости, наличия в них вырезов и т. д. При этом в качестве материала этих связей на палубе и днище использован серийный прокат, имеющий определённые размеры (обычно прямоугольные). Площадь и момент инерции каждого метра его внесены в справочники и заранее известны, поэтому не представляет труда найти общую площадь и момент инерции поперечного сечения всего корпуса.

Рис. 169. Эквивалентный брус и напряжения в корпусе:
а - поперечное сечение судна; б - эквивалентный брус; в - нормальные напряжения;
г - касательные напряжения
Замена судна на эквивалентный брус позволяет рассматривать судно как жёсткую безопорную балку, работающую на изгиб. Подобное упрощение модели расчёта даёт возможность определять нормальные и касательные напряжения в поперечном сечении судна, называемые напряжениями от общего изгиба, с помощью элементарной теории изгиба балок по формулам сопротивления материалов.
Эквивалентный брус наглядно показывает, как распределяется площадь сечения конструктивных связей корпуса, принимающих участие в сопротивлении продольному изгибу по высоте. Размеры балок, образующие конструктивные элементы корпуса, выбираются по справочникам в зависимости от площадей поперечного сечения проката нужного сортамента, наименьшим моментам их сопротивления или моментам инерции сечения профилей относительно центральной горизонтальной оси о-о (рис. 169). Эти параметры указываются в Правилах Регистра для балок из катаных или составных профилей с присоединёнными условными поясками обшивки (см. рис. 169, а).
Влияние параметров полотнищ палубы, бортов и днища, примыкающих к пояскам продольных связей, учитывается с помощью редукционных коэффициентов.
Установив связи эквивалентного бруса, рассчитывают его момент инерции J, определив предварительно собственные и переносные моменты инерции всех составляющих его продольных связей относительно оси о-о.
Таким образом, полный момент инерции стандартных и нестандартных профилей балок, используемых в палубных и днищевых перекрытиях КС, будет равен
J = Σ J0 + ΣS0(li - l0). (15)
Разделив величину J на отстояние наиболее удалённых от нейтральной оси связей-балок палубы и днища lп и lдн, устанавливают моменты их сопротивления

 . (16)
. (16)
Из-за сложности поперечного сечения КС определение момента сопротивления сечения связано с некоторыми затруднениями, так как необходимо найти площади всех продольных связей, участвующих в общем изгибе, с учётом их протяжённости и наличия в ней вырезов, что требует кропотливой работы.
Прочность каждой связи на эквивалентном брусе проверяют в сечениях, отстоящих от нейтральной оси на расстоянии х, сопоставляя действующие в ней нормальные напряжения с допускаемыми:
 (17)
(17)
Напряжения в палубных и днищевых связях определяются при х = l1 и х = l2:

 (18)
(18)
В промежуточных связях напряжения меняются по закону прямой линии (см. рис. 169, в), а у нейтральной оси они равны нулю. Таким образом, наибольшие напряжения возникают в верхней палубе и днище судна. При перегибе судна в верхней палубе появляются напряжения растяжения, а в днище — сжатия, при прогибе — наоборот.
Перерезывающие силы вызывают касательные напряжения, распределяемые по закону
 (19)
(19)
где Q — перерезывающие силы в сечении судна, кг;
S — статический момент площади (заштрихованной на рис. 169,б) относительно оси о-о, см2;
J — момент инерции, см4;
b — ширина сечения судна, равная ширине сечения эквивалентного бруса, см.
Касательные напряжения достигают максимума у нейтральной оси, а у крайних волокон — минимума (в связи с уменьшением S). В промежуточных сечениях касательные напряжения распределяются по высоте так, как показано на рис. 169, г. По длине же судна они достигают наибольшего значения там, где действуют наибольшие перерезывающие силы, т. е. приблизительно на¼ и ¾ длины судна от оконечностей.
Однако окончательный расчёт производят при положении судна в реальных условиях, когда величина изгибающего момента Мизг зависит от положения судна относительно профиля волны и достигает наибольших значений на вершине и подошве волны.
Под воздействием момента Мизг происходит изгиб корпуса и в продольных связях возникают продольные нормальные напряжения, которые определяются по формуле
 (20)
(20)
где W — момент сопротивления поперечного сечения, соответствующий положению рассматриваемой связи, м см 2.
Для определения нормальных напряжений от продольного изгиба палубы σп и днища σдн достаточно разделить действующий в районе миделя изгибающий момент на моменты сопротивления палубы Wп и днища Wдн :

 (21)
(21)
Максимальные нормальные напряжения от изгиба будут проявляться в крайних связях корпуса — в районе соединения палубы с бортом. Их знак определяется знаком момента; растягивающие напряжения принимают за положительные. На нейтральной оси нормальные напряжения обращаются в нуль, а касательные, наоборот, достигают своего наибольшего значения в бортовой обшивке.
Наибольшие касательные напряжения при продольном изгибе возникают в сечениях, расположенных в районе четверти длины судна от оконечностей. Величину этих напряжений определяют по формуле
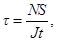 (22)
(22)
где N — суммарная перерезывающая сила;
S — статический момент площади сечения связей относительно нейтральной оси по одну сторону от точки, для которой вычисляются напряжения;
J — момент инерции стандартных профилей поперечных сечений судовых конструкций, принимаемый по специальным таблицам;
t — суммарная толщина продольных связей на данном уровне.
При проектировании судна исходят из компромиссных требований: общую продольную прочность всего судна необходимо обеспечивать не за счёт утяжеления его корпуса, а, наоборот, — за счёт его облегчения на основе применения высокопрочных материалов, что, однако, ведёт к удорожанию проекта. Для обеспечения местной прочности необходимо искать другие пути, в частности, оптимально распределять металл пo поперечным сечениям как отдельных конструктивных элементов, так и корпуса в целом.
Наиболее сложным является прочностной расчёт плоского перекрытия, опирающегося на прямоугольный контур, который представляет собой сложную статически неопределимую систему. Расчёт такого контура выполняется при условном допущении, что вся внешняя нагрузка по периметру приложена только к ряду балок главного направления с реакциями внешних перекрёстных связей. Если балки набора расположены в одной плоскости и жёстко соединены между собой в узлах, то они представляют собой плоские рамы, которые воспринимают нагрузки в той же плоскости. На рис. 170 представлена простая шпангоутная рама, состоящая из флора, двух шпангоутов и бимса, соединяемых в четырёх узлах. Она рассчитывается методом трёх моментов, как и для неразрезных балок.
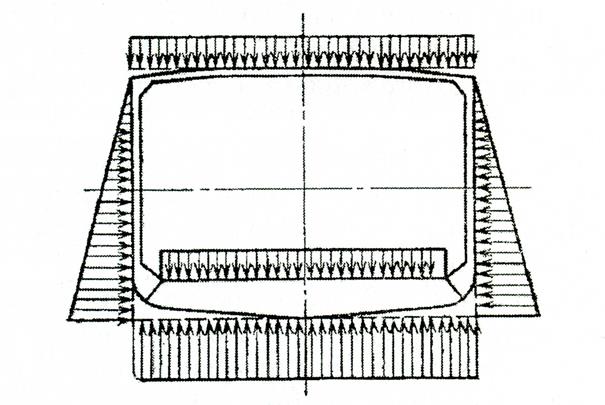
Рис. 170. Схема нагрузок, действующих на шпангоутную раму и перекрытия корпуса
У сложных рам в одном узле сходится более двух балок. Для облегчения расчёта таких балок на общий изгиб конструкцию рамы упрощают, приведя её к одному из существующих профилей с нормированными прочностными данными.
При определении размеров прочных связей по Правилам Регистра исходят из размеров составных частей корпуса в зависимости от его главных размерений, а также учитывают назначение судна и район его эксплуатации. В частности, если судно будет плавать в мелкобитом льду в лёгких ледовых условиях неарктических морей, ему присваивают соответствующий класс с подкреплением корпуса. Более значительные подкрепления корпуса предусмотрены для судов, плавающих в мелкобитом льду северных неарктических морей типа Белого. Если судно предназначено для плавания в битом льду арктических морей в течение всей навигации, то его корпус подкрепляют ещё больше и присваивают класс ЛУ. И, наконец, самые мощные ледовые подкрепления имеют КС, предназначенные для самостоятельного плавания в арктических и антарктических морях при толщине льда до 0,5 м, а также в крупнобитом льду или за ледоколом; им присваивают класс ЛУ7 и выше. Специальные ледовые подкрепления предусмотрены также для речных ледоколов, плавающих в замерзающих северных реках.
