Судна после приёма в промежуточном порту палубного груза.

Груз размещается на люковых крышках. Высота штабеля равна 2,8 м, ширина равна ширине крышки люка.

Принимаем палубный груз. Так как грузоподъемность использована полностью (М=5025 т), то условно считаем, что с судна выгружено в промежуточном порту 100 т груза таким образом, что его центр тяжести не изменился, и принят палубный груз в количестве 100 т.

В нашем случае масса палубного груза: m_гр = 100 т

Аппликата центра тяжести принимаемого на палубу груза вычисляется по формуле:

Z_гр = H+h_kом+1,4 (4.1)

где Н - высота борта судна, H=6 м (по первой части);

h_kом - высота комингса люка, определяем по схематическому чертежу судна (Рисунок 1.1) с учетом масштаба по высоте h_k=1,3 м , тогда

Z_гр=6+1,3+1,4=8,7 м

Абсциссу центра тяжести палубного груза x_гр определим из условия, что абсцисса центра тяжести судна не изменилась. Для этого вычтем в формуле (2.2) в числителе момент 100·X_i, а в знаменателе m_гр=100 т, т.е. разгрузим судно и загрузим судно (где X_i – это абсцисса центра тяжести 2-го трюма - см. таблицу 2.1).

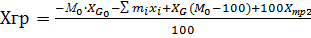(4.2)

X_гр =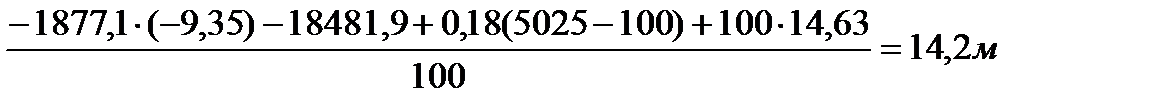

Длину груза определим, учитывая допустимое давление на крышки люков (таблица 2.1). Площадь груза определяется по формулам:

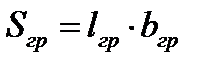(4.3)

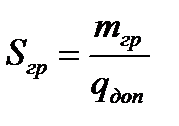(4.4)

где S_гр, l_гр, b_гр – соответственно площадь, длина и ширина палубного груза, м;

q_доп – допустимое давление на крышки люков (таблица 2.1).

Получаем:

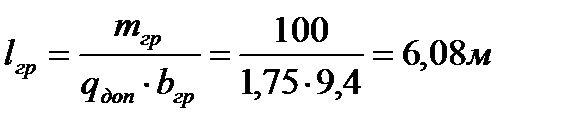(4.5)

Так как принимаемый палубный груз "малый" используем формулу для приёма и снятия малого груза:

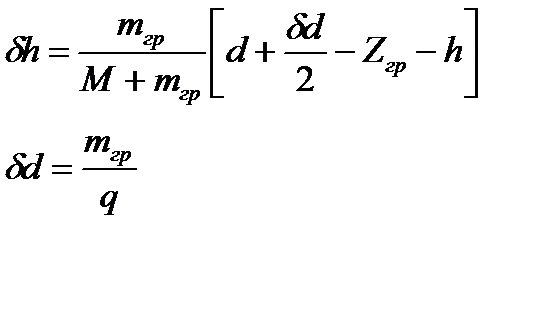(4.6)

где q - число тонн, изменяющих осадку на 1 см,

q=13,77 т/см (определяется по Приложению Г[1]);

М =5025 т,

h=2,27 м (см. часть 2)

d=4,13 м (см.часть 1)

z_гр= 8,7 м

dd= 100/13,77=7,26 см = 0,0726 м, тогда

dh=100/(5025 + 100 - 100) · (4,13 + 0,0726/2 - 8,7 - 2,27) = -0,14 м,

тогда метацентрическая высота судна с палубным грузом будет вычисляться по формуле:

h₁ = h + dh (4.7)

где h - метацентрическая высота (см. часть 2)

h₁= 2,27-0,14 = 2,13 м 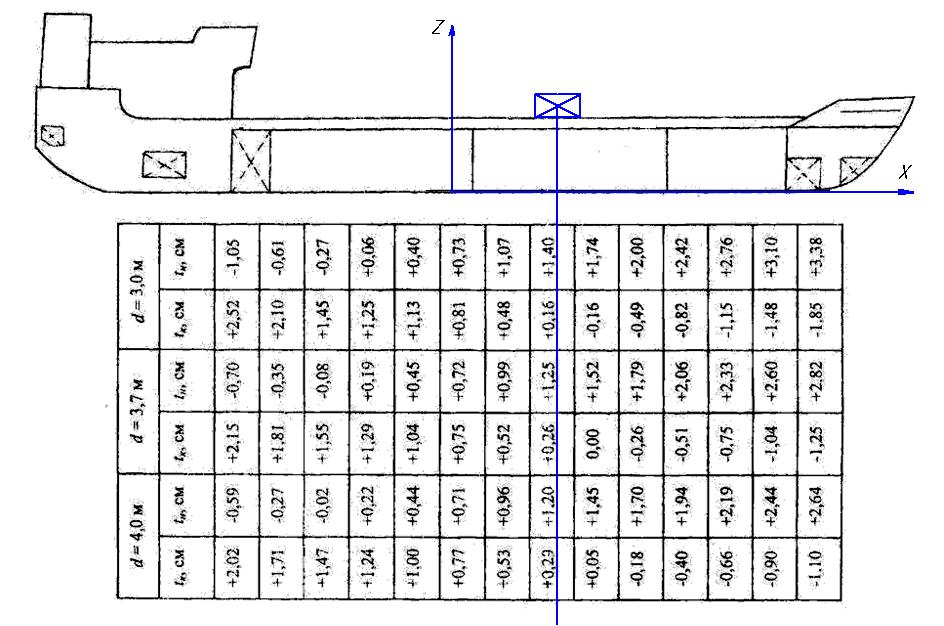Рисунок 4.1 – Изменение осадки от принятия/снятия 10 тонн груза

Изменения осадок носом и кормой при приёме груза находят по формулам:

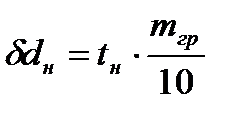(4.8)

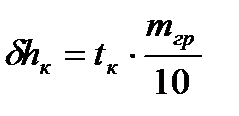(4.9)

Значения t_н и t_k определяются с помощью таблицы изменений осадки от приёма 10 т груза (Рисунок 4.1).

Из таблицы Рисунка 4.1 для осадки d = 4 м получаем значения

t_н и t_k; t_н = 1,20 см и t_k = 0,29 см, тогда

dd_н = 1,20·100/10=12,0 см

dd_к = 0,29·100/10 =2,9 см

4.2. Определение угла крена судна от неудачно размещённого груза массой mгр=100тс координатой у=-0,50 м.

Если груз размещён неравномерно по ширине, то судно получит статический крен, который определяется формулой:

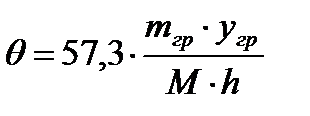, (4.10)

где m = 100 т - масса неудачно размещённого груза;

у = - 0,50 м - координата неудачно размещённого груза;

h = 2,27 м - метацентрическая высота (см. часть 2)

М = 5025 т - водоизмещение судна,

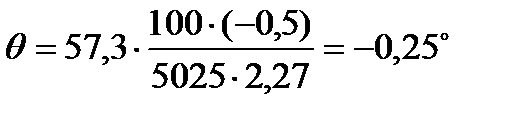
Получаем: 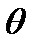= - 0,25^о

Угол крена в формуле (4.10) получился отрицательным, это значит, что судно имеет крен на левый борт.

4.3. Определение статических и динамических углов крена от шквала, создающего кренящий момент 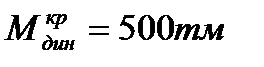, при бортовой качке с амплитудой .

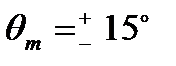Углы крена определяется с помощью диаграмм статической и динамической остойчивости (Рисунки 4.2 - 4.7)

Плечо кренящего момента находят по формуле:

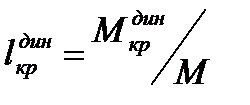(4.11)

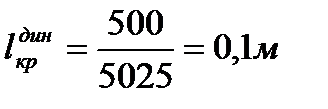
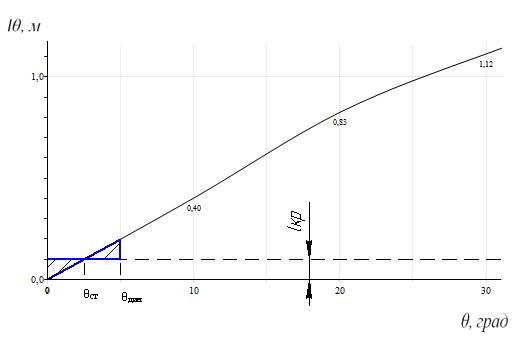Рисунок 4.2 - Диаграмма статической остойчивости при отсутствии крена

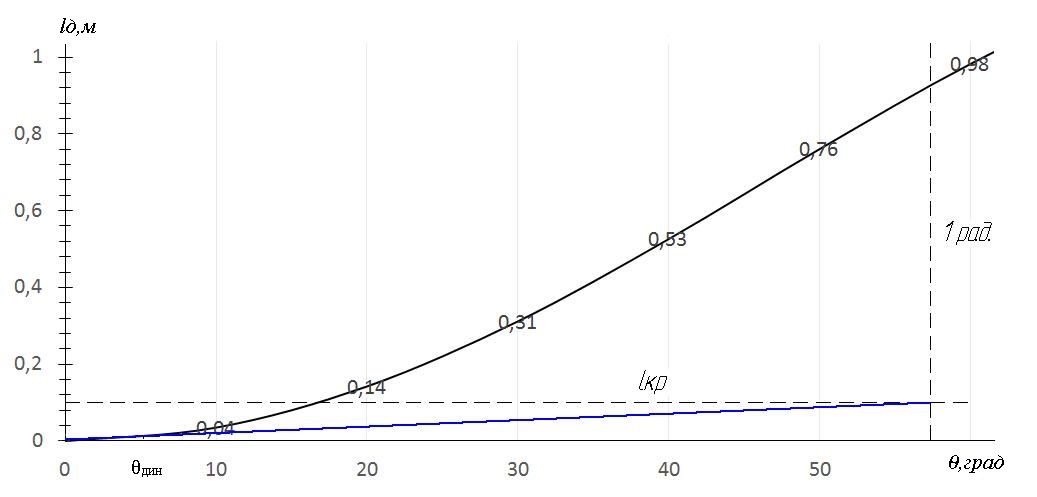Рисунок 4.3 - Диаграмма динамической остойчивости при отсутствии крена 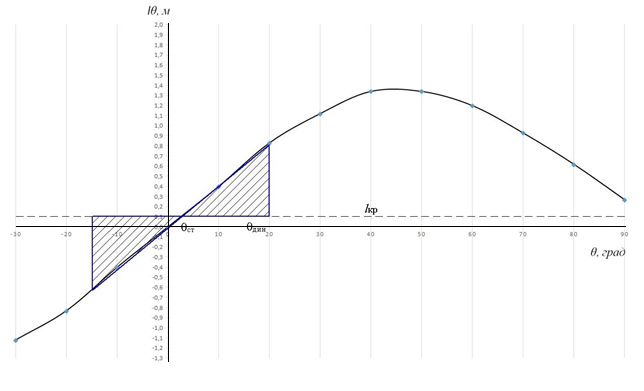Рисунок 4.4 - Диаграмма статической остойчивости при крене на наветренный борт

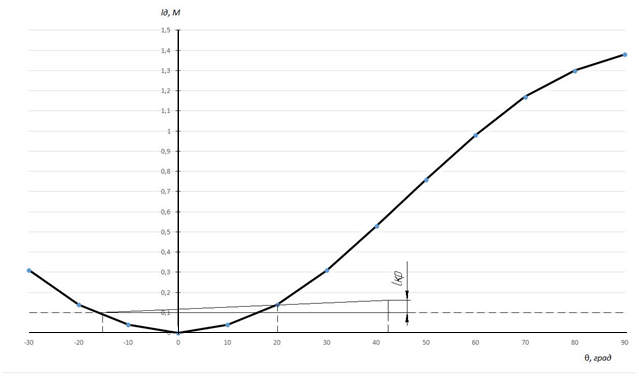Рисунок 4.5 - Диаграмма динамической остойчивости при крене на наветренный борт. 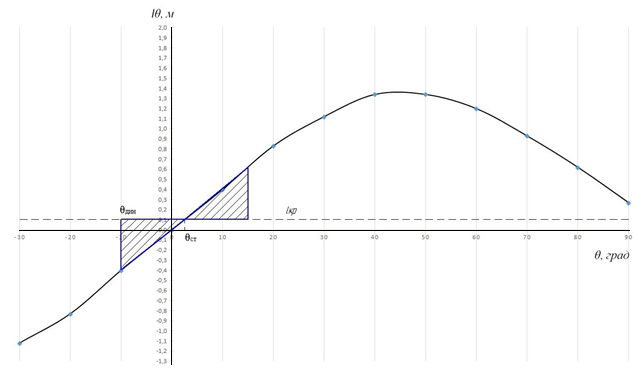Рисунок 4.6 - Диаграмма статической остойчивости при крене на подветренный борт.

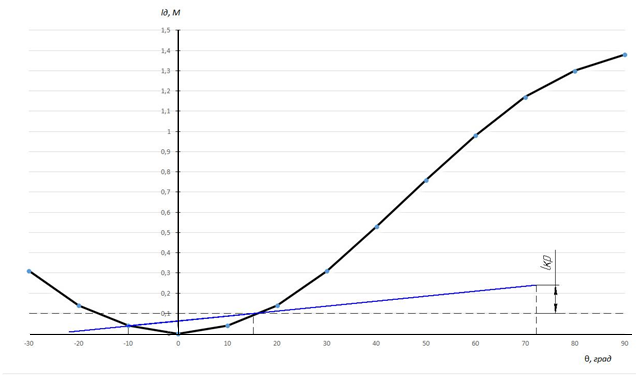
Рисунок 4.7 - Диаграмма динамической остойчивости при крене на подветренный борт.

На диаграмме статической остойчивости динамический угол крена определяют из условия равенства работы восстанавливающего и кренящего моментов. Работа восстанавливающего момента равна площади, ограниченной графиком диаграммы статической остойчивости, осью абсцисс и перпендикуляром к ней, восстановленном из точки Ɵ_д. Работа кренящего момента равна площади, ограниченной графиком кренящего момента до угла крена Ɵ_д осью абсцисс. Положение перпендикуляра при Ɵ_д подбирается таким образом, чтобы площади под диаграммой статической остойчивости и графиком кренящего момента были равны.

По диаграмме динамической остойчивости задача решается следующим образом. На оси абсцисс диаграммы откладывается угол, равный 1 радиану (57,3°), и из полученной точки восстанавливается перпендикуляр. На перпендикуляре откладывается плечо кренящего момента 1^дин_кр, конец этого отрезка соединяется с началом координат. Абсцисса точки пересечения этой прямой с диаграммой динамической остойчивости соответствует углу динамического крена судна от шквала.

Снимая на диаграммах статической и динамической остойчивости значения статического и динамического углов крена, получаем:

При наличии у судна крена на тихой воде по диаграмме статической остойчивости (Рисунок 4.2) Ɵ_ст=2,5⁰, Ɵ_д = 5⁰ и по диаграмме динамической остойчивости (Рисунок 4.3) Ɵ_д = 5⁰.

При крене судна на наветренный борт по диаграмме статической остойчивости (Рисунок 4.4) Ɵ_ст=-15⁰, Ɵ_д = 20⁰ и по диаграмме динамической остойчивости (Рисунок 4.5) Ɵ_д = 20⁰.

При крене судна на подветренный борт по диаграмме статической остойчивости (Рисунок 4.6) Ɵ_ст=15⁰, Ɵ_д = -10⁰ и по диаграмме динамической остойчивости (Рисунок 4.7) Ɵ_д = -10⁰.

Таким образом, можем сделать вывод, что во время шквального ветра динамические углы будут больше в том случае, когда на волнении судно накреняется на наветренный борт. Эта ситуация принимается за расчётную при нормировании их остойчивости.

4.4 Проверка удовлетворения требований остойчивости судна в