Информационный подход к оценке качества оптических изображений

При проектировании автоматизированных систем обработки и передачи изображений различного назначения одним из основных требований, предъявляемых к ним, является обеспечение заданного качества получения и воспроизведения изображений, что требует выбора количественного критерия для его объективной оценки. По общепринятой методологии количественная оценка (измерение) характеристик любого физического объекта или явления подразумевает определение некоей меры их оценки и выбор единиц измерения этой меры. В связи с чем и количественная оценка качества изображения, как характеристики оптического изображения, требует выбора меры для оценки качества изображения и единиц ее измерения.

В большинстве применяемых в настоящее время критериев оценки качества черно-белого изображения за меру этой оценки принимается разрешающая способность (QR), которая зависит как от пространственного разрешения изображения, характеризующегося максимально возможным количеством различимых черных и белых линий на единицу длины, так и от фотометрического разрешения (контраста), оценивающегося числом различимых уровней (градаций) используемой оптической характеристики изображения, например, оптической плотности. Числовой интегрированной оценкой качества изображения при указанном подходе выступает частотно-контрастная характеристика (ЧКХ), определяющая максимальное число различимых черных и белых линий на единицу длины при заданном контрасте. [1,2]

Однако из анализа критериев оценки качества изображений, основанных на разрешающей способности, следует ряд замечаний.

Во-первых, практическое применение критериев QR часто ведет к завышению разрешающей способности изображений и, как следствие, их качества, вызванное субъективными особенностями этих методов, которые проявляются в следующем:

- линейные объекты разрешаются глазом значительно лучше, чем точечные [2];

- часто интересующие наблюдателя объекты имеют меньший контраст, чем контраст черного и белого при использовании стандартных мир, например при обработке изображений звездного неба;

- анализ изображения, как правило, проводится на некотором его фрагменте и в силу специфики зрения, заключающейся в обобщении и домысливании, получаемое разрешение оказывается больше, чем разрешение изображения того же качества, состоящее из двух отдельных точек (семантическая оценка).

Во-вторых, критерии на основе QR не позволяют однозначно учесть влияние условий получения изображений на их качество. Например, установить, какое из двух изображений с точки зрения качества лучше: полученное на фотоматериале с высоким пространственным разрешением и низким фотометрическим разрешением или изображение, зарегистрированное на фотоматериале с низким пространственным разрешением и высоким фотометрическим разрешением.

В-третьих, следует отметить, что хотя критерии QR и позволяют оценить качество конкретного изображения, которое может варьироваться в весьма широких пределах в зависимости от объекта и условий съемки, тем не менее они не позволяют установить граничные значения параметров, характеризующих качество изображения с учетом заданных условий и целей их получения.

В-четвертых, оценка качества изображения по критерию QR, как правило, не является корректной, так как оба вида разрешения: пространственное и фотометрическое - взаимозависимы [1,3].

И, наконец, следует отметить, что практическая оценка качества изображения по критерию QR (например, путем впечатывания в него стандартных мир) подразумевает, что определяемое таким образом качество изображения, как и само изображение, считается детерминированным и статическим, хотя реально оцениваемое качество изображения, как было указано выше, может варьироваться в зависимости от условий получения изображения и целей использования.

Перечисленные замечания не позволяют осуществить всесторонне объективную оценку качества изображения по критерию QR.

Другой подход к выбору критерия оценки качества изображения может быть основан на том факте, что любое изображение представляет собой заданного вида сообщение, содержащее информацию о каком-либо объекте или процессе и зависящее от условий формирования этого изображения. При этом за меру оценки качества изображения предполагается принять наибольшее количество информации, которое может в нем содержаться, а за единицу измерения этой меры количество информации, выраженное в битах, отнесенное к единице площади изображения, то есть энтропию изображения. В дальнейшем введенный таким образом критерий оценки качества изображения будем определять как энтропийный и обозначать его QI.

Критерий QI позволяет, во-первых, для каждого конкретного изображения при оценке его качества учитывать условия его формирования, и, во-вторых, если данное изображение подвержено дальнейшей обработке или преобразованию, то повторное применение этой оценки к изображению, полученному после указанных операций, дает возможность установить потерю информации или степень ее использования.

С физической точки зрения изображение можно охарактеризовать как результат отображения на фиксированный момент времени и заданной ограниченной поверхности (плоскости) совокупности интегральных источников излучения или отражения, расположенных вне заданной поверхности. Данное толкование позволяет перейти к информационному подходу представления изображения, по которому изображение - это результат преобразования, передачи и воспроизведения информации, содержащейся в источнике визуального сообщения (излучающей или отражающей поверхности). При этом предполагается, что источник визуального сообщения (ИВС) в каждый момент времени соответствует одному из символов алфавита, рассматриваемого источника (изображению), характеризующему пространственное распределение интегральных потоков лучистой энергии, излучаемых (или отражаемых) отдельными элементарными участками излучающей поверхности.

Информационный подход представления изображения и введенный критерий QI позволяют отождествить понятие качества оптического изображения с максимальным количеством информации, содержащимся в символе ИВС, где под символом ИВС (изображением) традиционно понимается любое мгновенное состояние ИВС, характеризующееся мгновенным распределением энергии и спектрального состава излучения, генерируемого элементарными участками ИВС.

Для получения расчетных формул оценки качества оптического изображения по критерию QI ограничим область задания изображения прямоугольным участком Q, разбитым регулярной квадратной сеткой на элементарные участки 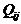(пиксели, элементы разложения) такого размера, что в каждом из них значение рассматриваемого информационного параметра оптического изображения, например, яркости (U) является постоянным (рис.1.6).

Q11
Q
			Qij

Рис. 1.6

Отметим, что такое разбиение всегда можно выполнить, так как любому реальному процессу или явлению свойственна инерционность (то есть конечное время или пространство переходного процесса) и поэтому всегда будет существовать достаточно малая, но конечная часть изображения, которую можно считать интегральным источником оптического сообщения. Предполагая, что значения 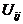равновероятны и некоррелированы (в этом случае энтропия максимальна), количество информации (I), содержащееся в любой подобласти 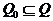, обладающей площадью 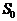, можно найти исходя из определения количества информации по Хартли согласно формуле:

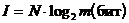, (1.6)

где 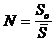- общее число пикселов, содержащихся в подобласти ;

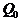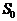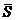, - значения площадей соответственно подобласти 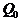и пиксела ;

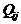m - объем алфавита пикселов, то есть количество различимых дискретных значений информационного параметра U.

Очевидно, что для любых реальных ИВС число дискретных значений информационного параметра - конечно, так как при их формировании всегда присутствуют шумы, обусловленные молекулярной структурой физических объектов и квантовой природой лучистой энергии. Поэтому, если известен интервал допустимых значений информационного параметра (U) и величина шума ( 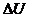), то значение m может быть определено из соотношения:

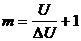. (1.7)

В результате соотношение (1.6) преобразуется к виду:

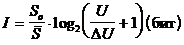, (1.8)

а максимально возможное количество информации, содержащееся в ИВС площадью 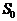, будет определяться выражением:

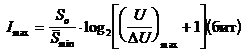. (1.9)

Если выбрать подобласть Q единичной площади ( 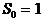), то максимально возможное количество информации (H), содержащейся в ней

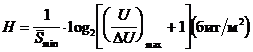. (1.10)

может служить численной оценкой качества изображения.

Таким образом, величина H, характеризующая качество изображения по критерию QI, определяется двумя параметрами: площадью минимально различимого элемента разложения (пиксела) 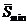и максимальным значением отношения сигнал/шум .

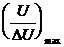Нахождение этих параметров на практике затруднено, так как они, во-первых, коррелированы, а, во-вторых, зависят от условий формирования изображения. Действительно, при уменьшении площади элемента разложения ИВС отношение сигнал/шум падает, а уменьшение освещенности ведет и к падению отношения сигнал/шум, и к увеличению размеров минимального различимого элемента разложения площадью .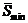

Определить функциональную связь между площадью элемента разложения ( 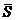) и отношением сигнал/шум 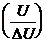, а также их зависимость от условий освещенности возможно, исходя из квантовой теории света, согласно которой оптический луч представляет собой поток фотонов. Таким образом, любой ИВС можно рассматривать как некую поверхность, каждый элемент разложения которой 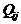излучает (или отражает) фотоны с различной интенсивностью( 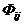), т.е.

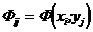, (1.11)

где 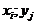- декартовы координаты элемента разложения .

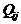Несамосветящиеся ИВС могут генерировать символы визуальных сообщений только в том случае, если они освещены и отражают падающий на них некий равномерный поток фотонов.

Интенсивность ( 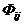) определяется как количество фотонов ( 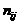), излученных элементом разложения 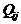площадью 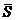за время :

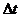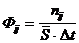. (1.12)

Таким образом, любой источник оптических сообщений (F) при заданном 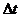можно представить в виде совокупности элементов разложения 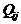, каждый из которых излучает определенное число ( 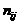) квантов света, то есть

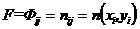при 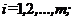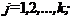(1.13)

Представляет интерес определение минимального числа фотонов в этом потоке, которое обеспечит получение ИВС и соответствующего изображения с заданным качеством.

Очевидно, что минимальное количество равномерно распределенных падающих фотонов ( 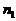), необходимое для построения любого контурного (содержащего только два уровня яркости) ИВС, состоящего из N элементов разложения, будет

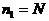. (1.14)

Но если требуется получить полутоновый ИВС и соответствующее ему полутоновое изображение с некоторой заданной минимальной различимой разностью яркостей (минимальным контрастом) элементов разложения (с), или с заданным числом градаций и отношением сигнал/шум 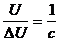, то минимальное количество фотонов ( 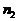), необходимое для построения такого изображения, должно быть равным:

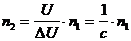, (1.15)

где

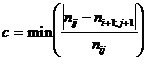, при i=1,2,….m; j=1,2,….k.

Излучение фотонов, а, следовательно, и их падение на некоторую площадку подчиняется квантовым законам и носит случайный характер, подчиняющийся, как известно, закону распределения Пуассона [4], из которого следует, что вероятность количества фотонов 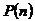, испускаемых каким-либо светящимся телом за время T, описывается выражением:

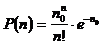, (1.16)

где 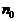- среднее значение количества испускаемых фотонов.

Поэтому очевидно, что в действительности число фотонов, падающих на каждый элемент разложения за время T, распределено вокруг среднего значения 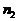так, что среднеквадратичное отклонение (в соответствии с распределением Пуассона) равно 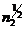, то есть среднеквадратическое значение шума будет равно 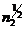. Если при этом отношение сигнал/шум ( 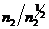) будет больше с, то получить изображение с заданным минимальным контрастом (c) невозможно. Поэтому необходимо повышать минимальное число падающих фотонов, чтобы уровень шума не превышал заданный минимальный контраст, то есть минимальное число фотонов, падающих на элемент разложения ИВС, должно быть увеличено до величины 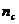, такой, чтобы выполнить условие:

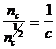(1.17)

и, следовательно,

.

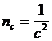В этом случае общее число фотонов, приходящееся на весь ИВС, возрастет до :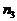

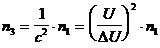. (1.18)

Для подсчета минимального количества фотонов, падающих на ИВС и обеспечивающих получение изображения с заданным минимальным контрастом необходимо учитывать еще один фактор.

При обработке изображений, соответствующих символам визуальных сообщений, как правило, считают, что их минимально различимый контраст соответствует среднеквадратическому значению шумовых флуктуаций. Однако это не значит, что мгновенное значение шума в этом случае не будет превышать принятого уровня минимально различимого контраста, так как мгновенное значение шума может значительно превышать его среднеквадратичное значение.

Поэтому при обработке изображений, состоящих из большого числа элементов разложения, необходимо, чтобы минимально различимый контраст соответствующих символов визуального сообщения существенно превышал среднеквадратичный уровень шума, вызванного флуктуацией потока падающих фотонов.

Величину превышения легко оценить, аппроксимируя статистическое распределение числа падающих фотонов нормированным нормальным законом распределения, кривая распределения которого ( 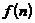) представлена на рис.1.7, а ее аналитическое выражение может быть приведено к виду

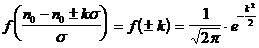, (1.19)

где s - среднеквадратическое отклонение от среднего значения ( );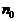

k =1,2,...

Вероятность того, что значение числа падающих световых фотонов на отдельный пиксел ( 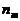) будет отличаться от среднего значения ( 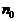) на величину более чем ks определяется выражением:

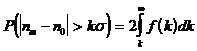. (1.20)

В табл.1.1 приведены численные значения этой вероятности при различных k.

Табл. 1.1

k
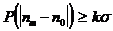	0,32	0,046	0,27·10-3	6,3·10-5	5,7·10-7	2,0·10-9	2,5·10-12

Таблица 1.1 позволяет определить необходимую кратность превышения минимально различимым контрастом среднеквадратичного значения шума флуктуации числа падающих фотонов при заданной вероятности ложного его измерения. Например, для получения изображения с заданным минимальным контрастом и вероятностью ложного его измерения не более 1% необходимо, чтобы значение заданного минимального контраста не менее чем в 3 раза превышало среднеквадратическое значение флуктуации числа падающих фотонов.

Следовательно, для уменьшения до допустимого значения вероятности ложного измерения информационного параметра элементов разложения ИВС необходимо еще больше увеличивать среднее число падающих на них фотонов, тем самым увеличивая отношение сигнал/шум.

В случае распределения Пуассона при среднем значении числа падающих фотонов 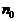среднеквадратичное значение шума равно 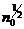, а отношение сигнал/шум -

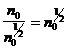. (1.21)

Поэтому для увеличения отношения сигнал/шум ( 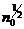) в k раз среднее число падающих фотонов необходимо увеличить в 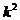раз, таким образом, минимальное число фотонов ( 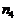), которое необходимо для получения изображения, состоящего из N элементов разложения, с контрастом с можно найти из выражения:

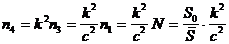, (1.22)

а соответственно число фотонов, приходящихся на один элемент разложения ( 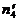) будет определяться равенством:

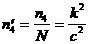. (1.23)

Для экспериментального подтверждения полученного теоретического соотношения (1.22) были выполнены экспериментальные исследования, которые заключались в фоторегистрации изображения специального тест-объекта, предложенного в работе [3], при различных условиях съемки.

Тест-объект представляет собой белое поле, на котором размещались черные круги, причем вдоль строк круги имели по сравнению с фоном одинаковый контраст, но различные диаметры ( 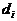): диаметр каждого последующего в два раза меньше предыдущего, а по столбцам были размещены круги одного диаметра, но контраст ( 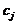) каждого последующего был в два раза меньше предыдущего. В этом случае произведение 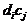остается постоянным вдоль линий, параллельных диагонали тест-объекта.

На рис.1.8 представлены зарегистрированные изображения тест-объекта, полученные при постоянной освещенности, но различных временах экспозиции, причем каждое последующее изображение получено при экспозиции в 4 раза большей, чем предыдущее.

Рис. 1.8

Из соотношения (1.22) следует, что при постоянных условиях съемки

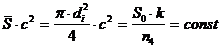. (1.24)

А так как число падающих на тест-объект фотонов ( 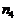) соответствует величине экспозиции (B), то можно считать, что произведение 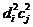обратно пропорционально величине экспозиции:

.

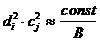Следовательно, для того, чтобы граница различимых дисков на зарегистрированном изображении тест-объекта сдвинулась на один диск вправо ( 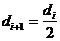; 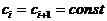) или чтобы граница различимых дисков сдвинулась на один диск вниз ( 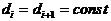; 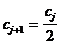) необходимо увеличить экспозицию в 4 раза.

Анализируя полученные фотоизображения тест-объекта, можно сделать вывод, что разрешение элементов изображения при заданной экспозиции зависит как от их размера ( 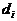), так и от контраста ( 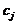), и хорошо согласуется с полученным теоретическим соотношением (1.22).

Действительно, при увеличении экспозиции в 4 раза граница различимых дисков смещается на один шаг вправо, в сторону дисков с диаметром в 2 раза меньше, и на один шаг вниз, в сторону дисков с контрастом в 2 раза меньшим, как и следует из соотношения (1.22).

Для практического использования полученных соотношений (1.22, 1.23) целесообразно привести их к общепринятому виду, то есть к виду с использованием энергетических и светотехнических характеристик. Известно, что падение за время 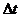на некоторую площадку площадью 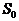числа фотонов n с частотой n соответствует притоку энергии Q [5]:

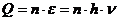, (1.25)

где 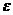- энергия одного фотона;

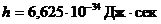- постоянная Планка.

В случае немонохроматического излучения в диапазоне частот от 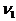до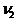

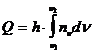, (1.26)

где 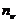- распределение числа фотонов по частоте n.

В этом случае энергетический и светотехнический поток излучения ( 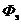и 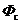соответственно) определяют по формулам

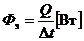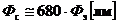; , (1.27)

а освещенность энергетическая и светотехническая ( 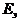и 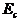) по формулам

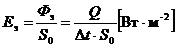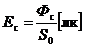; . (1.28)

Освещенность ИВС легко может быть измерена и тем самым на основании (1.25, 1.27 и 1.28) определено соответствующее число фотонов, падающих на ИВС. Действительно, для монохроматического излучения

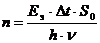(1.29)

и тогда соотношения (1.22 и 1.23) могут быть представлены в следующем виде:

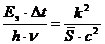. (1.30)

Полученные соотношения (1.30) позволяют получить жесткую функциональную зависимость между легко измеряемыми или конструктивно задаваемыми (как в устройствах считывания) размером элемента разложения ( 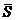), параметрами получения символа визуального сообщения ( 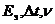) и предельно возможным при заданной допустимой погрешности (k) минимальным контрастом (c), практическое измерение которого трудно выполнимо.

Выразив из (1.30) c - предельно возможный минимальный контраст и подставив его в (1.10), с учетом того, что 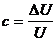и 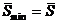, получим выражение для максимального предельного количества информации (H), которое может содержаться в символе ИВС единичной площади

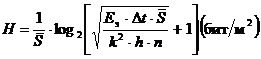(1.31)

или с учетом того, что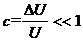

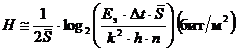. (1.32)

А максимальное предельное среднее количество информации, приходящееся на один элемент разложения, определяется соотношением

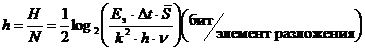. (1.33)

Именно выражения 1.33 и 1.34 могут служить численной мерой качества изображения, потому что предельная энтропия (H) и предельное среднее количество информации, приходящейся на один элемент разложения (h) изображения характеризуют изображения с основополагающей информационной точки зрения, которая во многом определяет их потребительские свойства. Достоинством предложенного метода определения качества изображения является и то, что практическое использование соотношений 1.33 и 1.34 не вызывает трудностей, так как все входящие в них величины могут быть либо легко измерены, либо заданы конструктивно. В качестве примера определим предлагаемым способом качество изображения, которое может быть получено в процессе считывания фотоизображения размером 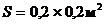при освещении его равномерным световым потоком 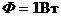, генерируемым гелий-неоновым лазером с длиной волны 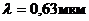( 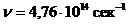). Считывание производится квадратной аппертурой с линейным размером d (мкм) ( 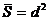) с быстродействием 10⁵ элементов/сек ( 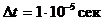) и вероятность ложного измерения различимых уровней контраста не превышающей 0,01% (k=4). В этом случае исходя из выше приведенных соотношений легко найти:

- число различимых уровней контраста (m):

;

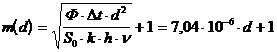- среднее количество информации, приходящейся на один элемент разложения h(d):

;

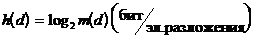- предельное количество информации, содержащейся на всем изображении I(d):

;

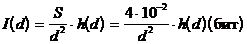- предельная энтропия изображения H(d) при :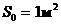

.

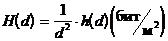В табл.1.2 приведены значения 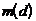, , 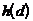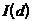и 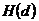при различных значениях d.

Табл.1.2

d(10-6м)
ΔS(10-12м)
m
h(бит/эл.разл.)	3,0	5,2	6,2	6,7	7,5
I(бит)	1,2·1011	8,3·109	2,5·109	1,2·109	4,8·108
H(бит/м2)	3,0·1012	2,1·1011	6,2·1010	3,0·1010	1,2·1010
H(бит/мм2)	3,0·106	2,1·105	6,2·104	3,0·104	1,2·104

Важно так же отметить, что в случае регистрации изображений с помощью реальных регистрирующих устройств в регистрирующее устройство попадает лишь часть ( 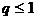) фотонов, отраженных символом визуального сообщения, но и эти попадающие в регистрирующее устройство фотоны регистрируются не все, так как квантовый выход регистрирующих устройств ( 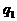), как правило, меньше 1.

Поэтому в этом случае для регистрации изображения символа визуального сообщения с заданным качеством необходимо корректировать полученные соотношения, еще больше увеличивая общее число фотонов, падающих на символ визуального сообщения ( ):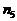

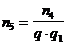. (1.34)

Все выкладки, приведенные выше, касались прежде всего излучения в видимой области спектра (0,4 - 0,7 мкм), однако, так как исходными предпосылками при выводе соотношений является исключительно квантовая теория, то очевидно, что все вышесказанное справедливо и к системам, работающим во всем диапазоне электромагнитного излучения.

Следует также учитывать, что полученные соотношения справедливы только при условии, что линейные размеры элемента разложения значительно превышают длину волны светового излучения, падающего на ИВС, так как они не учитывают волновые эффекты света.

Такой способ определения качества изображения, с нашей точки зрения, является более корректным по сравнению с использованием для этих целей полос заданного контраста, потому что именно с помощью элементов разложения (а не полос) можно построить любое изображение, и современные автоматические методы обработки изображений предполагают разбиение изображения на совокупность элементов, форма которых близка к кругу или квадрату.

Предложенный подход к определению качества изображения хорошо согласуется с методологией современных физических представлений, которые запрещают обсуждать явления сами по себе, независимо от способа их наблюдения. При этом различные явления относятся к объективной реальности (не зависящей от сознания субъекта), а их наблюдение позволяет получить физическую реальность, то есть ту часть объективной реальности, которая может быть познана опытным путем и сознанием субъекта, причем величина этой части зависит от способа наблюдения.

Поэтому очевидно, что качество изображения (его информативность) как физическая реальность, отражающая некую часть объективной реальности, будет определяться условиями наблюдения - степенью освещенности изучаемого объекта.