Умножение изображений. Свертка функций
Сверткой функций  и и  (обозначается (обозначается  ) называется интеграл ) называется интеграл 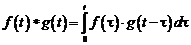 . . |
Несложно убедиться, что записанный интеграл не меняет своего значения от перестановки функций f и g, т.е.
 ,
,
или
 .
.
Теорема свертывания оригиналов. Если  и и  , то , то  , т.е. изображение свертки двух оригиналов равно произведению их изображений. , т.е. изображение свертки двух оригиналов равно произведению их изображений. |
На основании теоремы свертывания легко находится изображение интеграла от данной функции, если известно изображение самой функции: если  , то
, то  .
.
Пример. Найти свертку функций  и
и  и ее изображение.
и ее изображение.
Решение. По определению свертки
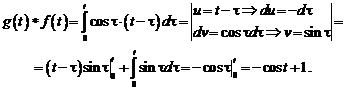
Найдем изображение свертки:
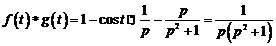 .
.
На основании теоремы свертывания изображение можно найти иначе. Так как 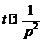 ,
,  , то
, то
 .
.
Теорема об интегрировании изображения
Если  и интеграл и интеграл 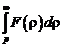 сходится, то сходится, то 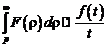 , т.е. интегрированию изображения соответствует деление его оригинала на t. , т.е. интегрированию изображения соответствует деление его оригинала на t. |
Пример. Найти изображение функций 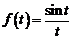 и
и 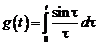 .
.
Решение. Так как  , то, учитывая сформулированную теорему,
, то, учитывая сформулированную теорему,
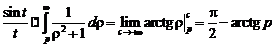 .
.
Найдем изображение для функции  , используя свойство интегрирования оригинала:
, используя свойство интегрирования оригинала:
 .
.
Дифференцирование оригинала
Если  и функции и функции 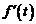 , ,  ,…, ,…,  являются оригиналами, то являются оригиналами, то  , ,  , …………………………… , ……………………………  . . |
Таблица некоторых изображений
Для удобства использования полученных выше изображений поместим их в одну таблицу.
| № | Оригинал  | Изображение  . . |
| С |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  |
Кроме того, рассмотренные выше свойства преобразований Лапласа представляют собой основные правила операционного исчисления. Для удобства использования перечислим их еще раз.
1.Линейность:  .
.
2.Подобие:  .
.
3.Смещение изображения:  .
.
4.Дифференцирование изображения:  .
.
5.Запаздывание оригинала:  .
.
6.Умножение изображений:  .
.
7.Интегрирование оригинала:  .
.
8.Интегрирование изображения:  .
.
9.Дифференцирование оригинала:
 ,
,
 ,
,
……………………………
 .
.
Примеры.
1. Найти изображения функций:
а)  ;
;
б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
Решение.
а) По таблице находим:
 .
.
Следовательно, по свойству линейности преобразования Лапласа получим

б) Преобразуем произведение косинусов в их сумму
 ,
,
т.е.
 .
.
Далее воспользуемся таблицей изображений и свойством линейности:
 .
.
в) Используем формулу понижения степени:
 .
.
Поэтому  . Тогда
. Тогда
 .
.
г) Раскроем скобки  . Для того, чтобы найти изображение первого слагаемого воспользуемся теоремой о дифференцировании изображения. Так как
. Для того, чтобы найти изображение первого слагаемого воспользуемся теоремой о дифференцировании изображения. Так как  , то
, то
 .
.
Окончательно,
 .
.
д) Для того, чтобы найти изображение первого слагаемого, используем теорему о дифференцировании изображения:
 .
.
Преобразуем второе слагаемое:
 .
.
Поэтому его изображение имеет вид
 .
.
Итак, изображение заданной функции будет
 .
.
2. Найти оригиналы следующих изображений:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  .
.
Решение.
а) Преобразуем 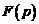 так, чтобы можно было воспользоваться таблицей изображений:
так, чтобы можно было воспользоваться таблицей изображений:

Находя по таблице оригинал каждого слагаемого и используя свойство линейности, получим начальную функцию для заданного изображения.
 .
.
б) Преобразуем дробь, выделив полный квадрат в знаменателе:
 .
.
Сведем полученное выражение к сумме двух дробей, соответствующих формулам 7 и 8 таблицы изображений.
 .
.
Следовательно, согласно таблице изображений и свойству линейности преобразования Лапласа, находим оригинал:
 .
.
в) Разложив знаменатель дроби на множители, перепишем изображение в виде:
 .
.
Представим полученную дробь в виде суммы простейших дробей и найдем входящие в сумму коэффициенты.


Таким образом  . Теперь по таблице изображений находим
. Теперь по таблице изображений находим
 .
.
г) Представим дробь в виде суммы простейших дробей
 .
.
Приводя правую часть равенства к общему знаменателю и приравнивая числители обеих дробей, получаем равенство:
 .
.
Отсюда при  сразу находим
сразу находим  . Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты.
. Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты.

Таки образом,
 .
.
Следовательно,
 .
.
д) Разложим дробь в сумму простейших дробей
 .
.
Приведем правую часть равенства к общему знаменателю и приравняем числители обеих дробей
 .
.
При  получаем
получаем  . Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты
. Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты

Итак,
 .
.
Следовательно,
 .
.
е) Представим заданное изображение в виде произведения двух функций и воспользуемся теоремой об умножении изображений.
 .
.
Так как  и
и  , то
, то

Итак,  .
.
ж) Используем теорему запаздывания. Так как  и
и  , то
, то
 .
.
Таким образом,

