Глава 5. элементы операционного исчисления
Глава 5. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
5.1. Основные определения
Основными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть задана функция  действительного переменного t. Функция действительного переменного t. Функция  называется оригиналом или начальной функцией, если она удовлетворяет следующим условиям: 1. называется оригиналом или начальной функцией, если она удовлетворяет следующим условиям: 1.  при при  . 2. . 2.  – кусочно-непрерывна при – кусочно-непрерывна при  , т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число. 3. Существуют такие числа , т.е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке таких точек лишь конечное число. 3. Существуют такие числа  и и  , что при всех t выполняется неравенство , что при всех t выполняется неравенство  , т.е. с ростом t функция , т.е. с ростом t функция  может возрастать не быстрее некоторой показательной функции. Число может возрастать не быстрее некоторой показательной функции. Число  называется показателем роста функции называется показателем роста функции  . . |
Заметим, что функция  может быть и комплексной функцией действительного переменного, т.е. иметь вид
может быть и комплексной функцией действительного переменного, т.е. иметь вид  ; она считается оригиналом, если действительные функции
; она считается оригиналом, если действительные функции  и
и  являются оригиналами.
являются оригиналами.
Пусть  – оригинал, а
– оригинал, а  – комплексный параметр, причем
– комплексный параметр, причем  . Рассмотрим произведение функции
. Рассмотрим произведение функции  на комплексную функцию
на комплексную функцию  действительного переменного t:
действительного переменного t:  и определим несобственный интеграл
и определим несобственный интеграл
 .
.
Можно показать, что при сформулированных условиях этот интеграл сходится и является функцией переменного р:
 . . |
Этот интеграл называется интегралом Лапласа, а определяемая им функция  – преобразованием Лапласа, или лапласовым изображением
– преобразованием Лапласа, или лапласовым изображением  , или просто изображением
, или просто изображением  . Соответствие между оригиналом
. Соответствие между оригиналом  и его изображением
и его изображением  будем записывать в виде
будем записывать в виде
 или
или  .
.
Теорема (о единственности оригинала). Если две непрерывные функции  и
и  имеют одно и то же изображение
имеют одно и то же изображение  , то эти функции совпадают.
, то эти функции совпадают.
Примеры.
 1. По определению найдем изображение единичной функции Хевисайда, определяемой следующим образом
1. По определению найдем изображение единичной функции Хевисайда, определяемой следующим образом

График введенной функции изображен на рисунке.
Решение.


Итак,  .
.
2. Найти изображение функции  , где а – любое число.
, где а – любое число.
Решение. Данная функция является оригиналом. По определению изображения имеем

если  . Таким образом,
. Таким образом,  .
.
3.  Найти изображение функции, заданной на рисунке.
Найти изображение функции, заданной на рисунке.
Решение. Зададим функцию аналитически

и воспользуемся определением.


4. Найти изображение функции


Решение. График заданной функции изображен на рисунке. Чтобы найти изображение функции, воспользуемся определением.

5.2. Свойства преобразования Лапласа
Находить изображение, используя только определение, не всегда просто. Свойства преобразования Лапласа облегчают задачу нахождения изображений для большого числа функций, а также задачу отыскания оригиналов по их изображениям.
Линейность изображения
Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные, т.е. если  и и  , то , то  , где , где  и и  – постоянные. – постоянные. |
Используя сформулированное свойство и выведенные соответствия 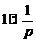 ,
,  , найдем изображения функций: С,
, найдем изображения функций: С,  ,
,  ,
,  ,
,  .
.
1)  .
.
2) 
 .
.
Таким образом,  .
.
3) Аналогично, учитывая формулу  , можно доказать соответствие
, можно доказать соответствие  .
.
4) Используя определение гиперболического синуса  и свойство линейности изображения, несложно получить соответствие
и свойство линейности изображения, несложно получить соответствие  .
.
5) Аналогично из определения гиперболического косинуса  следует формула
следует формула  .
.
Свойство подобия
Если  и λ – произвольная положительная постоянная, то и λ – произвольная положительная постоянная, то  , т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число. , т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число. |
Теорема смещения
Если  и и  , то , то  , т.е. при умножении оригинала на функцию , т.е. при умножении оригинала на функцию  аргумент изображения смещается на величину а. аргумент изображения смещается на величину а. |
Используя это свойство и найденные выше изображения, легко получить следующие соотношения
 ,
,
 .
.
Теорема запаздывания
Пусть функция  – оригинал. Тогда график функции
– оригинал. Тогда график функции  имеет тот же вид, но смещен на
имеет тот же вид, но смещен на  единиц вправо (при
единиц вправо (при  ). Следовательно, функции
). Следовательно, функции  и
и  описывают один и тот же процесс, но процесс, описываемый функцией
описывают один и тот же процесс, но процесс, описываемый функцией  , начинается с опозданием на время
, начинается с опозданием на время  .
.
 |
Справедлива следующая теорема.
Теорема. Если  , ,  , то , то  , т.е. запаздывание оригинала на положительную величину , т.е. запаздывание оригинала на положительную величину  приводит к умножению изображения оригинала на приводит к умножению изображения оригинала на  . . |
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями.
 Найдем изображение функции
Найдем изображение функции  . Эта функция получается из единичной функции Хевисайда
. Эта функция получается из единичной функции Хевисайда  смещением на
смещением на  единиц. Ее график изображен на рисунке. Так как
единиц. Ее график изображен на рисунке. Так как  , то по теореме запаздывания
, то по теореме запаздывания  .
.
Примеры.
1. Найти изображение функции

 Решение. График функции изображен на рисунке. Заданную функцию можно описать с помощью единичной функции Хевисайда следующим образом:
Решение. График функции изображен на рисунке. Заданную функцию можно описать с помощью единичной функции Хевисайда следующим образом:
 .
.
Поэтому по теореме запаздывания
 .
.
Заметим, что ранее это изображение было найдено по определению.
 |
2. Найти изображение функции, заданной на рисунке.
Решение. Зададим функцию  аналитически.
аналитически.

или  . Следовательно, изображение заданной функции имеет вид
. Следовательно, изображение заданной функции имеет вид
 .
.
3. Найти изображение функции

 Решение. График функции построен на рисунке. Заметим, что заданную функцию можно так же описать с помощью единичной функции Хевисайда следующим образом:
Решение. График функции построен на рисунке. Заметим, что заданную функцию можно так же описать с помощью единичной функции Хевисайда следующим образом:
 .
.
Так как по теореме запаздывания справедливо соотношение
 ,
,
то по теореме смещения окончательно получаем
 .
.
Ранее изображение этой функции было найдено исходя из определения.
4. Найти изображение функции


Решение. Функция-оригинал изображена на рисунке. Запишем ее, используя функцию Хевисайда.

Преобразуем полученное выражение:

Раскроем скобки и приведем подобные слагаемые:
 .
.
По теореме запаздывания найдем изображение заданной функции.
 .
.
5. Найти оригинал для изображения  .
.
Решение. Так как  , то воспользуемся теоремой запаздывания:
, то воспользуемся теоремой запаздывания:
 ,
,
или

Дифференцирование оригинала
Если  и функции и функции 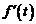 , ,  ,…, ,…,  являются оригиналами, то являются оригиналами, то  , ,  , …………………………… , ……………………………  . . |
Таблица некоторых изображений
Для удобства использования полученных выше изображений поместим их в одну таблицу.
| № | Оригинал  | Изображение  . . |
| С |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  | |
 |  |
Кроме того, рассмотренные выше свойства преобразований Лапласа представляют собой основные правила операционного исчисления. Для удобства использования перечислим их еще раз.
1.Линейность:  .
.
2.Подобие:  .
.
3.Смещение изображения:  .
.
4.Дифференцирование изображения:  .
.
5.Запаздывание оригинала:  .
.
6.Умножение изображений:  .
.
7.Интегрирование оригинала:  .
.
8.Интегрирование изображения:  .
.
9.Дифференцирование оригинала:
 ,
,
 ,
,
……………………………
 .
.
Примеры.
1. Найти изображения функций:
а)  ;
;
б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
Решение.
а) По таблице находим:
 .
.
Следовательно, по свойству линейности преобразования Лапласа получим

б) Преобразуем произведение косинусов в их сумму
 ,
,
т.е.
 .
.
Далее воспользуемся таблицей изображений и свойством линейности:
 .
.
в) Используем формулу понижения степени:
 .
.
Поэтому  . Тогда
. Тогда
 .
.
г) Раскроем скобки  . Для того, чтобы найти изображение первого слагаемого воспользуемся теоремой о дифференцировании изображения. Так как
. Для того, чтобы найти изображение первого слагаемого воспользуемся теоремой о дифференцировании изображения. Так как  , то
, то
 .
.
Окончательно,
 .
.
д) Для того, чтобы найти изображение первого слагаемого, используем теорему о дифференцировании изображения:
 .
.
Преобразуем второе слагаемое:
 .
.
Поэтому его изображение имеет вид
 .
.
Итак, изображение заданной функции будет
 .
.
2. Найти оригиналы следующих изображений:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  .
.
Решение.
а) Преобразуем 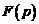 так, чтобы можно было воспользоваться таблицей изображений:
так, чтобы можно было воспользоваться таблицей изображений:

Находя по таблице оригинал каждого слагаемого и используя свойство линейности, получим начальную функцию для заданного изображения.
 .
.
б) Преобразуем дробь, выделив полный квадрат в знаменателе:
 .
.
Сведем полученное выражение к сумме двух дробей, соответствующих формулам 7 и 8 таблицы изображений.
 .
.
Следовательно, согласно таблице изображений и свойству линейности преобразования Лапласа, находим оригинал:
 .
.
в) Разложив знаменатель дроби на множители, перепишем изображение в виде:
 .
.
Представим полученную дробь в виде суммы простейших дробей и найдем входящие в сумму коэффициенты.


Таким образом  . Теперь по таблице изображений находим
. Теперь по таблице изображений находим
 .
.
г) Представим дробь в виде суммы простейших дробей
 .
.
Приводя правую часть равенства к общему знаменателю и приравнивая числители обеих дробей, получаем равенство:
 .
.
Отсюда при  сразу находим
сразу находим  . Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты.
. Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты.

Таки образом,
 .
.
Следовательно,
 .
.
д) Разложим дробь в сумму простейших дробей
 .
.
Приведем правую часть равенства к общему знаменателю и приравняем числители обеих дробей
 .
.
При  получаем
получаем  . Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты
. Далее, раскрывая скобки в правой части равенства и приравнивая коэффициенты при одинаковых степенях р, найдем остальные коэффициенты

Итак,
 .
.
Следовательно,
 .
.
е) Представим заданное изображение в виде произведения двух функций и воспользуемся теоремой об умножении изображений.
 .
.
Так как  и
и  , то
, то

Итак,  .
.
ж) Используем теорему запаздывания. Так как  и
и  , то
, то
 .
.
Таким образом,

Примеры.
1. Используя операционное исчисление, найти частное решение дифференциального уравнения 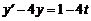 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 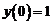 .
.
Решение. Пусть 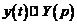 , тогда
, тогда 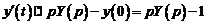 , кроме того
, кроме того 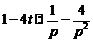 . Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению
. Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению
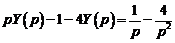 .
.
Выразим из полученного уравнения функцию 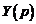 :
:
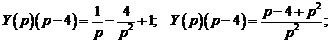
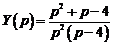 .
.
Представим эту рациональную дробь как сумму простейших дробей:
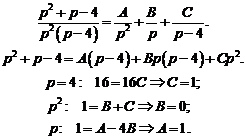
Итак, 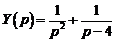 . Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения:
. Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения:
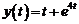 .
.
2. Найти частное решение дифференциального уравнения 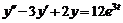 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 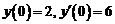 .
.
Решение. Пусть 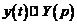 . Тогда
. Тогда
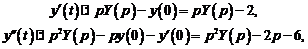
и 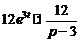 .
.
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
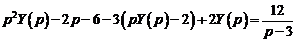 ,
,
или
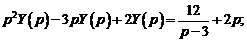
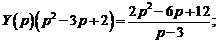
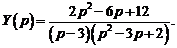
Методом неопределенных коэффициентов найдем разложение этой дроби в сумму простейших дробей.
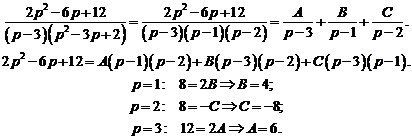 Таким образом,
Таким образом, 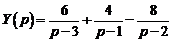 . Следовательно, частное решение данного дифференциального уравнения будет
. Следовательно, частное решение данного дифференциального уравнения будет
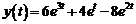 .
.
 3. Решить задачу Коши
3. Решить задачу Коши 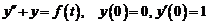 , где функция
, где функция  задана графически на рисунке.
задана графически на рисунке.
Решение. Пусть 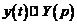 . Тогда
. Тогда 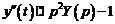 . Найдем изображение функции
. Найдем изображение функции  , воспользовавшись теоремой запаздывания. Зададим
, воспользовавшись теоремой запаздывания. Зададим  аналитически, используя единичную функцию Хевисайда:
аналитически, используя единичную функцию Хевисайда:
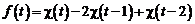 .
.
Тогда
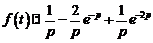 .
.
Операторное уравнение принимает вид
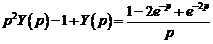 .
.
Находим из него неизвестное изображение 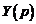 :
:
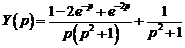 .
.
Разложим дробь 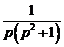 в сумму простейших дробей.
в сумму простейших дробей.
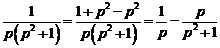 .
.
(При разложении можно использовать метод неопределенных коэффициентов.) Следовательно,
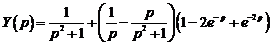 .
.
Еще раз используя теорему запаздывания, найдем искомое решение дифференциального уравнения:
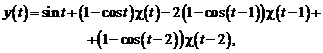
или
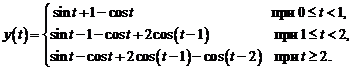
4.Операционным методом решить систему линейных дифференциальных уравнений
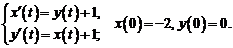
Решение. Пусть 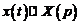 ,
, 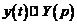 . Тогда
. Тогда 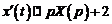 ,
, 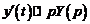 и
и 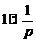 . Система операторных уравнений принимает вид
. Система операторных уравнений принимает вид
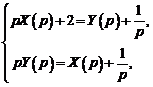 или
или 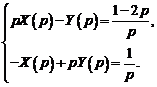
Получили систему линейных алгебраических уравнений относительно изображений 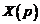 и
и 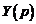 . Для ее решения используем метод Крамера.
. Для ее решения используем метод Крамера.
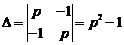 ,
,
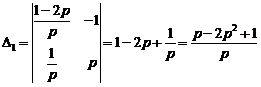 ,
,
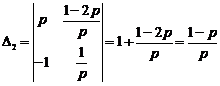 .
.
Итак,
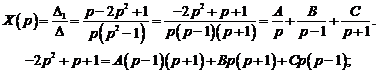
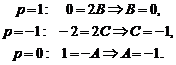
Тогда 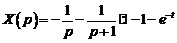 .
.
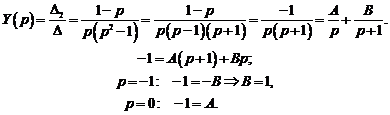
Следовательно, 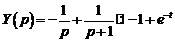 .
.
Таким образом, решением системы дифференциальных уравнений, удовлетворяющим заданным начальным условиям являются функции 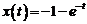 ,
, 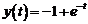 .
.
5.Операционным методом решить систему линейных дифференциальных уравнений
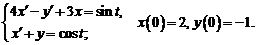
Решение. Перейдем к изображениям искомых функций:
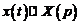 ,
, 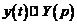 ,
,
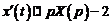 ,
, 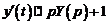 .
.
Кроме того,
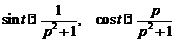 .
.
Тогда система операторных уравнений будет иметь вид
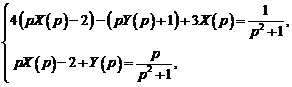
или
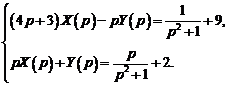
Решим полученную систему методом Крамера.
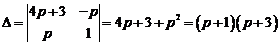 ,
,
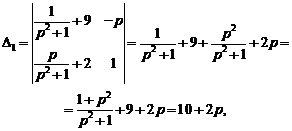
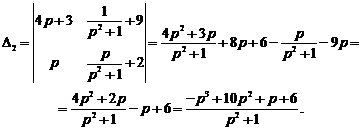
Выпишем изображения искомых функций:
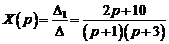 ,
,
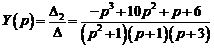 .
.
Используя метод неопределенных коэффициентов, восстановим оригиналы.
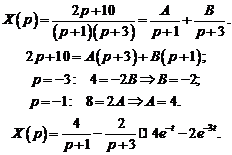
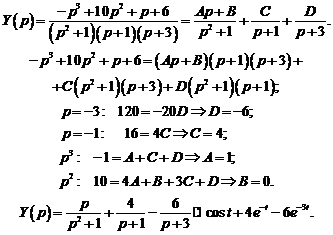
Таким образом, решением системы уравнений являются функции 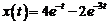 ,
, 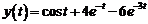 .
.
Задачи для практических занятий и самостоятельной работы по теме Операционное исчисление»
1.Найдите изображения следующих функций:
1) 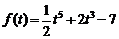 .Ответ:
.Ответ: 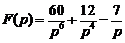 .
.
2) 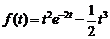 .Ответ:
.Ответ: 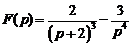 .
.
3) 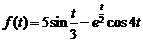 .
.
Ответ: 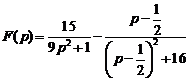 .
.
4) 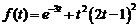 .Ответ:
.Ответ: 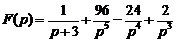 .
.
5) 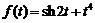 . Ответ:
. Ответ: 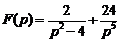 .
.
6) 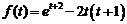 .Ответ:
.Ответ: 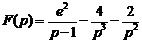 .
.
7) 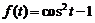 . Ответ:
. Ответ: 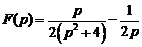 .
.
8) 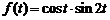 .Ответ:
.Ответ: 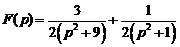 .
.
9) 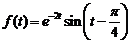 .
.
Ответ: 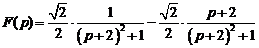 .
.
10) 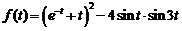 .
.
Ответ: 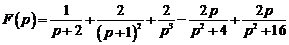 .
.
11) 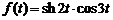 .
.
Ответ: 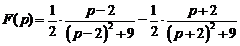 .
.
12) 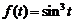 .Ответ:
.Ответ: 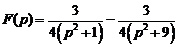 .
.
13) 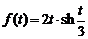 .Ответ:
.Ответ: 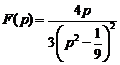 .
.
14) 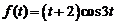 . Ответ:
. Ответ: 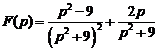 .
.
15) 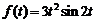 .Ответ:
.Ответ: 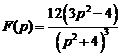 .
.
16) 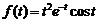 .Ответ:
.Ответ: 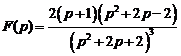 .
.
2.Найдите оригиналы по заданным изображениям:
1) 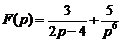 . Ответ:
. Ответ: 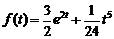 .
.
2) 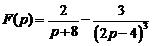 . Ответ:
. Ответ: 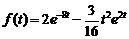 .
.
3) 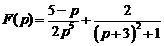 .
.
Ответ: 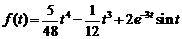 .
.
4) 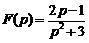 . Ответ:
. Ответ: 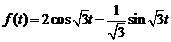 .
.
5) 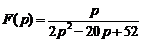 . Ответ:
. Ответ: 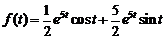 .
.
6) 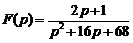 .
.
Ответ: 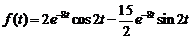 .
.
7) 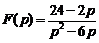 . Ответ:
. Ответ: 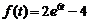 .
.
8) 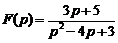 . Ответ:
. Ответ: 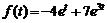 .
.
9) 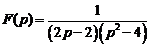 . Ответ:
. Ответ: 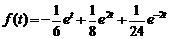 .
.
10) 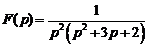 . Ответ:
. Ответ: 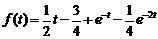 .
.
11) 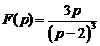 . Ответ:
. Ответ: 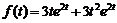 .
.
12) 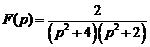 .
.
Ответ: 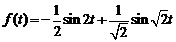 .
.
13) 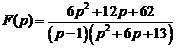 .
.
Ответ: 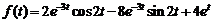 .
.
14) 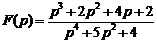 . Ответ:
. Ответ: 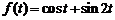 .
.
15) 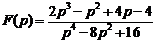 .
.
Ответ: 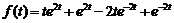 .
.
16) 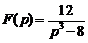 . Ответ:
. Ответ: 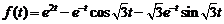 .
.
3.Найдите свертку функций и ее изображение:
1) 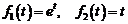 .
.
Ответ: 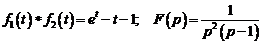 .
.
2) 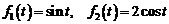 .
.
Ответ: 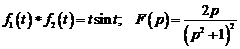 .
.
3) 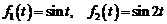 .
.
Ответ: 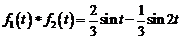 ;
;
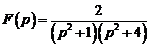 .
.
4) 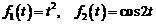 .
.
Ответ: 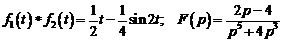 .
.
5) 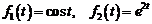 .
.
Ответ: 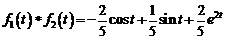 ;
;
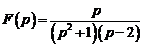 .
.
4.Найдите оригиналы для следующих изображений, используя теорему свертывания:
1) 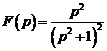 . Ответ:
. Ответ:  .
.
2) 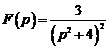 . Ответ:
. Ответ: 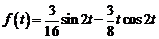 .
.
3) 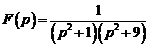 . Ответ:
. Ответ: 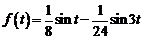 .
.
4) 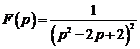 . Ответ:
. Ответ: 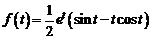 .
.
5.Используя теорему запаздывания, найдите изображения следующих функций:
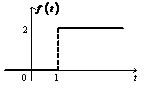 1)
1)
 Ответ:
Ответ: 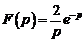 .
.
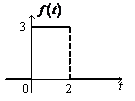 2)
2)
 Ответ:
Ответ: 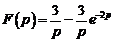 .
.
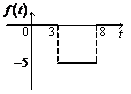
3)
Ответ: 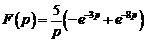 .
.
4) 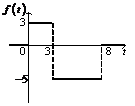
 Ответ:
Ответ: 
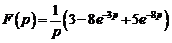 .
.
5) 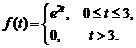 Ответ:
Ответ: 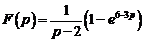 .
.
6) 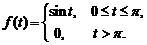
Ответ: 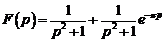 .
.
6.Используя теорему запаздывания, найдите оригиналы для следующих изображений:
1) 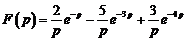 . Ответ:
. Ответ: 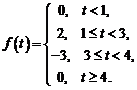
2) 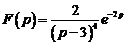 . Ответ:
. Ответ: 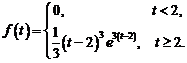
3) 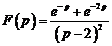 .
.
Ответ: 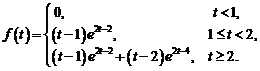
4) 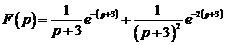 .
.
Ответ: 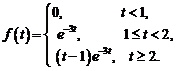
7.Решите дифференциальные уравнения операционным методом:
1) 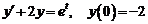 . Ответ:
. Ответ: 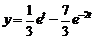 .
.
2) 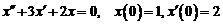 . Ответ:
. Ответ: 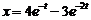 .
.
3) 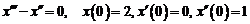 . Ответ:
. Ответ: 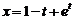 .
.
4) 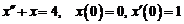 . Ответ:
. Ответ: 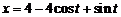 .
.
5) 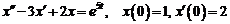 .
.
Ответ: 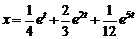 .
.
6) 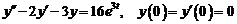 .
.
Ответ: 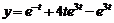 .
.
7) 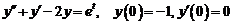 .
.
Ответ: 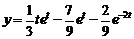 .
.
8) 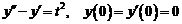 .
.
Ответ: 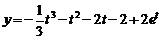 .
.
9) 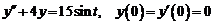 .
.
Ответ: 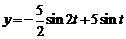 .
.
10) 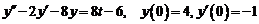 .
.
Ответ: 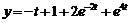 .
.
11) 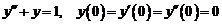 .
.
Ответ: 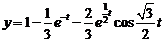 .
.
12) 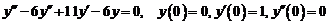 .
.
Ответ: 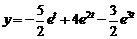 .
.
13) 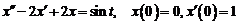 .
.
Ответ:
