Механизм корреляции изображений

Одной из важнейших частей программ по цифровой обработке является корреляционный алгоритм, позволяющий автоматически определять соответственные точки снимков с высокой точностью, многократно увеличивая производительность труда оператора при проведении ориентирования в процессе измерений и построении ЦМР.

Отметим, что попытки автоматизировать процесс поиска соответственных точек (заменить при стереоизмерениях человека машиной) предпринимались еще в первой трети 20 века [12]. После второй мировой войны появилась реальная возможность решения этой задачи, и вскоре были созданы первые автоматические стереосистемы для измерения параллаксов электронными методами. При электронном определении параллаксов имеют место следующие два основных процесса: преобразование фотографических плотностей в электрические сигналы (то есть сканирование) и сравнение этих сигналов в корреляторе. Основная задача коррелятора оценить степень подобия между сигналами, идущими от снимков стереопары.

Величина продольного параллакса определялась как произведение скорости синхронно движущихся вдоль снимков сканирующих элементов на величину задержки времени между появлением подобных сигналов на левом и правом снимках стереопары. Определялось это время путем анализа выходного сигнала коррелятора, который должен быть равен максимуму при максимальном соответствии точек на левом и правом снимках.

При обработке цифровых снимков используется статистический метод, при котором участок на одном снимке сравнивается с различными участками на другом снимке. Причем речь идет о дискретных величинах, так как изображение – это множество пикселов, каждому из которых соответствует число (x, например, на левом снимке, а y – на правом) являющееся функцией оптической плотности. Поэтому коэффициент корреляции K можно оценивать по известной формуле:

,

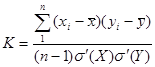(131)

где 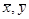- средние а s¢(X),s¢(Y) стандарты множеств X и Y тех числовых значений, которые принимают пикселы в сравниваемых окнах. Понятно, что решением является максимальное значение коэффициента корреляции. На этом принципе и основаны алгоритмы поиска соответственных точек в большинстве программных продуктов цифровых фотограмметрических систем. Для того, чтобы уменьшить зону поиска, как правило, предлагается две-три соответственные точки (иногда и больше) зафиксировать в ручную. Кроме того, следует отметить, что механизм работает тем лучше, чем менее монотонно изображение объекта на снимках пары. Поэтому оператору целесообразно контролировать качество работы коррелятора и вовремя вводить коррективы.

В некоторых алгоритмах (PHOTOMOD) используются локально-нормированные значения, плотности, что делает его нечувствительным к различным уровням яркости и контрастности левого и правого снимков и позволяет легко различить соответственные точки даже при работе с изображениями плохого качества. Алгоритм также позволяет изменять размеры корреляционного окна для достижения нужного компромисса между надежностью и точностью определения соответственных точек и использовать ряд других параметров настройки коррелятора. Использование эпиполярных снимков значительно ускоряет работу коррелятора, так как предполагается, что соответственные точки расположены на одних и тех же строках растров левого и правого снимков.

5.3.4 Внутреннее ориентирование снимка в системе координат цифрового изображения (Михайлов)

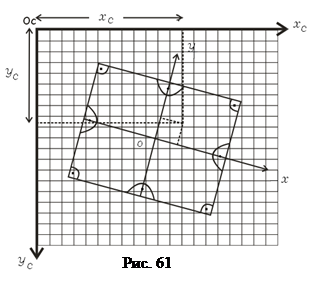
Процесс внутреннего ориентирования снимка производится для определения координат точек в системе координат снимка по значениям их координат в системе координат цифрового изображения. В результате определяются параметры, характеризующие положение и ориентацию системы координат снимка Sxyz в системе координат цифрового изображения o_cx_cy_c, а так же параметры, позволяющие исключить влияние систематической деформации фотоматериала, на котором был получен исходный аналоговый снимок (рис.61). Для определения параметров внутреннего ориентирования снимка измеряют координаты изображений координатных меток снимка в системе координат цифрового изображения.

Выбор метода определения параметров внутреннего ориентирования снимка зависит от методики фотограмметрической калибровки съемочной камеры. Если в процессе ее были определены координаты координатных меток в системе координат съемочной камеры (снимка) Sxyz, то для определения координат точек в системе координат снимка по значениям их координат в системе цифрового изображения используют формулы аффинного преобразования координат:

,

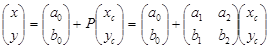(132)

которые можно представить и в развернутом виде:

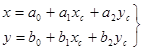(133)

Формулы (132) позволяют не только определить положение и ориентацию системы координат снимка в системе координат цифрового изображения, но и учесть систематические искажения снимка, возникающие из-за деформации фотопленки, на которой был получен снимок.

Параметры аффинного преобразования a_i, b_i можно определить по координатам x_c,y_c координатных меток снимка, измеренных на цифровом изображении, и значениям координат x,y этих меток в системе координат снимка, полученным при калибровке съемочной камеры.

Для определения параметров a_i,b_i для каждой метки, измеренной на цифровом изображении, составляют уравнения:

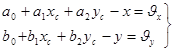(134)

Полученную систему уравнений решают по методу наименьших квадратов. При этом необходимо иметь не менее 3 координатных меток, не лежащих на одной прямой.

В практике фотограмметрии возникает задача определения значений координат точек в системе координат цифрового изображения по координатам этих точек, полученным в системе координат снимка. Такое преобразование координат выполняется по формулам:

.

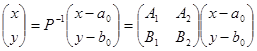(135)

Или

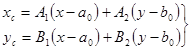(136)

В формулах (135) и (136) Ai, Bi – элементы обратной матрицы Р^-1.Значение пиксельных координат точек x_p,y_p определяют по формулам:

xp = xc/Δ, yp = yc/Δ

(137)

В случае, если при калибровке съемочной камеры определялись калиброванные расстояния между координатными метками l_x, l_y (рис.62), то для перехода от измеренных координат к координатам в системе координат снимка используют уравнения:

,

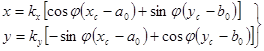(138)

в которых:

a_0, b₀ – координаты начала системы координат снимка в системе координат цифрового изображения;

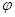- угол разворота оси х системы координат снимка относительно оси х_с системы координат цифрового изображения;

k_x, k_y – коэффициенты деформации снимка по осям x и y.

Если калиброванные расстояния между координатными меткамине известны, то формулы принимают вид:

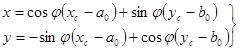(139)

Значения параметров j, a₀, b₀, k_x, k_y определяют по измеренным значениям координат координатных меток в системе координат цифрового изображения системы, а для оределения угла 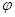используют соотношение:

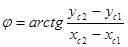(140)

в котором x_c1, y_c1 и x_c2, y_c2 – координаты 1 и 2 координатных меток в системе координат цифрового изображения.

	Рис.62

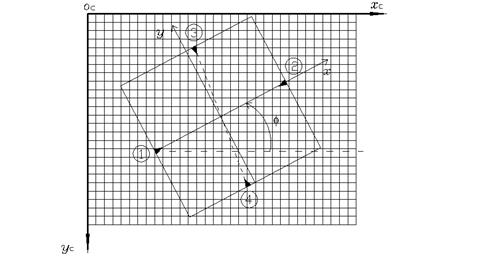
Значения коэффициентов k_x, k_y определяют по формулам:

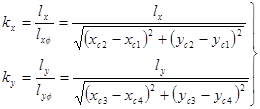(141)

где x_ci, y_ci – координаты координатных меток в системе координат цифрового изображения.

Параметры a₀, b₀ находят, как координаты x_c, y_c точки пересечения прямых линий, проведенных через координатные метки 1-2 и 3-4, при этом:

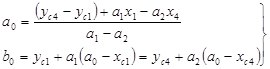(142)

В выше приведенных уравнениях:

a₁ = (y_c2 - y_c1)/(x_c2 - x_c1) и b₁ = (y_c3 - y_c4)/(x_c3 - x_c4).

Для определения координат точек снимка в системе координат цифрового изображения по координатам этих точек в системе координат снимка используют формулы:

,

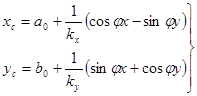(143)

в случае, если калиброванные расстояния l_x, l_y между координатными метками известны, и формулы:

,

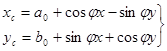(144)

если указанные расстояния не известны.

Необходимо заметить, что система координат цифрового изображения левая, поэтому в формулах 138 – 144 координата y_c берется с обратным знаком.

Определение пиксельных координат точек изображения производят по формулам (137).