Б. Ядерная модель атома Резерфорда

Обобщая результаты опытов по рассеянию α-частиц золотой фольгой, Резерфорд установил:

♦ атомы по своей природе в значительной мере прозрачны для α-частиц;

♦ отклонения α-частиц на большие углы возможны только в том случае, если внутри атома имеется очень сильное электрическое поле, создаваемое положительным зарядом, связанным с большой и сконцентрированной в очень малом объеме массой.

Для объяснения этих опытов Резерфорд предложил ядерную модель атома: в ядре атома (области с линейными размерами 10^-15-10^-14 м) сосредоточены весь его положительный заряд и практически вся масса атома (99,9 %). Вокруг ядра в области с линейными размерами ~10^-10 м (размеры атома оценены в молекулярно-кинетической теории) движутся по замкнутым орбитам отрицательно заряженные электроны, масса которых составляет лишь 0,1 % массы ядра. Следовательно, электроны находятся от ядра на расстоянии от 10 000 до 100 000 поперечников ядра, то есть основную часть атома составляет пустое пространство.

Ядерная модель атомов Резерфорда напоминает солнечную систему: в центре системы находится «солнце» – ядро, а вокруг него по орбитам движутся «планеты» – электроны, поэтому данную модель называют планетарной. Электроны не падают на ядро потому, что электрические силы притяжения между ядром и электронами уравновешиваются центробежными силами, обусловленными вращением электронов вокруг ядра.

В 1914 г., через три года после создания планетарной модели атома, Резерфорд исследовал положительные заряды в ядре. Бомбардируя электронами атомы водорода, он обнаружил, что нейтральные атомы превратились в положительно заряженные частицы. Так как атом водорода имеет один электрон, Резерфорд решил, что ядро атома является частицей, несущей элементарный положительный заряд +е. Эту частицу он назвал протоном.

Планетарная модель хорошо согласуется с опытами по рассеиванию α-частиц, но она не может объяснить устойчивость атома. Рассмотрим, например, модель атома водорода, содержащего ядро-протон и один электрон, который движется со скоростью v вокруг ядра по круговой орбите радиуса r. Электрон должен по спирали падать на ядро, и частота его обращения вокруг ядра (следовательно, и частота излучаемых им электромагнитных волн) должна непрерывно изменяться, то есть атом неустойчив, и его электромагнитное излучение должно иметь непрерывный спектр.

В действительности оказывается, что:

а) атом устойчив;

б) атом излучает энергию лишь при определенных условиях;

в) излучение атома имеет линейчатый спектр, определяемый его строением.

Таким образом, применение классической электродинамики к планетарной модели атома привело к полному противоречию с экспериментальными фактами. Преодоление возникших трудностей потребовало создания качественно новой – квантовой – теории атома. Однако, несмотря на свою несостоятельность, планетарная модель и сейчас принята в качестве приближенной и упрощенной картины атома.

2.6. Теория Бора для атома водорода. Постулаты Бора

Датский физик Нильс Бор (1885–1962) в 1913 г. создал первую квантовую теорию атома, связав в единое целое эмпирические закономерности линейчатых спектров водорода, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света.

В основу своей теории Бор положил три постулата, по поводу которых американский физик Л. Купер заметил: «Конечно, было несколько самонадеянно выдвигать предложения, противоречащие электродинамике Максвелла и механике Ньютона, но Бор был молод».

Первый постулат(постулат стационарных состояний): в атоме электроны могут двигаться только по определенным, так называемым разрешенным, или стационарным, круговым орбитам, на которых они, несмотря на наличие у них ускорения, не излучают электромагнитных волн (поэтому эти орбиты названы стационарными). Электрон на каждой стационарной орбите обладает определенной энергией E_n.

Второй постулат(правило частот): атом излучает или поглощает квант электромагнитной энергии при переходе электрона с одной стационарной орбиты на другую:

hv = E₁ – E₂,

где E₁ и E₂ – энергия электрона соответственно до и после перехода.

При E₁ > E₂ происходит излучение кванта (переход атома из одного состояния с большей энергией в состояние с меньшей энергией, то есть переход электрона с любой дальней на любую ближнюю от ядра орбиту); при E₁ < E₂ – поглощение кванта (переход атома в состояние с большей энергией, то есть переход электрона на более удаленную от ядра орбиту).

Будучи уверенным, что постоянная Планка должна играть основную роль в теории атома, Бор ввел третий постулат(правило квантования): на стационарных орбитах момент импульса электрона L_n= m_eυ_nr_n кратен величине = h/(2π), то есть

m_eυ_nr_n = nh, n = 1, 2, 3, …,

где = 1,05 · 10^-34 Дж · с – постоянная Планка (величина h/(2π)) встречается столь часто, что для нее введено специальное обозначение («аш» с чертой; в данной работе «аш»– прямое); m_е = 9,1 · 10^-31 кг – масса электрона; r_п – радиус n-й стационарной орбиты; υ_n – скорость электрона на этой орбите.

2.7. Атом водорода в квантовой механике

Уравнением движения микрочастицы в различных силовых полях является волновое уравнение Шредингера.

Для стационарных состояний уравнение Шредингера будет таким:

где Δ – оператор Лапласа

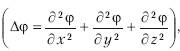
, m – масса частицы, h – постоянная Планка, E – полная энергия, U – потенциальная энергия.

Уравнение Шредингера является дифференциальным уравнением второго порядка и имеет решение, которое указывает на то, что в атоме водорода полная энергия должна иметь дискретный характер:

^E1^{, E}2^{, E}3…

Эта энергия находится на соответствующих уровнях n =1,2,3,…по формуле:

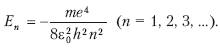
Самый нижний уровень E соответствует минимальной возможной энергии. Этот уровень называют основным, все остальные – возбужденными.

По мере роста главного квантового числа n энергетические уровни располагаются теснее, полная энергия уменьшается, и при n = ∞ она равна нулю. При E>0 электрон становится свободным, несвязанным с конкретным ядром, а атом – ионизированным.

Полное описание состояния электрона в атоме, помимо энергии, связано с четырьмя характеристиками, которые называются квантовыми числами. К ним относятся: главное квантовое число п, орбитальное квантовое число l, магнитное квантовое число m₁, магнитное спиновое квантовое число m_s.

Волновая φ-функция, описывающая движение электрона в атоме, представляет собой не одномерную, а пространственную волну, соответствующую трем степеням свободы электрона в пространстве, то есть волновая функция в пространстве характеризуется тремя системами. Каждая из них имеет свои квантовые числа: п, l, m_l.

Каждой микрочастице, в том числе и электрону, также свойственно собственное внутреннее сложное движение. Это движение может характеризоваться четвертым квантовым числом m_s. Поговорим об этом подробнее.

A.Главное квантовое число п, согласно формуле, определяет энергетические уровни электрона в атоме и может принимать значения п = 1, 2, 3…

Б.Орбитальное квантовое число /. Из решения уравнения Шредингера следует, что момент импульса электрона (его механический орбитальный момент) квантуется, то есть принимает дискретные значения, определяемые формулой

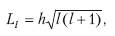
где L_l – момент импульса электрона на орбите, l – орбитальное квантовое число, которое при заданном п принимает значение i = 0, 1, 2… (n – 1) и определяет момент импульса электрона в атоме.

B.Магнитное квантовое число m_l. Из решения уравнения Шредингера следует также, что вектор L_l (момент импульса электрона) ориентируется в пространстве под влиянием внешнего магнитного поля. При этом вектор развернется так, что его проекция на направление внешнего магнитного поля будет

L_lz = hm_l

где m_l называется магнитным квантовым числом, которое может принимать значения m_l = 0, ±1, ±2,±1, то есть всего (2l + 1) значений.

Учитывая сказанное, можно сделать заключение о том, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях (n – одно и то же, а l и m_l– разные).

При движении электрона в атоме электрон заметно проявляет волновые свойства. Поэтому квантовая электроника вообще отказывается от классических представлений об электронных орбитах. Речь идет об определении вероятного места нахождения электрона на орбите, то есть местонахождение электрона может быть представлено условным «облаком». Электрон при своем движении как бы «размазан» по всему объему этого «облака». Квантовые числа n и l характеризуют размер и форму электронного «облака», а квантовое число m_l– ориентацию этого «облака» в пространстве.

В 1925 г. американские физики Уленбек и Гаудсмит доказали, что электрон также обладает собственным моментом импульса (спином), хотя мы не считаем электрон сложной микрочастицей. Позднее выяснилось, что спином обладают протоны, нейтроны, фотоны и другие элементарные частицы

Опыты Штерна, Герлаха и других физиков привели к необходимости характеризовать электрон (и микрочастицы вообще) добавочной внутренней степенью свободы. Отсюда для полного описания состояния электрона в атоме необходимо задавать четыре квантовых числа: главное – п, орбитальное – l, магнитное – m_l, магнитное спиновое число – m_s.

В квантовой физике установлено, что так называемая симметрия или асимметрия волновых функций определяется спином частицы. В зависимости от характера симметрии частиц все элементарные частицы и построенные из них атомы и молекулы делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются асимметричными волновыми функциями и подчиняются статистике Ферми—Дирака. Эти частицы называются фермионами. Частицы с целочисленным спином, в том числе и с нулевым, такие как фотон (Ls =1) или л-мезон (Ls = 0), описываются симметричными волновыми функциями и подчиняются статистике Бозе– Эйнштейна. Эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, также являются фермионами (суммарный спин – полуцелый), а составленные из четного – бозонами (суммарный спин – целочисленный).

2.8. Многоэлектронный атом. Принцип Паули

В многоэлектронном атоме, заряд которого равен Ze, электроны будут занимать различные «орбиты» (оболочки). При движении вокруг ядра Z-электроны располагаются в соответствии с квантово-механическим законом, который называется принципом Паули (1925 г.). Он формулируется так:

► 1. В любом атоме не может быть двух одинаковых электронов, определяемых набором четырех квантовых чисел: главного n, орбитального /, магнитного m и магнитного спинового m_s.

► 2. В состояниях с определенным значением могут находиться в атоме не более 2n² электронов.

Значит, на первой оболочке («орбите») могут находиться только 2 электрона, на второй – 8, на третьей – 18 и т. д.

Таким образом, совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны располагаются по подоболочкам, которые соответствуют определенному значению /. Так как орбитальное квантовое число l принимает значения от 0 до (п – 1), число подоболочек равно порядковому номеру оболочки п. Количество электронов в подоболочке определяется магнитным квантовым числом m_l и магнитным спиновым числом m_s.

Принцип Паули сыграл выдающуюся роль в развитии современной физики. Так, например, удалось теоретически обосновать периодическую систему элементов Менделеева. Без принципа Паули невозможно было бы создать квантовые статистики и современную теорию твердых тел.

2.9. Квантово-механическое обоснование Периодического закона Д. И. Менделеева

В 1869 г. Д. И. Менделеев открыл периодический закон изменения химических и физических свойств элементов в зависимости от их атомных масс. Д. И. Менделеев ввел понятие порядкового номера Z-элемента и, расположив химические элементы в порядке возрастания их номера, получил полную периодичность в изменении химических свойств элементов. Физический смысл порядкового номера Z-элемента в периодической системе был установлен в ядерной модели атома Резерфорда: Z совпадает с числом положительных элементарных зарядов в ядре (протонов) и, соответственно, с числом электронов в оболочках атомов.

Принцип Паули дает объяснение Периодической системы Д. И. Менделеева. Начнем с атома водорода, имеющего один электрон и один протон. Каждый последующий атом будем получать, увеличивая заряд ядра предыдущего атома на единицу (один протон) и добавляя один электрон, который мы будем помещать в доступное ему, согласно принципу Паули, состояние.

У атома водорода Z = 1 на оболочке 1 электрон. Этот электрон находится на первой оболочке (K-оболочка) и имеет состояние 1S, то есть у него n =1,а l =0(S-состояние), m = 0, m_s = ±l/2 (ориентация его спина произвольна).

У атома гелия (Не) Z = 2, на оболочке 2 электрона, оба они располагаются на первой оболочке и имеют состояние 1S, но с антипараллельной ориентацией спинов. На атоме гелия заканчивается заполнение первой оболочки (K-оболочки), что соответствует завершению I периода Периодической системы элементов Д. И. Менделеева. По принципу Паули, на первой оболочке больше 2 электронов разместить нельзя.

У атома лития (Li) Z = 3, на оболочках 3 электрона:2—на первой оболочке (К-оболочке)и1—на второй (L-оболочке). На первой оболочке электроны в состоянии 1S, а на второй – 2S. Литием начинается II периодтаблицы.

У атома бериллия (Be) Z = 4, на оболочках 4 электрона: 2 на первой оболочке в состоянии IS и 2 на второй в состоянии 2S.

У следующих шести элементов – от В (Z = 5) до Ne(Z = 10) – идет заполнение второй оболочки, при этом электроны находятся как в состоянии 2S, так и в состоянии 2р (у второй оболочки образуется 2 под-оболочки).

У атома натрия (Na) Z = 11. У него первая и вторая оболочки, согласно принципу Паули, полностью заполнены (2 электрона на первой и 8 электронов на второй оболочках). Поэтому одиннадцатый электрон располагается на третьей оболочке (М-оболочке), занимая наинизшее состояние 3S. Натрием открывается III период Периодической системы Д. И. Менделеева. Рассуждая подобным образом, можно построить всю таблицу.

Таким образом, периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов. Так, инертные газы имеют одинаковые внешние оболочки из 8 электронов.

2.10. Основные понятия ядерной физики

Ядра всех атомов можно разделить на два больших класса: стабильные и радиоактивные. Последние самопроизвольно распадаются, превращаясь в ядра других элементов. Ядерные преобразования могут происходить и со стабильными ядрами при их взаимодействии друг с другом и с различными микрочастицами.

Любое ядро заряжено положительно, и величина заряда определяется количеством протонов в ядре Z (зарядовое число). Количество протонов и нейтронов в ядре определяет массовое число ядра A. Символически ядро записывается так:

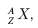
где X – символ химического элемента. Ядра с одинаковыми зарядовым числом Z и разными массовыми числами A называются изотопами. Например, уран в природе встречается в основном в виде двух изотопов

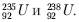
Изотопы обладают одинаковыми химическими свойствами и разными физическими. Например, изотоп урана ²³⁵₉₂U хорошо взаимодействуют с нейтроном ¹₀n любых энергий и может разделиться на два более легких ядра. В то же время изотоп урана ²³⁸₉₂U делится только при взаимодействии с нейтронами высоких энергий, более 1 мегаэлектроновольта (МэВ) (1 МэВ = 1,6 · 10^-13 Дж). Ядра с одинаковыми A и разными Z называются изобарами.

В то время как заряд ядра равен сумме зарядов входящих в него протонов, масса ядра не равна сумме масс отдельных свободных протонов и нейтронов (нуклонов), она несколько меньше ее. Это объясняется тем, что для связи нуклонов в ядре (для организации сильного взаимодействия) требуется энергия связи E. Каждый нуклон (и протон и нейтрон), попадая в ядро, образно говоря, выделяет часть своей массы для формирования внутриядерного сильного взаимодействия, которое «склеивает» нуклоны в ядре. При этом, согласно теории относительности (см. главу 3), между энергией E и массой m существует соотношение E = mc²,где с – скорость света в вакууме. Так что формирование энергии связи нуклонов в ядре E_св приводит к уменьшению массы ядра на так называемый дефект массы Δm = E_св · c². Эти представления подтверждены многочисленными экспериментами. Построив зависимость энергии связи на один нуклон E _св/ A = ε от числа нуклонов в ядре A, мы сразу увидим нелинейный характер этой зависимости. Удельная энергия связи ε с ростом A сначала круто возрастает (у легких ядер), затем характеристика приближается к горизонтальной (у средних ядер), а далее медленно снижается (у тяжелых ядер). У урана ε ≈ 7,5 МэВ, а у средних ядер ε ≈ 8,5 МэВ. Средние ядра наиболее устойчивы, у них большая энергия связи. Отсюда открывается возможность получения энергии при делении тяжелого ядра на два более легких (средних). Такая ядерная реакция деления может осуществиться при бомбардировке ядра урана свободным нейтроном. Например, ²³⁵₉₂U делится на два новых ядра: рубидий₃₇^-94Rb и цезий ¹⁴⁰₅₅Cs (один из вариантов деления урана). Реакция деления тяжелого ядра замечательна тем, что помимо новых более легких ядер появляются два новых свободных нейтрона, которые называют вторичными. При этом на каждый акт деления приходится 200 МэВ выделяющейся энергии. Она выделяется в виде кинетической энергии всех продуктов деления и далее может быть использована, например, для нагревания воды или другого теплоносителя. Вторичные нейтроны в свою очередь могут вызвать деление других ядер урана. Образуется цепная реакция, в результате которой в размножающей среде может выделиться огромная энергия. Этот способ получения энергии широко используется в ядерных боеприпасах и управляемых ядерных энергетических установках на электростанциях и на транспортных объектах с атомной энергетикой.

Помимо указанного способа получения атомной (ядерной) энергии есть и другой – слияние двух легких ядер в более тяжелое ядро. Процесс объединения легких ядер может происходить лишь при сближении исходных ядер на расстояние, где уже действуют ядерные силы (сильное взаимодействие), то есть ~ 10^{– 15} м. Этого можно достигнуть при сверхвысоких температурах порядка 1 000 000 °C. Такие процессы называют термоядерными реакциями.

Термоядерные реакции в природе идут на звездах и, конечно, на Солнце. В условиях Земли они происходят при взрывах водородных бомб (термоядерное оружие), запалом для которых служит обычная атомная бомба, создающая условия для формирования сверхвысоких температур. Управляемый термоядерный синтез пока имеет только научно-исследовательскую направленность. Промышленных установок нет, однако работы в этом направлении ведутся во всех развитых странах, в том числе и в России.

2.11. Радиоактивность

Радиоактивностью называется самопроизвольное преобразование одних ядер в другие.

Спонтанный распад изотопов ядер в условиях природной среды называют естественной, а в условиях лабораторий в результате деятельности человека – искусственной радиоактивностью.

Естественную радиоактивность открыл французский физик Анри Беккерель в 1896 г. Это открытие вызвало революцию в естествознании вообще и в физике в частности. Классическая физика XIX в. с ее убежденностью в неделимости атома ушла в прошлое, уступив место новым теориям.

Открытие и исследование явления радиоактивности связано также с именами Марии и Пьера Кюри. Этим исследователям в 1903 г. была присуждена Нобелевская премия по физике.

Искусственная радиоактивность открыта и исследована супругами Ирен и Фредериком Жолио-Кюри, которые в 1935 г. также получили Нобелевскую премию.

Необходимо отметить, что принципиального различия между этими двумя типами радиоактивности нет.

Для каждого радиоактивного элемента установлены количественные оценки. Так, вероятность распада одного атома в одну секунду характеризуется постоянной распада данного элемента л, а время, за которое распадается половина радиоактивного образца, называется периодом полураспада Г₀₅.

Со временем число нераспавшихся ядер N убывает по экспоненциальному закону:

N = N₀e^-λt,

где N₀ – число нераспавшихся ядер в момент времени t = t₀ (то есть начальное число атомов), N – текущее значение числа нераспавшихся

ядер.

Этот закон называется элементарным законом радиоактивного распада. Из него можно получить формулу для периода полураспада:

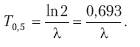
Число радиоактивных распадов в образце за одну секунду называют активностью радиоактивного препарата. Чаще всего активность обозначают буквой A тогда по определению:

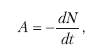
где знак «-» означает убывание N во времени.

Единица активности в системе СИ – Беккерель (Бк): 1 Бк=1распад/1с. Часто на практике используется внесистемная единица – Кюри (Ки), 1 Ки = 3,7 · 10¹⁰ Бк.

Можно показать, что активность уменьшается во времени также по экспоненциальному закону:

A = A₀ e^-λt.

Вопросы для самопроверки

1. Что такое материя? Какие виды материи различают в современном представлении?

2. Объясните понятие «элементарные частицы». Назовите важнейшие характеристики элементарных частиц. Как классифицируются элементарные частицы?

3. Сколько видов взаимодействия вам известно? Назовите их основные черты.

4. Что такое античастицы?

5. В чем заключается специфика изучения микромира по сравнению с изучением мега– и макромира?

6. Охарактеризуйте кратко историю развития представлений о строении атома.

7. Сформулируйте постулаты Н. Бора. Можно ли с помощью теории Н. Бора объяснить структуру атомов всех элементов таблицы Д. И. Менделеева?

8. Кто и когда создал теорию электромагнитного поля?

9. Что такое радиоактивность?

10. Назовите основные виды радиоактивного распада.

Глава 3 ПРОСТРАНСТВО, ВРЕМЯ, ПРИНЦИПЫ ОТНОСИТЕЛЬНОСТИ

3.1. Ньютоновская концепция абсолютного пространства и времени. Законы движения

Вопросы пространства и времени всегда интересовали человеческое общество. Одна из концепций этих понятий идет от древних атомистов – Демокрита, Эпикура и др. Они ввели в научный оборот понятие пустого пространства и рассматривали его как однородное и бесконечное.

В процессе создания общей картины мироздания Исаак Ньютон (1642–1726), конечно, также не мог обойти вопрос понятия пространства и времени.

В 1687 г. он опубликовал труд «Математические начала натуральной философии», который стал вершиной достижений естествознания XVII в.

По Ньютону, мир состоит из материи, пространства и времени. Эти три категории независимы друг от друга. Материя размещается в бесконечном пространстве. Движение материи происходит в пространстве и времени. Ньютон разделял пространство на абсолютное и относительное. Абсолютное пространство неподвижно, бесконечно. Относительное – это часть абсолютного. Так же он классифицировал и время. Подабсолютным, истинным (математическим) временем он понимал время, которое течет всегда и везде равномерно, а относительное время, по Ньютону, есть мера продолжительности, которая существует в реальной жизни: секунда, минута, час, сутки, месяц, год. У Ньютона абсолютное время существует и длится равномерно само по себе, безотносительно к каким-либо событиям. Абсолютное пространство и абсолютное время представляют собой вместилище всех материальных тел и пространств и не зависят ни от этих тел, ни от этих процессов, ни друг от друга.

Массу Ньютон определяет как количество материи и вводит понятие «пассивной силы» (силы инерции) и «активной силы», создающей движение тел.

Изучив и выявив закономерности движения, Ньютон таким образом сформулировал его законы:

1– й закон.Всякому телу продолжать свое состояние покоя или равномерного прямолинейного движения, поскольку оно не принуждается приложенными силами изменять это состояние.

2– й закон.Изменению движения быть пропорциональным приложенной движущей силе и происходить по направлению той прямой, по которой эта сила действует.

3– й закон.Действию всегда встречать равное противодействие, или воздействию двух тел друг на друга быть между собой равными и направленными в противоположные стороны.

В наше время знаменитые законы формулируются в более удобной форме:

► 1. Всякое материальное тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон называют также законом инерции.

► 2. Ускорение, приобретаемое телом, прямо пропорционально силе, действующей натело, и обратно пропорционально массе тела.

► 3. Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.

Второй закон Ньютона нам известен в виде

F = m × a, или a = F/m,

где ускорение а, получаемое телом поддействием силы F, обратно пропорционально массе тела m. Величина m называется инертной массой тела, она характеризует способность тела оказывать сопротивление действующей («активной») силе, то есть сохранять состояние покоя. Второй закон Ньютона справедлив только в инерциальных системах отсчета.

Первый закон можно получить из второго, так как в случае отсутствия воздействия на тело со стороны других сил ускорение также равно нулю. Однако первый закон рассматривается как самостоятельный закон, поскольку он утверждает существование инерциальных систем отсчета.

► Инерииальные системы отсчета – это такие системы, в которых справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы, взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.

Теоретически может существовать сколь угодно равноправных инерциальных систем отсчета, и во всех таких системах законы физики одинаковы. Это утверждает принцип относительности Галилея (1636 г.).

Научное доказательство существования всемирного тяготения и математическое выражение описывающего его закона стало возможным только на основе открытых И. Ньютоном законов механики. Закон всемирного тяготения был сформулирован Ньютоном в труде «Математические начала натуральной философии» (1687 г.).

Закон всемирного тяготения Ньютон формулирует в следующих тезисах: «тяготение существует для всех тел вообще и пропорционально массе каждого из них», «тяготение к отдельным равным частицам тел обратно пропорционально квадратам расстояний мест к частицам». Этот закон известен в виде:

где m₁, ш₂ – массы двух частиц, r – расстояние между ними, G – гравитационная постоянная (в системе СИ G = 6,672 · 10^-11 м²/кг²). Физический смысл гравитационной постоянной заключается в том, что она характеризует силу притяжения двух масс весом в 1 кг на расстоянии в 1 м.

Открыв закон всемирного тяготения, Ньютон смог дать ответ на вопрос, почему Луна обращается вокруг Земли и почему планеты движутся вокруг Солнца. В каждом отдельном случае он мог рассчитать силу тяготения. Но как передается взаимодействие между массами, притягивающимися друг к другу, какова природа этой силы, Ньютон объяснить не мог.

В трудах Ньютона тяготение – это сила, которая действует на больших расстояниях и как бы без какого-то материального посредника.

Это привело к понятию «дальнодействие». Природу «дальнодействия» Ньютон объяснить не мог. Он думал о каком-то материальном «агенте», с помощью которого осуществляется гравитационное взаимодействие, но в решении этой проблемы он потерпел неудачу. Основываясь на законе всемирного тяготения Ньютона, небесная механика допускает принципиальную возможность мгновенной передачи сигналов, что противоречит современной физике (общей теории относительности). Поэтому буквальное понимание закона тяготения Ньютона с современной точки зрения недопустимо.

Ньютоновская механистическая парадигма в естествознании господствовала более 200 лет, хотя и подвергалась критике по ряду позиций, в том числе и в понимании пространства и времени (Лейбниц, Гегель, Беркли и др.). В конце XIX и в начале XX в. возникли принципиально новые научные представления об окружающей природе. Появились новые парадигмы: сначала релятивистская, а затем квантовая (см. ранее). В физическую картину мира полноправно вошла концепция поля как материальной среды, связывающей частицы вещества, все физические объекты материального мира. В современной физике известны четыре вида взаимодействия материальных объектов: электромагнитное, гравитационное, сильное и слабое (см. выше). Они ответственны за все процессы взаимодействия.

3.2. Законы сохранения

Рассмотрим наиболее общие законы сохранения, которым подчиняется весь материальный мир и которые вводят в физику ряд фундаментальных понятий: энергия, количество движения (импульс), момент импульса, заряд.

Закон сохранения импульса

Как известно, количеством движения, или импульсом, называют произведение скорости на массу движущегося тела: p = mv Эта физическая величина позволяет найти изменение движения тела за какой-нибудь определенный промежуток времени. Для решения этой задачи следовало бы применять второй закон Ньютона бесчисленное число раз, во все промежуточные моменты времени. Закон сохранения количества движения (импульса) можно получить, используя второй и третий законы Ньютона. Если рассматривать две (или более) материальные точки (тела), взаимодействующие между собой и образующие систему, изолированную от действия внешних сил, то за время движения импульсы каждой точки (тела) могут изменяться, но общий импульс системы должен оставаться неизменным:

m₁v + m₁v₂ = const.

Взаимодействующие тела обмениваются импульсами при сохранении общего импульса.

В общем случае получаем:

где P_Σ – общий, суммарный импульс системы, m_iv_i – импульсы отдельных взаимодействующих частей системы. Сформулируем закон сохранения импульса:

► Если сумма внешних сил равна нулю, импульс системы тел остается постоянным при любых происходящих в ней процессах.

Пример действия закона сохранения импульса можно рассмотреть на процессе взаимодействия лодки с человеком, которая уткнулась носом в берег, а человек в лодке быстро идет из кормы в нос со скоростью v₁. В этом случае лодка отойдет от берега со скоростью v₂:

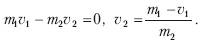
Аналогичный пример можно привести со снарядом, который разорвался в воздухе на несколько частей. Векторная сумма импульсов всех осколков равна импульсу снаряда до разрыва.