Лабораторная работа №3. Способы задания псевдографов и псевдоорграфов

Цель: Сформировать представление о спосбах задания графов, мультиграфов, псевдографов,орграфов, мультиорграфов и псевдоорграфов.

Результаты. После выполнения лабораторной работы должны сформироваться умения:

· строить интерактивные чертежи в программе GeoGebra;

· строить матрицы смежности, инцидентности графов, мультиграфов, псевдографов,орграфов, мультиорграфов и псевдоорграфов;

· знать различные способы задания графов, мультиграфов, псевдографов, орграфов, мультиорграфов и псевдоорграфов.

Теоретические сведения

1. Формальная постановка задачи:

Описание задач в терминах графов является очень абстрактным, так что если вам нужно реализовать решение, вы должны представить графы в виде каких-либо структур данных.

В общих словах, мы ищем способ реализации функции смежности, N(v), так, чтобы N[v] было каким-либо набором (или в отдельных случаях просто итератором) смежных с v вершин. Сосредоточимся на двух наиболее известных представлениях графов: списках смежности и матрицах смежности, потому что они наиболее полезны и обобщены.

Граф можно задать списком рёбер. Каждая строка этого списка соответствует одному ребру; в ней записаны имена вершин, инцидентных ему. Для неориентированного графа порядок вершин в строке произволен, для ориентированного графа сначала указывается начальная вершина, а затем - конечная.

Матрицей смежности графа является квадратная матрица C_n´n, столбцам и строкам которой соответствуют вершины. Для неориентированного графа элемент матрицы смежности c_ij равен количеству рёбер, инцидентных i-й и j-й вершинам; для ориентированного графа этот элемент равен количеству рёбер с началом в i-й вершине и концом в j-й вершине. Матрица смежности неориентированного графа симметрична (c_ij=c_ji) относительно главной диагонали. Для ориентированного графа она будет симметрична только в том случае, если для каждого ребра имеется ребро, соединяющее те же вершины, но идущее в противоположном направлении.

Списки смежности. Для каждой вершины создается список (или множество, или другой контейнер или итератор) смежных с ней вершин. Разберем простейший способ реализации такого списка, предположив, что имеется n вершин, пронумерованных 1,…, n. Вершины могут быть представлены любыми объектами и иметь собственные метки или имена. Однако использование целых чисел в диапазоне 1,…, n делает реализацию проще, так как номера вершин можно использовать как индексы. Каждый список смежности является списком таких номеров, а сами эти списки собраны в главный список размера n, индексированный номерами вершин. Обычно сортировка таких списков случайная, так что речь в действительности идет об использовании списков для реализации множества смежности. Термин список просто исторически устоялся.

Пусть v₁,v₂,...,v_n - вершины графа F; e₁,e₂,...,e_m - его рёбра. Отношение инцидентности можно определить матрицей инцидентности B_m´n , n столбцов которой соответствуют вершинам графа, а m строк - его рёбрам. Для неориентированного графа: b_ij=1, если ребро e_i инцидентно вершине v_j, в противном случае b_ij =0. В матрице инцидентности ориентированного графа, если вершина v_j - начало ребра e_i , то b_ij = -1, если v_j - конец e_i, то b_ij =1, если e_i - петля, а v_j - инцидентная ей вершина, то b_ij =a (где a - любое число, отличное от 1, 0, -1), в остальных случаях b_ij =0. В каждой строке матрицы инцидентности для неориентированного или ориентированного графа только два элемента отличны от нуля (или один, если ребро является петлёй), поэтому такой способ задания графа оказывается недостаточно экономным.

Для неориентированного псевдографа Γ количество r(v) рёбер, инцидентных вершине vÎΓ, называется локальной степенью или просто степенью этой вершины. Зная матрицу смежности или матрицу инцидентности графа, степень вершины v_j можно найти путём суммирования элементов j-го столбца матрицы инцидентности или матрицы смежности: r (v_j)= 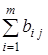r (v_j)= .

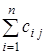При подсчёте степеней вершин по этим формулам каждая петля вносит в степень инцидентной ей вершины вклад 1. Однако при изображении петли на схеме к этой вершине примыкают два конца петли, т.е. петля вносит в эту степень вклад 2(петли расположены на главной диагонали матрицы смежности). Учёт вклада петель несколько усложняет формулы 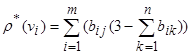.Когда i-е ребро обычное, 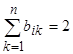, и r *(v_j)=r(v_j).

Если речь идёт о петле, то 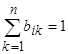,и слагаемое внешней суммы удваивается.

Соответствующая формула при заданной матрице смежности выглядит следующим образом: .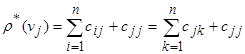

Первую из степеней ориентированного графа легко определить, суммируя элементы i-й строки матрицы смежности, а вторую - суммируя элементы i-го столбца:

r₁(v) = 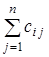; r₂(v)= .

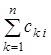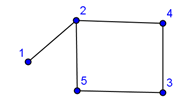2. Пример нахождения матрицы смежности, инцидентности, списка смежности, степеней вершин и диаграммы графа по списку ребер.