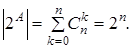Определение. (Интуитивный принцип абстракции)
Говорят, что всякий предикат P(x)задает некоторое множество A (быть может пустое), посредством условия, согласно которому в А входят те и только те элементы а, которые обращают P(а)в истинное высказывание.
Так как всякое множество однозначно определяется своими элементами, любой предикат определяет в точности одно множество А, обозначение:  .
.
Читается: множество таких элементов а, что P(а) – истинное высказывание. Возможны некоторые модификации записи  , смысл которых легко понять из контекста.
, смысл которых легко понять из контекста.
Пример 1. А =  - это множество точек окружности радиуса 1 с центром в начале координат.
- это множество точек окружности радиуса 1 с центром в начале координат.
Пример 2. А = 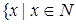 и x не имеет отличных от 1 делителей меньших или равных
и x не имеет отличных от 1 делителей меньших или равных 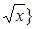 - это множество простых чисел.
- это множество простых чисел.
Пример 3. А = 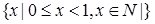 - пустое множество.
- пустое множество.
Замечание. В формулировках принципов объемности а абстракции используются два интуитивных понятия – множества и принадлежности элемента множеству. Неограниченное употребление этих понятий при построении характеристических предикатов приводит к парадоксам.
Сравнение множеств
Определение. Говорят, что множество Aсодержитсяво множестве B (А – подмножество B, А включено в B, В содержит/включает A), если всякий элемент множества A принадлежит и множеству В. В этом случае пишут: 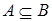 . Таким образом,
. Таким образом, 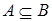 Û
Û 
Можно сказать иначе: если 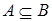 , то
, то  .
.
Одновременно верно и такое утверждение: если 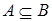 и
и 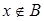 , то
, то 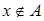 , ведь в противном случае
, ведь в противном случае 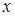 обязан принадлежать
обязан принадлежать 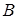 . Значит, можно записать: если
. Значит, можно записать: если 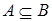 , то
, то 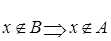 .
.
Определение. Говорят, что множество A естьсобственноеподмножество множества B (В строго включает А) и пишут A  В, если
В, если 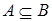 и В
и В  А.
А.
Таким образом, A  В Û
В Û 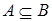 и
и 
Определение. Если 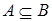 (A
(A  В), то множества А и В называются сравнимыми между собой.
В), то множества А и В называются сравнимыми между собой.
Ясно, что
·  A для всякого множества A;
A для всякого множества A;
· Если 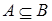 и
и  , то
, то  ; (
; (  и
и  , то
, то 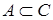 ).
).
Исходя из определения подмножества, опишем необходимые и достаточные условия того, что множество А не является подмножеством множества В (обозначение: А Ë В).
Именно, АËВ Û  Во множестве А должен существовать хотя бы один элемент, не принадлежащий множеству В.
Во множестве А должен существовать хотя бы один элемент, не принадлежащий множеству В.
Утверждение. 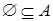 для всякого множества А.
для всякого множества А.
Доказательство. Пусть  . Тогда
. Тогда  . Но данное условие противоречиво, пустое множество не содержит элементов.
. Но данное условие противоречиво, пустое множество не содержит элементов.
Пример. Пусть В = {1, {2}, {1}, {2, 3}, {1, 3}} и А1 = {1, 2};
А2 = {1, {1}}; А3 = {2, 3}; А4 = {{2, 3}}; А5 = {1, {2, 3}, {1, 3}};
А6 = {1, Æ}; А7 = {{2}, {2, 3}, {1, 2, 3}}; А8 = Æ.
Тогда А1 Ë В (2 Ï В); А2 Í В; А3 Ë В (2 Ï В и 3 Ï В); А4 Í В; А5 Í В; А6 Ë В (Æ Ï В); А7 Ë В ({1, 2, 3} Ï В); А8 Í В.
Определение. Булеаном множества А (обозначается 2А) называется семейство всех подмножеств данного множества А.
Значит, 2А={B|B 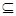 A}. В частности,
A}. В частности, 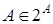 и
и 
Примеры булеанов.
Пусть  . Тогда
. Тогда 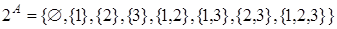 .
.
Пусть  . Тогда
. Тогда 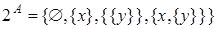 .
.
Пусть А = Æ. Тогда 2А = {Æ}.
Определение. Мощностью конечного множества А (обозначение:  ) называют число его элементов.
) называют число его элементов.
Пример. |Æ| = 0; |{Æ}| = |{x}| = 1; |{1, {1}, 2, {1, 2}}| = 4; |{{1, 2, 3, 4, 5}, Æ}| = 2.
Утверждение. Если  , то
, то 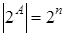 .
.
Доказательство. Число подмножеств множества А, содержащих k элементов, равно числу способов отобрать из n элементов множества А k элементов, образующих данное подмножество, т. е. равно 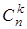 . Отсюда
. Отсюда