Задачи повышенной сложности

Задача 4.1

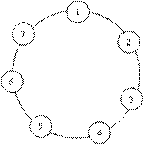В круге стоят N человек (рис.). Они пронумерованы от 1 до N. Поочередно из круга начинает выходить каждый третий человек. Это продолжается до тех пор, пока в круге не останется последний человек. Определить его номер.
Например, если в круге стояло 7 человек, то его поочерёдно покинут 3, 6, 2, 7, 5, 1. Оставшимся будет человек, стоявший на 4 месте.

Задача 4.2

Вывести на экран цифры числа 3¹⁰⁰⁰. Если попытаться получить число непосредственно умножением, компьютер выдаст сообщение об ошибке.

Задача 4.3

Написать программу для умножения двух чисел, количество цифр в каждом из которых может достигать 100. Например, для умножения вида:
9278969345897569872365*5705782370079678659.

Задача 4.4

Сообщество роботов живет по следующим законам: один раз в год они объединяются в полностью укомплектованные группы по 3 или 5 роботов (причем число групп из 3 роботов - максимально возможное). За год группа из 3 роботов собирает 5, а группа из 5 - 9 новых собратьев. Каждый робот живет 3 года после сборки. Известно начальное количество роботов (К>7), все они только что собраны. Определить сколько роботов будет через N лет.

Задача 4.5

На квадратном клетчатом листе бумаги 8x8 клеток заштрихована часть клеток (пример на рисунке). Определить вписанный в решётку прямоугольник максимальной площади, не содержащий заштрихованных клеток. В качестве ответа вывести площадь прямоугольника и координаты его двух противоположных вершин. (Предполагается, что прямоугольник с максимальной площадью один.)
Для приведенного примера координаты вершин (3,4) и (7,6), площадь 15 клеток.

Задача 4.6

На квадратном клетчатом листе бумаги n на m клеток нарисовано несколько фигур, каждая из которых состоит только из целых клеток. Различные фигуры не накладываются и не соприкасаются (пример на рисунке). Определить фигуру максимальной площади. (В качестве ответа вывести площадь фигуры и координаты одной из её точек. Предполагается, что фигура с максимальной площадью одна.)
Например, на листе 8 на 8 клеток:

Площадь фигуры равна 6. Координаты одной из её клеток (2,3).

Задача 4.7

Подсчитайте количество одно-, двух-, трёх- и четырехпалубных кораблей, расположенных на поле для игры "Морской бой". Корабли не могут быть изогнутыми и друг с другом не соприкасаются. Поле для игры задается в виде таблицы 10x10, каждый элемент которой равен либо 0, если клетка свободна, либо 1, если занята.

Задача 4.8

Лабиринт задан в виде матрицы размером n на m. Стенам лабиринта соответствуют единицы, проходам - нули. Определить, можно ли из точки с координатами (i₁, j₁) попасть в точку с координатами (i₂, j₂). Для усложнения задачи можно предложить указать самый короткий путь из заданной точки, причем из всех путей одинаковой длины выбирать путь с наименьшим числом поворотов.

Задача 4.9

На рисунке изображен треугольник из чисел. Вычислите наибольшую сумму чисел, расположенных на пути, начинающемся в верхней точке треугольника и заканчивающемся на его основании. Каждый шаг на пути может идти вниз по диагонали влево или вниз по диагонали вправо. Число строк в треугольнике больше1 и не больше100. Треугольник составлен из целых чисел от 0 до 99.

Задача 4.10

Имеется n населенных пунктов, пронумерованных от 1 до n. Некоторые пары пунктов соединены дорогами (в том числе дорогами с односторонним движением). Определить, можно ли попасть по этим дорогам из одного заданного пункта в другой. (Для усложнения задачи можно предложить указать все возможные пути без петель и тупиков из одного пункта в другой).

Задача 4.11

Заданы две фразы. Определить наибольшую последовательность отличных от пробелов символов, входящую в обе фразы в одном и том же порядке. Например, в предложениях:
ПРИШЛА ВЕСНА и РАСТАЯЛ СНЕГ такая последовательность - Р,А,С,Н.

Задача 4.12

В морском порту города Владивостока хранятся N контейнеров (N - чётное число). Для погрузки контейнеров на судно, чтобы обеспечить равномерную загрузку, их необходимо разделить на две половины так, чтобы их массы были максимально близки. Решить эту задачу, предполагая, что информация о массах контейнеров (в тоннах) хранится в массиве M(N). В качестве ответа указать номера контейнеров одной половины и получаемые массы для каждой из половин.
Например:
Если M(6)=(10, 15, 18, 20, 16, 14), то одну половину составят 1, 4, 5 контейнеры (другую 2, 3, 6). Масса первой группы m1=10+20+16=46 т., масса второй группы m2=15+18+14=47 т.

Задача 4.13

На шахматной доске необходимо расставить 8 ферзей так, чтобы они не угрожали друг другу.

Задача 4.14

На шахматной доске размером 4x4 клетки расставить 4 ладьи так, чтобы они не угрожали друг другу. Определить все такие расстановки (всего их будет 24).

Решения задач

Задача 4.2

Для записи больших чисел удобно использовать массивы, записывая цифры числа как элементы массива. Оценим количество цифр, необходимых для записи 3¹⁰⁰⁰:
3² = 9; 3¹⁰⁰⁰ = (3²)⁵⁰⁰ = 9⁵⁰⁰ 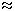10⁵⁰⁰.
Таким образом, в записи этого числа будет менее 500 цифр.
Запишем вначале в массив только число 3 и далее будем умножать его поэлементно на 3 нужное число раз, учитывая перенос из разряда в разряд, возникающий при умножении.
Программа, решающая эту задачу, может быть записана, например, так:

const stp=1000;var i,j,k,prn,x:integer; a:array [1..500] of integer;begin a[500]:=3; prn:=0; for i:=2 to stp do for j:=500 downto 1 do begin x:=a[j]*3; a[j]:=(x+prn) mod 10; prn:=(x+prn) div 10; end; k:=1; while (a[k]=0) do k:=k+1; for i:=k to 500 do write(a[i]:1); writeln

end.

Здесь stp - степень, в которую возводится число 3, a[500] - массив, в котором хранятся цифры полученного числа, prn - перенос из разряда в разряд. Объём вычислений в данной программе можно значительно сократить, если каждый раз умножать на 3 не весь массив a, а только его занятую часть.

Задача 4.3

Принцип решения этой задачи такой же, как и у предыдущей. Результат умножения двух стозначных чисел будет не превышать по размеру 200 знаков (т.е. для хранения результата понадобится массив из 200 элементов). Для ввода исходных чисел удобно использовать строковый тип данных.

Задача 4.4

Рассмотрим следующий вариант решения. Создадим массив R(3), где R₁, R₂, R₃ - количество роботов соответствующего возраста. Тогда общее количество роботов S= R₁+ R₂+ R₃. Обозначим x - количество троек, y - количество пятерок, которое можно сформировать из общего числа роботов (идея разбиения на тройки и пятерки рассмотрена в задаче 1.5). Каждый год роботы стареют, общее количество роботов увеличивается на 5x+9y и уменьшается на R₃ (число роботов, проживших 3 года). Программа решения может быть записана так:

var k,i,n,p:integer; s,x,y:longint; r:array [1..3] of longint;begin write('Начальное количество роботов k='); readln(k); write('Число лет n='); readln(n); r[1]:=k; r[2]:=0; r[3]:=0; s:=k; for i:=1 to n do begin x:=s div 3; p:=s mod 3; if p=0 then y:=0 else if p=1 then begin x:=x-3; y:=2 end else begin x:=x-1; y:=1 end; r[3]:=r[2]; r[2]:=r[1]; r[1]:=5*x+9*y; s:=r[1]+r[2]+r[3]; end; writeln('s=',s)end.

В этой программе использовался тип longint, предназначенный для хранения больших целых чисел (до 2147483647). Это связано с тем, что общее число роботов увеличивается очень быстро. Так, например, если начальное число роботов - 10, то через 10 лет их будет 143702.

Задача 4.5

Представим лист бумаги в виде числовой матрицы А(8x8). Обозначим заштрихованные клетки единицами, а чистые - нулями.
Данную программу удобно реализовать, используя подпрограммы. Напишем подпрограмму, которая проверяет, есть ли в прямоугольнике с координатами левой верхней вершины (i1,j1) и координатами правой нижней вершины (i2,j2) заштрихованные клетки (т.е. элементы, равные 1).

function prov(a:matr;i1,j1,i2,j2:integer):boolean;var i,j:integer;begin prov:=true; for i:=i1 to i2 do for j:=j1 to j2 do if a[i,j]=1 then prov:=false;end;

Эта функция будет возвращать значение "истина" (true), если заштрихованных клеток в рассматриваемом прямоугольнике нет, и "ложно" (false) - в противном случае.
В основной программе организуем два попарно вложенных цикла: в первом цикле будут изменяться координаты верхнего левого угла рассматриваемого прямоугольника, во втором - координаты нижнего правого угла. Если в прямоугольнике нет заштрихованных точек, то вычислим его площадь, и если она является максимальной, запомним её и координаты противоположных вершин этого прямоугольника. Часть основной программы, реализующая данный алгоритм, будет иметь следующий вид:

maxs:=0; for i1:=1 to n do for j1:=1 to n do for i2:=i1 to n do for j2:=j1 to n do begin s:=(i2-i1+1)*(j2-j1+1); if prov(a,i1,j1,i2,j2)and(maxs<s) then begin maxs:=s; maxi1:=i1; maxj1:=j1; maxi2:=i2; maxj2:=j2; end; end;writeln(' s=',maxs);writeln('(',maxi1,',',maxj1,')', '(',maxi2,',',maxj2,')');

Здесь maxs - площадь полученного прямоугольника, (maxi1, maxj1) - координаты его левой верхней вершины, (maxi2, maxj2) - координаты его правой нижней вершины.

Задача 4.6

Подобные задачи достаточно просто реализуются с использованием рекурсии. Решение построим следующим образом: представим лист в виде числовой матрицы А(nxm). Обозначим заштрихованные клетки единицами, а чистые - нулями. Напишем рекурсивную процедуру, которая определяет площадь заштрихованной фигуры и заменяет клетки уже просмотренной фигуры двойками (чтобы не просматривать эту фигуру ещё раз). В основной программе организуем цикл перебора всех элементов матрицы. Если очередной элемент равен 1 (ещё не просмотренная фигура), то будем вызывать процедуру определения площади этой фигуры).
Процедура рекурсивного определения площади фигуры будет иметь вид:

procedure zaliv(i,j:byte; var s:integer);begin a[i,j]:=2; s:=s+1; if (i+1<=n)and(a[i+1,j]=1) then zaliv(i+1,j,s); if (j+1<=m)and(a[i,j+1]=1) then zaliv(i,j+1,s); if (j-1>0)and(a[i,j-1]=1) then zaliv(i,j-1,s); if (i-1>0)and(a[i-1,j]=1) then zaliv(i-1,j,s);end;

Здесь n и m - число столбцов и строк в рассматриваемой матрице, i, j - координаты найденной клетки фигуры, s - переменная, в которой накапливается площадь фигуры. Процедура учитывает найденную клетку в площади, потом проверяет, заштрихована ли клетка, которая расположена ниже просматриваемой (если это не последняя строка), и если да, то рекурсивно вызывается с этой клетки, потом тот же процесс повторяется для клеток расположенных справа, слева и сверху от рассматриваемой. Рабочая часть основной программы будет иметь вид:

max:=0; im:=0; jm:=0;for i:=1 to n dofor j:=1 to m do if a[i,j]=1 then begin s:=0; zaliv(i,j,s); if s>max then begin max:=s; im:=i; jm:=j; end; end;writeln('Smax=',max,' im=',im,' jm=',jm);

Здесь max - переменная, в которой хранится максимальная площадь фигуры, im, jm - координаты первой найденной точки этой фигуры.

Задача 4.8

Наиболее простым способом решения задач по поиску пути является рекурсивный поиск. Его алгоритм во многом аналогичен рассмотренному в задаче 4.6.
Пусть A(nxm) - матрица, задающая лабиринт (1 - стена, 0 - проход). Напишем процедуру рекурсивного перемещения по лабиринту. Путь прохода будем отмечать цифрами, начиная с 2 (2, 3, 4 и т.д.). Пусть на k-том шаге мы попали на клетку с координатами (i, j). Если это та клетка, путь до которой необходимо было отыскать (с координатами (i₂, j₂)), то задача решена. Необходимо распечатать матрицу с отмеченным путем и прекратить выполнение программы. Если нет, то необходимо проверить, можно ли перейти на соседнюю клетку (справа, слева, сверху или снизу), и если возможно, то вызвать процедуру перемещения уже с этой клетки. Если перехода на соседнюю клетку нет, то необходимо очистить исходную клетку, чтобы её можно было использовать в других вариантах при поиске пути. Обозначим move(i,j,k) - процедуру рекурсивного перемещения (i, j - номер клетки, k - номер шага), writematr - процедуру, распечатывающую матрицу A, тогда программа, реализующая предложенный алгоритм, может быть записана следующим образом:

const n=4; m=5;type matr=array [1..n,1..m] of integer;{Матрица, задающая варианты прохода. 1-стена; 0-проход.}const labir:matr=((1,0,0,0,1), (0,0,1,0,1), (1,0,0,0,0), (0,0,1,0,0));var a:matr; i1,j1,i2,j2,f:byte; k:integer;procedure writematr;var i,j:byte;beginfor i:=1 to n do begin for j:=1 to m do write(a[i,j]:3,' '); writeln; endend;procedure move(i,j:byte; k:integer);begin a[i,j]:=k; k:=k+1; if (i=i2)and(j=j2) then begin writematr; f:=1; halt end else begin if (i+1<=n)and(a[i+1,j]=0) then move(i+1,j,k); if (j+1<=m)and(a[i,j+1]=0) then move(i,j+1,k); if (j-1>0)and(a[i,j-1]=0) then move(i,j-1,k); if (i-1>0)and(a[i-1,j]=0) then move(i-1,j,k); end; a[i,j]:=0; k:=k-1;end;begin a:=labir; writeln('Координаты i1, j1'); readln(i1,j1); writeln('Координаты i2, j2'); readln(i2,j2); f:=0; k:=2; if(a[i1,j1]=1)or(a[i2,j2]=1) then writeln ('Неверные координаты') else move(i1,j1,k); if f=0 then writeln('Прохода нет');end.

Здесь - labir - матрица-константа 4x5, задающая пример лабиринта, f - переменная, через которую отслеживается, есть ли проход из начальной точки в конечную или нет, процедура halt - стандартная процедура, которая прекращает выполнение программы.
Если взять в качестве начальной точки точку с координатами (4, 1), в качестве конечной - точку с координатами (1, 4), то рассмотренная программа выдаст следующий вариант прохода:

1 0 0 8 1
0 0 1 7 1
1 4 5 6 0
2 3 1 0 0

Задача 4.11

Для решения этой задачи рассмотрим стандартную задачу перебора всех возможных сочетаний элементов некоторого массива. Пусть X(n) - массив с элементами 1, 2, … n (массив номеров). Напишем программу, которая на основе этого массива генерирует все подмножества номеров, состоящие из m элементов.
Например, при n=5, m=3. X(5)=(1,2,3,4,5)
Подмножества из 3-х номеров: (1,2,3), (1,2,4), (1,2,5), (1,3,4), (1,3,5), (1,4,5), (2,3,4), (2,3,5), (2,4,5), (3,4,5). Порядок перебора, рассмотренный в примере, называется лексикографическим. Такой порядок подобен расположению слов в словаре: сначала сравниваются первые буквы, потом вторые и т.д. Всего сочетаний из n элементов по m будет 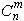(см. задачу 2.3), то есть .
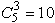Для упрощения структуры программы напишем процедуру, которая печатает первые m элементов массива X(n) (предположим, что массив описан глобально):

procedure printm(m:integer);var i:integer;begin for i:=1 to m do write(x[i],' '); writeln;end;

Далее рассмотрим функцию, которая на основе очередного сочетания получает следующее по порядку сочетание:

function posl(m:integer):boolean;var j,f:integer;label 10,20;begin f:=0; posl:=true; for j:=m downto 1 do if x[j]=n+j-m then f:=j else begin inc(x[j]); goto 10 end;10: if f<>0 then if f=1 then begin posl:=false; goto 20 end else for j:=f to m do x[j]:=x[f-1]+j-f+1;20:end;

Эта функция возвращает значение "истина" (true), если переданное сочетание не последнее (для рассмотренного примера: (1,3,4) или (2,4,5)), и значение "ложь" (false), если переданное в функцию сочетание последнее (для рассмотренного примера - (3,4,5)). Функция использует только первые m элементов массива X(n). В первом цикле проверяется, можно ли увеличить какой-либо из элементов массива (начиная с последнего). Если можно увеличить последний (m-й) элемент, то он увеличивается, служебной переменной f присваивается значение 0, и происходит выход из функции (например, из последовательности (1,2,4) получается последовательность (1,2,5)). Если последний элемент уже нельзя увеличить (например, последовательность (1,4,5)), то находится элемент, который еще можно увеличить (в данном случае 1), этот элемент увеличивается, а во втором цикле вслед за ним выстраиваются остальные (таким образом, из (1,4,5) получим (2,3,4)). В этом случае в f сохраняется номер элемента, следующего за увеличенным.
Программа, печатающая все сочетания из n элементов по m (при n=5, m=3), будет иметь вид:

const n=5;var x:array[1..n] of integer; m,j:integer;…{Описание процедур printm и posl}…beginm:=3;for j:=1 to m do x[j]:=j;repeat printm(m);until not posl(m);end.

Удобство написанной функции в том, что, для получения всех возможных сочетаний из n номеров достаточно добавить в основную часть программы цикл по m:

begin for m:=n downto 1 do begin for j:=1 to m do x[j]:=j; repeat printm(m); until not posl(m); end;end.

Для решения основной задачи необходимо удалить из обеих строк пробелы, далее перебирать в порядке убывания длины сочетания из букв одной строки и проверять, входят ли они в другую (если да, то решение найдено). Программа, решающая задачу, будет иметь вид:

const k=255;var x: array [1..k] of integer; m,n,j: integer; s1,s2,s: string;label 1;…{Описание процедуры posl}…procedure prints(m:integer);var i:integer;begin write(m,': '); for i:=1 to m do write(s1[x[i]]); writeln; readln;end;function spc(s:string):string;var str:string; i:integer;begin str:=''; for i:=1 to length(s) do if s[i]<>' ' then str:=str+s[i]; spc:=str;end;function equal(m:integer):boolean;var i,j:integer;begin j:=1; for i:=1 to length(s2) do if (s1[x[j]]=s2[i])and(j<=m) then j:=j+1; if j>m then equal:=true else equal:=false;end;begin writeln('Введите первую строку'); readln(s1); writeln('Введите вторую строку'); readln(s2); s1:=spc(s1); s2:=spc(s2); if (length(s2)<length(s1)) then begin s:=s1; s1:=s2; s2:=s end; n:=length(s1); for m:=n downto 1 do begin for j:=1 to m do x[j]:=j; repeat if equal(m) then begin prints(m); goto 1; end; until not posl(m); end;1:end.

В этой программе процедура prints печатает найденную последовательность символов и её длину, функция equal проверяет, входит ли очередная последовательность, составленная из символов одной строки в другую, функция spc удаляет из переданной в неё строки пробелы.
Работу полученной программы можно значительно ускорить, если добавить в неё часть, в которой перед началом перебора из обеих строк удалялись бы те символы, которые встречаются только в одной из них. (Например, заданные в условии строки после такого преобразования приняли бы вид: РЛАЕСНА и РАСАЛСНЕ).

Задача 4.13

Эта задача решена во многих книгах по программированию (например, в [4,5]). Так как ферзей 8, то очевидно, что на каждой вертикали и горизонтали будет стоять по одному ферзю, поэтому можно считать, что ферзь с номером k стоит на k-той вертикали и необходимо найти его координату по горизонтали.

Задача 4.14

Как и в предыдущей задаче, будем считать, что на каждой вертикали стоит по ладье, и для каждой из них необходимо найти координату по горизонтали (причем не совпадающую с соответствующими координатами остальных ладей). Таким образом, исходная задача сводится к нахождению всех возможных перестановок из 4 элементов. Известно, что число перестановок из n элементов равно n!=1*2*3*…*n. Например, из 3 элементов можно получить 3!= 1*2*3=6 перестановок:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
Так как алгоритмы перестановок часто используются в олимпиадных задачах, рассмотрим их подробнее. Наиболее коротким и простым для запоминания является рекурсивный алгоритм получения перестановок. Пусть X[n] - массив, элементы которого числа от 1 до n. Для упрощения программы будем использовать процедуру printm, печатающую массив X, и процедуру swap(a,b), меняющую местами значения переменных a и b. Тогда программа рекурсивного получения перестановок (при n=4) будет иметь вид:

const n=4;var x:array [1..n] of integer; i:integer; procedure printm;var i:integer;begin for i:=1 to n do write(x[i],' '); writeln;end;procedure swap(var a,b:integer);var v:integer;begin v:=a; a:=b; b:=vend;procedure perest(k:integer);var i:integer;begin if k=n-1 then printm else for i:=k+1 to n do begin swap(x[k+1],x[i]); perest(k+1); swap(x[k+1],x[i]); end;end;begin for i:=1 to n do x[i]:=i; perest(0);end.

Эта программа работает по следующему принципу: первоначально процедура perest будет рекурсивно вызываться до тех пор, пока не будет распечатан исходный массив X (без перестановки элементов):
1 2 3 4
Потом произойдет отход на шаг назад, перестановка двух последних элементов, и при очередном вызове печать получившегося массива:
1 2 4 3
после чего массив вернется в первоначальное состояние.
Потом произойдет еще один отход назад и перестановка последнего и третьего с конца элементов, после чего процедура будет снова рекурсивно вызываться, пока не будет распечатан массив X:
1 4 3 2
Далее опять будут переставлены два последних элемента:
1 4 2 3
и т.д. Особенность данного алгоритма в том, что после окончания он оставляет исходный массив X без изменений. Из программ, которые не используют рекурсию, рассмотрим следующую:

const n=4;label 10,20,30;var x,c:array[1..n] of integer; i,j:integer;…{описание процедур swap и printm}…begin for i:=1 to n do x[i]:=i; printm; for i:=2 to n do c[i]:=1; 20: for i:=2 to n do begin if c[i]<>i then goto 10; for j:=2 to i do c[j]:=1; end; goto 30; 10: for j:=1 to trunc(i/2) do swap(x[j],x[i+1-j]); printm; c[i]:=c[i]+1; goto 20; 30:end.

Массив X(n) в этой программе - массив номеров, массив C(n) - служебный массив, который используется для отслеживания числа сделанных перестановок.