Свойства частиц и взаимодействий 6 страница
Таким образом Bц >1 кэВ при l  0, т.е. нейтроны с энергией
0, т.е. нейтроны с энергией 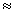 1 кэВ могут эффективно взаимодействовать с ядрами только при l = 0, при этом волновая функция относительного движения сферически симметрична, а угловое распределение изотропно в с.ц.и.
1 кэВ могут эффективно взаимодействовать с ядрами только при l = 0, при этом волновая функция относительного движения сферически симметрична, а угловое распределение изотропно в с.ц.и.
44. Определить энергию возбуждения составного ядра, образующегося при захвате  -частицы с энергией T = 7 МэВ неподвижным ядром 10В.
-частицы с энергией T = 7 МэВ неподвижным ядром 10В.
При взаимодействии  -частицы ядром 10В образуется составное ядро 14N. Напишем закон сохранения энергии в с.ц.и.
-частицы ядром 10В образуется составное ядро 14N. Напишем закон сохранения энергии в с.ц.и.
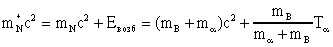 .
.
Откуда для Eвозб получим
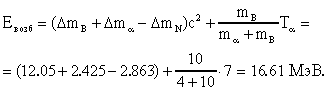
45. В сечении реакции 27Аl (  ,р) 30Si наблюдаются максимумы при энергиях
,р) 30Si наблюдаются максимумы при энергиях  -частиц T 3.95; 4.84 и 6.57 МэВ. Определить энергии возбуждения составного ядра, соответствующие максимумам в сечении.
-частиц T 3.95; 4.84 и 6.57 МэВ. Определить энергии возбуждения составного ядра, соответствующие максимумам в сечении.
В данной реакции образуется составное ядро 31P. По аналогии с задачей 44:
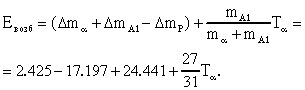
Подставляя значения энергий T, получим
Евозб = 13.11; 13.88 и 15.39 МэВ.
46. С каким орбитальным моментом могут рассеиваться протоны с Тр = 2 МэВ на ядре 112Sn?
Воспользуемся формулой (3.10):
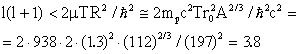 .
.
Таким образом протоны с энергией 2 МэВ взаимодействуют с ядром 112Sn при l = 0 и l = 1.
47. Оценить сечение образования составного ядра при взаимодействии нейтронов с кинетической энергией Tn = 1 эВ с ядрами золота 197Au.
При этой энергии с ядром эффективно будут взаимодействовать нейтроны только с l = 0. Воспользуемся формулой (3.20) для оценки сечения образования составного ядра:
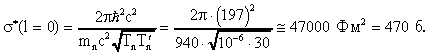
48. Оценить сечение образования составного ядра при взаимодействии нейтронов с кинетической энергией Tn = 30 МэВ с ядрами золота 197Au.
Для оценки сечения в этой области энергий можно воспользоваться формулой (3.18)
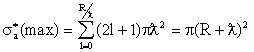
Оценим длину волны нейтрона
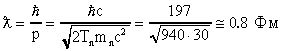 ,
,
так как R>> 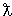 , можно записать
, можно записать
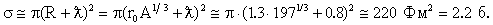
49. Сравнить полные сечения реакции для  -частиц с энергией 20 Мэв на ядрах 56Fe и 197Au.
-частиц с энергией 20 Мэв на ядрах 56Fe и 197Au.
В реакциях с заряженными частицами при относительно небольших энергиях основным фактором, определяющим величину сечения, является высота кулоновского барьера. Оценим высоту кулоновского барьера по формуле (3.11a)
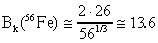 МэВ,
МэВ, 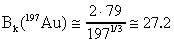 МэВ.
МэВ.
Энергия  -частиц больше высоты кулоновского барьера на ядре 56Fe и меньше высоты кулоновского барьера на ядре 197Au. Следовательно полное сечение реакций на ядре 197Au будет сильно подавлено и меньше, чем сечение реакции на ядре 56Fe.
-частиц больше высоты кулоновского барьера на ядре 56Fe и меньше высоты кулоновского барьера на ядре 197Au. Следовательно полное сечение реакций на ядре 197Au будет сильно подавлено и меньше, чем сечение реакции на ядре 56Fe.
50. Оценить сечение реакции 63Cu(p,n)63Zn, если известны сечения реакций, идущих с образованием того же составного ядра с той же энергией возбуждения:
60Ni(  ,p)63Zn - 0.7 б; 63Cu(p,pn)62Cu - 0.87 б; 60Ni(
,p)63Zn - 0.7 б; 63Cu(p,pn)62Cu - 0.87 б; 60Ni(  ,pn)62Cu - 0.97 б.
,pn)62Cu - 0.97 б.
Все приведенные реакции идут через одно и то же составное ядро 64Zn:
- 63Cu + p
 64Zn
64Zn  n + 63Zn;
n + 63Zn; - 60Ni +

 64Zn
64Zn  p + 63Zn;
p + 63Zn; - 63Cu + p
 64Zn
64Zn  p + n + 62Cu;
p + n + 62Cu; - 60Ni +

 64Zn
64Zn  p + n + 62Cu.
p + n + 62Cu.
Для таких реакций справедливо соотношение (3.13)
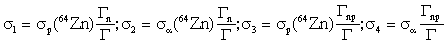 ,
,
где Гn, Гpn - ширины распада составного ядра с вылетом нейтрона и нейтрона + протона, Г - полная ширина распада. Отсюда получаем, что
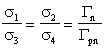 ,
,
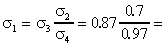 0.63 б.
0.63 б.
51. Оценить нейтронную ширину Гn изолированного уровня 0+ ядра 108Rh (энергия уровня E0 =1.21 эВ, полная ширина Г = 0.21 эВ), если при резонансном поглощении нейтронов с образованием этого уровня составного ядра сечение поглощения для энергии нейтронов Tn = 1 эВ ab 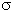 = 2700 б. Спин ядра-мишени I(107Rh) = 1/2.
= 2700 б. Спин ядра-мишени I(107Rh) = 1/2.
Сечение резонансной реакции (n,  ) (3.21)
) (3.21)
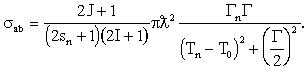
Длина волны нейтрона
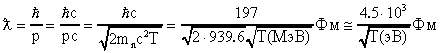 .
.
Полная ширина уровня
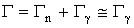 .
.
В итоге получим
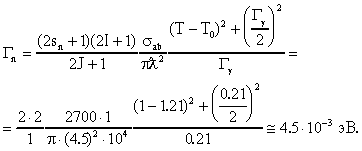
52. Получить, исходя из модели оболочек, отношение сечений реакций подхвата 16O(p,d) 15O, с образованием конечного ядра 15O в основном состоянии (JP =1/2-) и в состоянии (JP =3/2-).
Особенностью реакций подхвата (p,d) является то, что в них возбуждаются состояния, соответствующие возбуждению "дырок" относительно основного состояния ядра-мишени. В реакции 16O(p,d) это состояния (1p1/2)-1 и (1p3/2)-1, глубокие дырочные состояния (1s1/2)-1 не возбуждаются, если энергия налетающей частицы не очень велика (взаимодействие поверхностное). Основному состоянию ядра 15O (JP =1/2-) соответствует нейтронная конфигурация
(1s1/2)2(1p3/2)4(1p1/2)1,
а состоянию с JP =3/2- - конфигурация
(1s1/2)2(1p3/2)3(1p1/2)2.
То есть в первом случае подхватывается нейтрон из состояния 1p1/2, а во втором из 1p3/2. Вероятности подхвата в первую очередь определяются числом нейтронов на соответствующих подоболочках. Таким образом сечение реакции с образованием ядра 15O в основном состоянии должно быть приблизительно вдвое меньше, чем сечение реакции с возбуждением состояния ядра 3/2-.
53. Для реакции срыва 35Cl(d,p)36Cl найти возможные значения орбитального момента ln захваченного ядром нейтрона. Указать, исходя из простейшей оболочечной модели, какое из значений ln реализуется, если ядро 36Cl образуется в основном состоянии.
Спины и четности ядер 35Cl и 36Cl 3/2+ и 2+ соответственно. Из закона сохранения количества движения следует, что
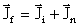 ,
,
где Ji и Jf - спины ядер 35Cl, и 36Cl, соответственно, а Jn - полный момент нейтрона
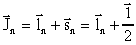
|Ji -Jf| < Jn < Ji + Jf
1/2 < Jn < 7/2
или 0 < ln < 4.
Из закона сохранения четности
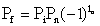 ,
, 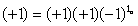 ,
,
где Pi, Pf, Pn - четности начального и конечного ядер и нейтрона, получаем, что ln - четное число, ln = 0, 2, 4. Ядро 35Cl в оболочечной модели в основном состоянии имеет нейтронную конфигурацию
(1s1/2)2(1p3/2)4(1p1/2)2(1d5/2)6(2s1/2)2(1d3/2)2.
Конечное ядро 36Cl имеет еще один нейтрон в состоянии 1d3/2 с орбитальным моментом 2. Это значение переданного момента нейтрона и реализуется в реакции 35Cl(d,p)36Cl с возбуждением основного состояния конечного ядра.
54. Оценить спин и четность состояния ядра 24Mg с энергией 1.37 МэВ, если при возбуждении этого состоянии в реакции неупругого рассеяния  -частиц с энергией T = 40 Мэв, первый максимум в угловом распределении
-частиц с энергией T = 40 Мэв, первый максимум в угловом распределении  -частиц наблюдается под углом 100.
-частиц наблюдается под углом 100.
Воспользовавшись фомулой (3.23) получим,
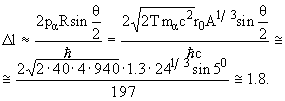
Орбитальный момент может принимать только целочисленные значения, таким образом ближайшее значение  l = 2. Спин и четность основного состояния ядра 24Mg
l = 2. Спин и четность основного состояния ядра 24Mg 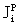 = 0+. Используя закон сохранения момента количества движения, получим
= 0+. Используя закон сохранения момента количества движения, получим
|Ji - 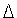 l| < Jj < Ji +
l| < Jj < Ji +  l ,
l ,
отсюда Jf = 2. Четность этого состояния, согласно закону сохранения четности должна быть положительной, таким образом квантовые характеристики состояния с энергией 1.37 МэВ 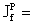 2+.
2+.
55. Найти угол , под которым должен быть максимум углового распределения протонов в реакции (d,p) на ядре 58Ni, вызванной дейтронами с энергией T=15 МэВ, с образованием ядра 59Ni в основном состоянии.
Спин и четность ядра 58Ni 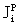 = 0+. В данном случае пере-даваемый угловой момент l равен угловому моменту нейтрона, помещаемого в состояние 2p3/2, l = 1. Используя формулу (3.22), получим
= 0+. В данном случае пере-даваемый угловой момент l равен угловому моменту нейтрона, помещаемого в состояние 2p3/2, l = 1. Используя формулу (3.22), получим
Свойства частиц и взаимодействий
1. 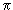 0-мезон, кинетическая энергия которого равна энергии покоя, распадается на два
0-мезон, кинетическая энергия которого равна энергии покоя, распадается на два  - кванта, энергии которых равны. Каков угол между направлениями движения
- кванта, энергии которых равны. Каков угол между направлениями движения  -квантов?
-квантов?
Энергии  -квантов в л.с. равны, если равны углы вылета
-квантов в л.с. равны, если равны углы вылета  -квантов относительно направления первоначального движения пиона. По условию задачи T = mc2, где T - кинетическая энергия, m - масса пиона. Тогда для полной энергии Ei и импульса
-квантов относительно направления первоначального движения пиона. По условию задачи T = mc2, где T - кинетическая энергия, m - масса пиона. Тогда для полной энергии Ei и импульса 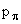 пиона можно записать
пиона можно записать
Ei = Т + mc2 = 2T,
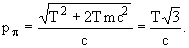
Из закона сохранения энергии 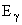 = T. Закон сохранения импульса приводит к следующему соотношению
= T. Закон сохранения импульса приводит к следующему соотношению
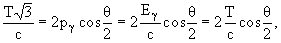
где 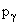 - импульс одного
- импульс одного  -кванта. Откуда
-кванта. Откуда
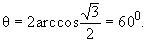
2. Определить величину суммарной кинетической энергии p - мезонов 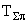 , образующихся при распаде покоящегося K+ -мезона: K+
, образующихся при распаде покоящегося K+ -мезона: K+ 
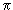 + +
+ + 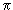 + +
+ + 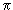 -. Массы покоя частиц в энергетических единицах:
-. Массы покоя частиц в энергетических единицах:
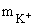 = 493.646 МэВ,
= 493.646 МэВ, 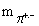 = 139.658 МэВ.
= 139.658 МэВ.
Полная энергия K+-мезона 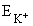 равна его энергии покоя
равна его энергии покоя 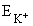 =
= 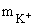 . Полная энергия трех пионов
. Полная энергия трех пионов 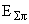 равна сумме их кинетических энергий и энергий покоя
равна сумме их кинетических энергий и энергий покоя 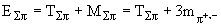 . Из закона сохранения энергии
. Из закона сохранения энергии 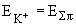 ,
,
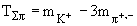 = (493.646 МэВ – 3x139.658 МэВ) = 74.672 МэВ.
= (493.646 МэВ – 3x139.658 МэВ) = 74.672 МэВ.
3. Определить частицы X, образующиеся в реакциях сильного взаимодействия:
1) 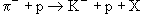 ; 2)
; 2) 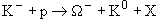 ; 3)
; 3) 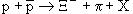 .
.
Исходя из законов сохранения электрического заряда Q, барионного заряда B, странности S и проекции изоспина I3 в этих реакциях определим характеристики частиц X:
| 1) | 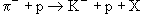 | ||
| Q: | -1 + 1  -1 + 1 + QX -1 + 1 + QX | QX = 0 | |
| B: | 0 + 1  0 + 1 + BX 0 + 1 + BX | BX = 0 | |
| S: | 0 + 0  -1 + 0 + SX -1 + 0 + SX | SX = 1 | |
| I3: | - 1 + 1/2  -1/2 + 1/2 + (I3)X -1/2 + 1/2 + (I3)X | (I3)X = -1/2 |
Этот набор квантовых чисел соответствует K0-мезону.
| 2) | 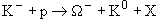 | ||
| Q: | -1 + 1  -1 + 0 + QX -1 + 0 + QX | QX = 1 | |
| B: | 0 + 1  1 + 0 + BX 1 + 0 + BX | BX = 0 | |
| S: | -1 + 0  -3 + 1 + SX -3 + 1 + SX | SX = 1 | |
| I3: | -1/2 + 1/2  0 - 1/2 + (I3)X 0 - 1/2 + (I3)X | (I3)X = 1/2 |
Этот набор квантовых чисел соответствует K+-мезону.
| 3) | 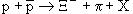 | ||
| Q: | 1 - 1  -1 + 1 + QX -1 + 1 + QX | QX = 0 | |
| B: | 1 - 1  1 + 0 + BX 1 + 0 + BX | BX = - 1 | |
| S: | 0 + 0  -2 + 0 + SX -2 + 0 + SX | SX = 2 | |
| I3: | 1/2 - 1/2  -1/2 + 1 + (I3)X -1/2 + 1 + (I3)X | (I3)X = - 1/2 |
Этот набор квантовых чисел соответствует 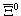 -гиперону.
-гиперону.
4. Могут ли следующие реакции: 1) 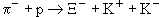 ; 2)
; 2) 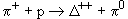 ; 3)
; 3) 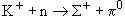 происходить в результате сильного взаимодействия.
происходить в результате сильного взаимодействия.
Определим изменения электрического заряда Q, барионного заряда B, странности S и проекции изоспина I3 в этих реакциях:
| 1) | 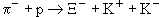 | ||
| Q: | -1 + 1  -1 + 1 -1 -1 + 1 -1 |  Q = - 1 Q = - 1 | |
| B: | 0 + 1  1 + 0 + 0 1 + 0 + 0 |  B = 0 B = 0 | |
| S: | 0 + 0  -2 + 1 - 1 -2 + 1 - 1 |  S = - 2 S = - 2 | |
| I3: | - 1 + 1/2  -1/2 + 1/2 -1/2 -1/2 + 1/2 -1/2 |  I3 = 0 I3 = 0 |
Реакция невозможна, так как не сохраняются электрический заряд и странность.
| 2) | 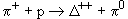 | ||
| Q: | 1 + 1  2 + 0 2 + 0 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 1 + 0 |  B = 0 B = 0 | |
| S: | 0 + 0  0 + 0 0 + 0 |  S = 0 S = 0 | |
| I3: | 1 + 1/2  3/2 + 0 3/2 + 0 |  I3 = 0 I3 = 0 |
Реакция возможна, так как все законы сохранения выполнены.
| 3) | 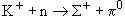 | ||
| Q: | 1 + 0  1 + 0 1 + 0 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 1 + 0 |  B = 0 B = 0 | |
| S: | 1 + 0  -1 + 0 -1 + 0 |  S = - 2 S = - 2 | |
| I3: | 1/2 -1/2  1 + 0 1 + 0 |  I3 = 1 I3 = 1 |
Реакция невозможна, так как не сохраняются странность и проекция изоспина.
5. Какие из приведенных ниже реакций под действием антинейтрино возможны, какие запрещены и почему: 1) 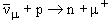 ; 2)
; 2) 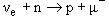 ; 3)
; 3) 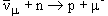 .
.
Реакции происходят в результате слабого взаимодействия. Определим изменения электрического заряда Q, барионного заряда B, лептонного электронного Le и мюонного 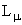 чисел в этих реакциях:
чисел в этих реакциях:
| 1) |  | ||
| Q: | 0 + 1  0 + 1 0 + 1 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 1 + 0 |  B = 0 B = 0 | |
| Le: | 0 + 0  0 + 0 0 + 0 |  Le = 0 Le = 0 | |
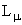 : : | -1 + 0  0 -1 0 -1 |  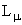 = 0 = 0 |
Реакция возможна, так как все законы сохранения выполнены.
| 2) | 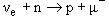 | ||
| Q: | 0 + 0  1 -1 1 -1 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 1 + 0 |  B = 0 B = 0 | |
| Le: | -1 + 0  0 + 0 0 + 0 |  Le = 1 Le = 1 | |
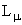 : : | 0 + 0  0 + 1 0 + 1 |  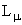 = 1 = 1 |
Реакция невозможна, так как не сохраняются электронное и мюонное лептонные числа.
| 3) | 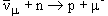 | ||
| Q: | 0 + 0  1 -1 1 -1 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 1 + 0 |  B = 0 B = 0 | |
| Le: | 0 + 0  0 + 0 0 + 0 |  Le = 0 Le = 0 | |
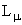 : : | - 1 + 0  0 + 1 0 + 1 |  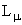 = 2 = 2 |
Реакция невозможна, так как не сохраняется мюонное лептонное число.
