Свойства частиц и взаимодействий 5 страница

Построим импульсную диаграмму:

1. Отложим отрезок (AB) = p_a, где p_a - величина импульса налетающей частицы в л.с..

1. На отрезке (AB) отложим точку O, которая делит (AB) на отрезки пропорциональные массам продуктов реакции:

.

1. Из точки O деления импульса p_a проводим окружность с радиусом равным величине импульсов продуктов реакции в с.ц.и. .
2. Из точки A проводим прямую до пересечения с окружностью. Отрезок (AC) равен импульсу вылетающей частицы b в л.с., а угол - углу вылета этой частицы в л.с., угол - углу вылета частицы b в с.ц.и..
3. Из точки С опустим перпендикуляр (CD) на прямую (AB), тогда можно записать:

,

, . Комбинируя эти три уравнения, получим

где (см. (2.28))

Окончательно получим

где

.

23. Протон с кинетической энергией Т_a= 5 МэВ налетает на ядро ¹Н и упруго рассеивается на нем. Определить энергию T_B и угол рассеяния _B ядра отдачи ¹Н, если угол рассеяния протона _b = 30⁰.

Для упругого рассеяния

T_a = T_b + T_B,

где T_a, T_b, и T_B - кинетические энергии налетающего протона, рассеянного протона и ядра водорода после рассеяния в л.с..
Из (2.30) имеем

,

.

В итоге получим

МэВ,

.

24.Для получения нейтронов широко используется реакция t(d,n) . Определить энергию нейтронов T_n, вылетающих под углом 90⁰ в нейтронном генераторе, использующем дейтроны, ускоренные до энергии Т_d = 0.2 МэВ.

Определим энергию реакции:

Q = 13.136 + 14.950 - 2.424 - 8.071 = 17.591 МэВ.

Используем соотношение (2.30) получим

.

25.Для получения нейтронов используется реакция ⁷Li(p,n)⁷Be. Энергия протонов T_p = 5 МэВ. Для эксперимента необходимы нейтроны с энергией T_n = 1.75 МэВ. Под каким углом _n относительно направления протонного пучка будут вылетать нейтроны с такой энергией? Какой будет разброс энергий нейтронов T, если их выделять с помощью коллиматора размером 1 см, расположенного на расстоянии 10 см от мишени.

Расчитаем энергию реакции
Q = 14.907 + 7.289 - 8.071 - 15.768 = -1.643 МэВ
Используя (2.31), получим

Диапазон углов, вырезаемых коллиматором
Используя (2.30), получим

26. Определить орбитальный момент трития l_t, образующегося в реакции ²⁷Al( ,t)²⁸Si, если орбитальный момент налетающей -частицы = 0.

	+ 27Al	= t	+ 28Si
JP: 0+	5/2+	1/2+	0+

Момент количества движения во входном канале

Из закона сохранения момента количества движения следует:

Откуда 3, 2.

Четности во входном и выходном каналах

;

,

Из закона сохранения четности:

Орбитальный момент трития l_t должен быть четным числом, т.е. l_t = 2.

27.При каких относительных орбитальных моментах количества движения протона возможна ядерная реакция p + ⁷Li ⁸Be^* + ?

p	+7Li	8Be*		+
JP: 1/2+	3/2-		0+	0+

Четность в конечном состоянии

Волновая функция двух тождественных бозонов ( -частиц) при пространственном отражении не меняется, т.е. волновая функция должна быть симметрична относительно перестановки бозонов. Отсюда следует, что - четное число. Полный момент системы в конечном состоянии J_f = и, соответственно может принимать только четные значения. Следовательно, промежуточное ядро ⁸Be для того, чтобы развалится на две -частицы должно быть в состояниях с положительной четностью и четными значениями спина. Четность в начальном состоянии также должна быть положительной

Таким образом, чтобы выполнялся закон сохранения четности орбитальный момент налетающего протона должен быть нечетным числом (l_p= 1,3, ...).

28. С какими орбитальными моментами l_p могут вылетать протоны в реакции ¹²C( ,p )¹¹B, если: 1) конечное ядро образуется в основном состоянии, а поглотился Е2- фотон; 2) конечное ядро образуется в состоянии 1/2⁺, а поглотился М1- фотон; 3) конечное ядро образуется в основном состоянии, а поглотился Е1- фотон?

В основном состоянии J^P(¹²C) = 0⁺.

1) J^P(¹¹B) = 3/2^-.

Воспользуемся законом сохранения четности и момента количества движения. В начальном соcтоянии:

В конечном состоянии :

.

В соответствии с законом сохранения момента, орбитальный момент протона l_p может принимать значения 0,1,2,3,4. Из закона сохранения четности

следует, что четные значения l_p должны быть отброшены, т.е. протоны могут вылетать с орбитальными моментами l_p =1,3.

2) J^P(¹¹B) = 1/2⁺.

В соответствии с законом сохранения момента l_p может принимать значения 0, 1, 2. Из закона сохранения четности орбитальный момент протонов должен быть четным l_p =0, 2.

3) J^P(¹¹B) = 3/2^-.

Из допустимых законом сохранения момента значений 0, 1, 2 закон сохранения четности оставляет только четные значения l_p =0, 2.

30. В результате поглощения ядром ⁴Не -кванта вылетает нейтрон с орбитальным моментом l_n = 2. Определить мультипольность -кванта, если конечное ядро образуется в основном состоянии.

Реакция ⁸Be(p, )⁷Li.

В конечном состоянии

В начальном состоянии

Следовательно фотоны должны иметь положительную четность и мультипольности 1, 2, 3, т.е. это М1, Е2 и М3-фотоны.

31. Ядро ⁸Ве поглощает -квант, в результате чего вылетает протон с орбитальным моментом l = 1. Определить мультипольность поглощенного -кванта, если конечное ядро образуется в основном состоянии?

В начальном состоянии

В конечном состоянии

Из закона сохранения момента следует, что возможные значения орбитального момента дейтрона l_d= 0 ,1 ,2 . Однако закон сохранения четности допускает только нечетные значения, т.е. l_d = 1.

33. Ядро ⁴⁰Cа поглощает Е1 -квант. Какие одночастичные переходы возможны?

Согласно одночастичной модели спин и четность основного состояния ядра - 0⁺. В ядре полностью заполненны оболочки , , . Оболочка вакантна. При поглощении Е1 фотона, по законам сохранения момента и четности квантовые характеристики ядра в возбужденном состоянии должны быть 1^-. Наиболее низколежащим состояниям, которые будут возбуждаться, будут соответствовать одночастичные переходы нуклонов из третьей оболочки в четвертую вакантную оболочку. При этом будут образовываться состояния типа частица - дырка 1p1h. Спин таких состояний

,

где и - полные моменты частицы и дырки соответственно. Этому условию соответствуют следующие переходы: 1d3/2 2p3/2, 1d3/2 1f5/2, 1d3/2 2p1/2, 2s1/2 2p3/2, 2s1/2 2p1/2, 1d5/2 1f7/2, 1d5/2 2p3/2, 1d5/2 1f5/2. При этом закон сохранения четности также выполняется, так как переходы происходят в состояния с противоположной четностью. При поглощении Е1-фотонов достаточно большой энергии возможно возбуждение и других частично-дырочных состояний. Например при переходе нуклонов из первой оболочки в четвертую, это переходы 1s1/2 2p3/2 и 1s1/2 2p1/2.

34. Ядро ¹²C поглощает Е1 -квант. Какие одночастичные переходы возможны ?

Основное состояние ядра ¹²C имеет спин и четность 0⁺, у него полностью заполнены первая оболочка и подоболочка 1p_3/2 второй оболочки, При поглощении Е1 фотонов возможны переходы нуклонов из второй оболочки на третью и из первой оболочки на вакантные состояния второй таких, чтобы суммарный момент частицы и дырки в образовавшемся состоянии типа частица - дырка был равен 1, при этом закон сохранения четности будет выполнен, так как четность состояний при переходе от первой ко второй и от второй к третьей оболочке меняется и четность таких состояний будет отрицательной. Это переходы 1s_1/2 2p_3/2, 1p_3/2 1d_5/2, 1p_3/2 2s_1/2, 1p_3/2 1d_3/2.

36. Вычислить сечение рассеяния -частицы с энергией 3 МэВ в кулоновском поле ядра ²³⁸U в интервале углов от 150⁰ до 170⁰.

Воспользуемсяформулой Резерфорда для дифференциального сечения упругого рассеяния нерелятивистской заряженной частицы на угол в кулоновском поле ядра (3.6):

,

где T - кинетическая энергия налетающей частицы, z и Z - заряды налетающей частицы и ядра мишени соответственно. Сечение рассеяния -частицы в интервале углов ₁ - ₂:

фм² = 7.86 б.

37. Золотая пластинка толщиной d = 0.1 мм облучается пучком -частиц с интенсивностью N₀ = 10³ частиц/c. Кинетическая энергия -частиц T = 5 МэВ. Сколько -частиц на единицу телесного угла падает в секунду на детектор, расположенный под углом = 170⁰? Плотность золота 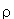= 19.3 г/см³.

Воспользуемся формулами (3.2) и (3.3):

(3.2)

. (3.3)

Рассеяние чисто резерфордовское, тогда дифференциальное сечения упругого рассеяния (3.6):

. (3.6)

Комбинируя (3.2), (3.3) и (3.6) получим для числа -частиц, попадающих в детектор за 1 секунду:

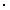0.77 частиц/(рад с).

38. Коллимированный пучок -частиц с энергией T = 10 МэВ падает перпендикулярно на медную фольгу толщиной = 1 мг/см². Частицы, рассеянные под углом = 30, регистрируются детектором площадью S = 1см², расположенным на расстоянии l = 20 см от мишени. Какая доля от полного числа рассеянных -частиц будет зарегистрирована детектором?

Аналогично задаче 37

,

где ; =S/4l².

Тогда доля частиц, рассеянных под углом =30 ⁰:

39. При исследовании реакции ²⁷Al(p,d)²⁶Al под действием протонов с энергией T_p = 62 МэВ в спектре дейтронов, измеренном под углом _d = 90 с помощью детектора с телесным углом d = 2·10^-4 ср, наблюдались пики с энергиями T_d = 45,3; 44,32; 40.91 МэВ. При суммарном заряде протонов q = 2.19 мКл, упавших на мишень толщиной = 5 мг/см², количество отсчетов в этих пиках N составило 5180, 1100 и 4570 соответственно. Определить энергии уровней ядра ²⁶Al, возбуждение которых наблюдалось в этой реакции. Рассчитать дифференциальные сечения 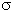d /d этих процессов.

Энергия возбуждения ядра определяется соотношением

Е_b⁽ⁱ⁾=Q₀-Q_i,

где Q₀, Q_i - энергии реакций с образованием ядра в основном и возбужденном состояниях соответственно.
Энергия реакции ²⁷Al (p, d)²⁶Al с образованием ²⁶Al в основном состоянии получим, используя данные по избыткам масс атомов

Q₀ = -17.197 + 7.289 -13.136 + 12.210 = -10.834 МэВ.

Энергию реакции, можно рассчитать с помощью соотношения (2.31):

.

Подставляя в него соответствующие величины получим для трех пиков соответственно

Q₁ = -10.83 МэВ, Q₂ = -11.87 МэВ и Q₃ = - 15.56 МэВ.

Таким образом первый пик соответствует образованию ядра ²⁶Al в основном состоянии (Q₁ = Q₀ ) , второй возбуждению состояния с энергией 1.05 МэВ, а третий 4.72 МэВ
Количество частиц мишени на единицу площади:

Полное число упавших на мишень частиц

частиц

40. Интегральное сечение реакции ³²S( ,p)³¹P с образованием конечного ядра ³¹P в основном состоянии при энергии падающих -квантов, равной 18 МэВ, составляет 4 мб. Оценить величину интегрального сечения обратной реакции ³¹P(p, )³²S, отвечающей той же энергии возбуждения ядра ³²S, что и в реакции ³²S( ,p)³¹P. Учесть, что это возбуждение снимается за счет -перехода в основное состояние.

Воспользуемся принципом детального равновесия для реакции (3.8):

где , .

Энергии фотона E и вылетающего протона T_p связаны соотношением

,

где энергия реакции

Q = 26.016 + 24.441 7.289 = 8.864 МэВ,

T_p = 18-8.864 = 9.136 МэВ.

Частицы обладающие нулевой массой имеют не более двух ориентаций спина: параллельную и антипараллельную ее импульсу, безотносительно к величине спина. Поэтому соотно-шение детального баланса в этом случае имеет вид:

мб.

41. Рассчитать интенсивность пучка нейтронов J, которым облучали пластинку ⁵⁵Mn толщиной d=0.1 см в течении t_акт = 15 мин, если спустя t_охл = 150 мин после окончания облучения ее активность I составила 2100 Бк. Период полураспада ⁵⁶Mn 2.58 ч, сечение активации 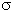= 0.48 б, плотность вещества пластины 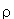= 7.42 г/см³.

Для активности пластины можно записать

,

где n - число ядер на единицу площади мишени

.

Отсюда

1.6210⁷ нейтр./с

42. Дифференциальное сечение реакции 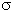d /d под углом 90⁰ составляет 10 мб/ср. Рассчитать величину интегрального сечения, если угловая зависимость дифференциального сечения имеет вид 1+2sin.

Найдем константу a из условия a(1 + 2sin90⁰) = 10. a = 10/3 мб/ср. В результате получим

108 мб.

43. Рассеяние медленных (T_n 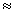1 кэВ) нейтронов на ядре изотропно. Как можно объяснить этот факт?

Оценим высоту центробежного барьера тяжелого ядра ²³⁸U для нейтронов