Свойства частиц и взаимодействий 1 страница

Введение

1. Чему равна скорость частицы v, кинетическая энергия T которой равна ее энергии покоя mc²?

Полная энергия релятивистской частицы

.

В случае T = mc², получаем

,

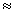откуда v = c 0.87 c.

2. На каком расстоянии интенсивность пучка мюонов с кинетической энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины первоначального значения?

Уменьшение интенсивности пучка мюонов происходит в результате распада мюонов

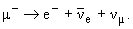
Число мюонов N(t), не распавшихся к моменту времени t, определяется соотношением

N(t) = N(0) exp(-t/ ),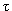

2.1

где 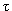- среднее время жизни мюона, N(0) - число мюонов в начальный момент времени. Среднее время жизни покоящихся мюонов равно 2.2 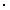10^{- 6} с. В данном случае

N(t) = N(0)/2 = N(0) exp(-t/ ),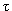

2.2

то есть exp(- t/ 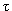) = 1/2, или же t = 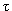ln2. Релятивистское замедление течения времени определяется соотношением

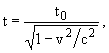2.3

где t₀ - время в системе, связанной с движущимся телом. В нашем случае получаем

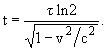2.4

Связь между кинетической энергией T и импульсом p частицы

2.5

Релятивистский импульс частицы

2.6

где m - масса покоя частицы, v - ее скорость. Из (2.5) и (2.6) получим

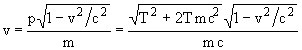2.7

Энергия покоя mc² мюона 106 МэВ. Пробег мюона

l = v t

2.8

Подставляя в (2.8) (2.4) и (2.7), получим

3. Ядро ¹⁰B из возбужденного состояния с энергией 0.72 МэВ распадается путем испускания -квантов с периодом полураспада T_1/2 = 6.7 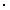10^-10 с. Оценить неопределенность в энергии E испущенного -кванта.

Из соотношения неопределенностей Гейзенберга получим

где 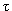-среднее врямя жизни возбужденного состояния.

4. Рассчитать длины волн 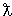протона и электрона с кинетической энергией T = 10 МэВ.

Протон нерелятивистский (T_p << m_pc²). В этом случае

,

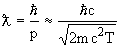учитывая, что 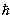c = 197 МэВ 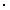Фм , имеем

Электрон релятивистский (T_e >> m_ec²). В этом случае

5. Протон, электрон и фотон имеют одинаковую длину волны 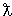= 10^{- 9} см. Какое время t им необходимо для пролета расстояния L = 10 м?

Для протона и электрона:

/

т.е.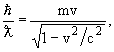

откуда получаем, что

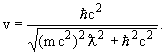
Время пролета

.

Протон:

Электрон:

Фотон:

6. Длина волны фотона 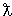= 3 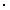10^-11см. Вычислить импульс p фотона.

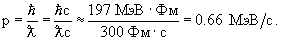
Свойства атомных ядер

1. Альфа-частицы с кинетической энергией T = 6.5 МэВ испытывают резерфордовское рассеяние на ядре золота ¹⁹⁷Au. Определить: 1) параметр столкновения bдля альфа-частиц, наблюдаемых под углом = 90⁰; 2) минимальное расстояние r_min сближения альфа-частиц с ядром; 3) кинетическую (T^') и 4) потенциальную (E^') энергии альфа-частиц в этой точке.

1) Угол , на который рассеивается нерелятивистская заряженная частица в кулоновском поле неподвижного ядра, определяется соотношением

где Z₁ - заряд частицы, а Z₂ - заряд ядра. Тогда

2) Запишем в полярных координатах закон сохранения энергии

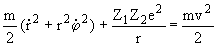
и закон сохранения момента импульса

.

При r = r_min производная = 0. Получаем систему уравнений:

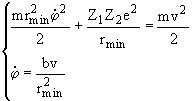
Подставив второе уравнение в первое и учитывая выражение для b, получаем

3) Потенциальная энергия частицы в точке наибольшего сближения с ядром

и, соответственно,

4) кинетическая энергия

T' = T - E' = 6.5 МэВ - 5.4 МэВ = 1.1 МэВ.

2. Протон с кинетической энергией T = 2 МэВ налетает на неподвижное ядро ¹⁹⁷Au. Определить дифференциальное сечение рассеяния на угол = 60° . Как изменится величина дифференциального сечения рассеяния, если в качестве рассеивающего ядра выбрать ²⁷Al?

Дифференциальное сечение упругого кулоновского рассеяния на угол определяется формулой Резерфорда

,

где Z₁ - заряд налетающей частицы, Z₂ - заряд ядра. Тогда

Из формулы Резерфорда следует, что отношение дифференциальных сечений рассеяния при замене ядра ¹⁹⁷Au на ²⁷Al будет определяться отношением квадратов зарядов этих ядер:

то есть при одинаковых условиях сечение рассеяния на золоте будет в 37 раз больше, чем на алюминии.

3. Вычислить сечение рассеяния a -частицы с кинетической энергией T = 5 МэВ кулоновским полем ядра ²⁰⁸Pb под углами больше 90⁰.

Искомое сечение получим интегрированием формулы Резерфорда

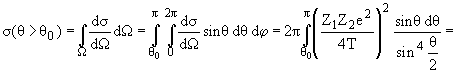
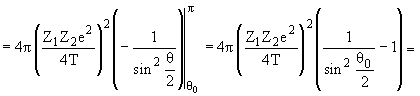
4. Золотая пластинка толщиной l = 1 мкм облучается пучком - частиц с плотностью потока
j = 10⁵ частиц/см² 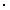с. Кинетическая энергия - частиц T = 5 МэВ. Сколько - частиц на единицу телесного угла падает в секунду на детектор, расположенный под углом = 170° к оси пучка? Площадь пятна пучка на мишени S = 1 см².

Число частиц, рассеянных в единицу времени в единичный телесный угол равно , где n - число ядер на единицу площади поверхности мишени, а - дифференциальное сечение упругого рассеяния.
Число ядер на единицу площади поверхности мишени

где 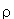- плотность вещества мишени, l - ее толщина, A - массовое число вещества мишени и N_A - число Авогадро.
Поток частиц через детектор

5. Рассчитать дифференциальное сечение 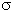d /d упругого рассеяния протонов на ядрах золота ¹⁹⁷Au под углом 15° , если известно, что за сеанс облучения мишени толщиной d = 7 мг/см² протонами с суммарным зарядом Q = 1 нКл на детектор площадью S = 0.5 см², расположенный на расстоянии l = 30 см от мишени, попало N = 1.97 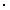10⁵ упруго рассеянных протонов. Сравнить экспериментально измеренное сечение с резерфордовским.

Дифференциальным сечением реакции a + A B + b называется величина

,

где n - количество частиц мишени на единицу площади, N - количество попавших на мишень частиц a, 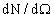- количество частиц, продуктов данной реакции b, вылетевших в элемент телесного угла d в направлении, характеризуемом полярным и азимутальным углами. Дифференциальное сечение обычно измеряется в барнах на стерадиан.

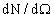= N/ , = S/l², N = Q/e_p, n = d 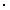N_A/A , где e_p - заряд протона, N_A - число Авогадро и A - массовое число ядра ¹⁹⁷Au. Дифференциальное сечение будет

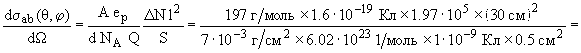
= 2.65 10³ б/ср.

Дифференциальное сечение упругого кулоновского рассеяния по формуле Резерфорда для протонов с кинетической энергией T = 3 МэВ:

Полученная величина близка к экспериментально измеренному сечению.

6. При упругом рассеянии электронов с энергией T = 750 МэВ на ядрах ⁴⁰Ca в сечении наблюдается дифракционный минимум под углом _min = 18° . Оценить радиус ядра ⁴⁰Ca.

Положение первого минимума в сечении упругого рассеяния _min можно оценить с помощью формулы для дифракции плоской волны на диске радиуса R

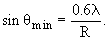
Учитывая, что электроны ультра релятивистские, получаем

7. Эмпирическая зависимость радиуса ядра R от числа нуклонов A (A > 10) R 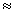r₀A^1/3.
Параметр r₀ 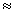1.23 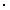10^-13 см = 1.23 Фм приблизительно одинаков для всех ядер.
Оценить радиусы атомных ядер ²⁷Al, ⁹⁰Zr, ²³⁸U.

Для ²⁷Al R = 1.23 Фм ^x 27^1/3 = 3.7 Фм.

Для ⁹⁰Zr R = 1.23 Фм ^x 90^1/3 = 5.5 Фм.

Для ²³⁸U R = 1.23 Фм ^x 238^1/3 = 7.6 Фм.

8. Оценить плотность ядерной материи.

Масса одного нуклона в ядре m_N 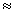1 а.е.м. = 1.66 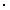10^-24 г. Плотность ядерной материи есть масса ядра, деленная на его объем

Плотность ядерной материи не зависит от A.

9. Массы нейтрона и протона в энергетических единицах равны соответственно m_n = 939.6 МэВ и m_p = 938.3 МэВ. Определить массу ядра ²H в энергетических единицах, если энергия связи дейтрона E_св(2,1) =2.2 МэВ.

Масса ядра M(A,Z) = Zm_p + (A–Z)m_n – E_св(A,Z), где Z и A - соответственно заряд и масса ядра. Тогда для дейтрона

M(2,1) = 1 ^x 938.3 МэВ + 1 ^x 939.6 МэВ – 2.2 МэВ = 1875.7 МэВ.

10. Масса нейтрального атома ¹⁶O m_ат(A,Z) = 15.9949 а.е.м. Определить удельную энергию связи 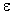ядра ¹⁶O.

Удельная энергия связи ядра

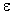(A,Z) = E_св(A,Z)/A,

где E_св(A,Z) - энергия связи ядра, A - массовое число. Полная энергия связи ядра

E_св(A,Z) = [Zm_p + (A-Z)m_n - m_я(A,Z)]c² = [Zm_p + (A-Z)m_n - m_ат(A,Z) - Zm_e]c²

Используя энергетические единицы для масс 1а.е.м.= 931.49 МэВ, получаем для ядра ¹⁶O

= 7.5 МэВ/нуклон.

11. Массы нейтральных атомов в а.е.м.: ¹⁶O - 15.9949, ¹⁵O - 15.0030, ¹⁵N - 15.0001. Чему равны энергии отделения нейтрона и протона в ядре ¹⁶O?

Энергия отделения нейтрона

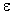_n(A,Z) = m_n +m(A-1,Z) - m(A,Z),

протона

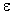_p(A,Z) = m_p +m(A-1,Z-1) - m(A,Z).

В обеих формулах массы должны быть в энергетических единицах.

Для ядра ¹⁶O

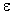_n = 939.6 МэВ + (15.0030 а.е.м. - 15.9949 а.е.м.)^х931.5 МэВ = 15.6 МэВ,
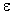_p = 938.3 МэВ + (15.0001 а.е.м. - 15.9949 а.е.м.)^х931.5 МэВ = 15.6 МэВ.

12. С помощью формулы Вайцзеккера рассчитать энергии отделения нейтронов в четно-четных изотопах ³⁸Ca, ⁴⁰Ca, ⁴⁸Ca.

Энергия отделения нейтрона в ядре (A,Z)

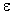_n(A,Z) = [m_n + m(A-1,Z) - m(A,Z)]c².

Масса ядра

m(A,Z)c² = [Zm_p + (A-Z)m_n]c² - E_св(A,Z).

Энергия отделения нейтрона

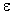_n(A,Z) = [m_n + Zm_p + (A-1-Z)m_n]c² - E_св(A-1,Z) - [Zm_p + (A-Z)m_n]c² + = E_св(A,Z) - E_св(A-1,Z).

Энергия связи атомных ядер описывается с помощью формулы Вайцзеккера

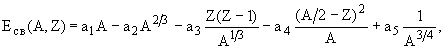
где a₁ = 15.78 МэВ, a₂ = 17.8 МэВ, a₃ = 0.71 МэВ, a₄ = 94.8 МэВ, a₅ = 0 для ядер с нечетным A, a₅ = +34 МэВ для четно- четных ядер и a₅ = - 34 МэВ для нечетно- нечетных ядер.

Тогда для ядер (A,Z) энергия связи будет:

³⁸Ca

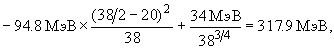
⁴⁰Ca

⁴⁸Ca


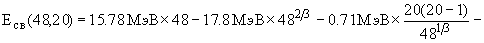
Для ядер (A -1,Z) энергия связи будет:

³⁷Ca


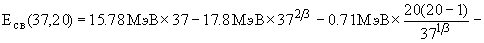
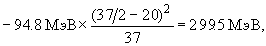
³⁹Ca


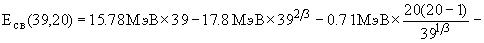
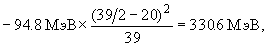
⁴⁷Ca

.

Энергия отделения нейтрона:

³⁸Ca 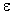_n(38,20) = 317.9 МэВ - 299.5 МэВ = 18.4 МэВ,

⁴⁰Ca 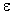_n(40,20) = 346.3 МэВ - 330.6 МэВ = 15.7 МэВ,

⁴⁸Ca 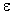_n(48,20) = 418.4 МэВ - 410.3 МэВ = 8.1 МэВ.

13. Считая, что разность энергий связи зеркальных ядер определяется только различием энергий кулоновского отталкивания в этих ядрах, вычислить радиусы зеркальных ядер ²³Na, ²³Mg. E_св(²³Na) = 186.56 МэВ, E_св(²³Mg) = 181.72 МэВ.

Кулоновская энергия равномерно заряженного шара радиуса R определяется соотношением

Обозначим заряд ядра ²³Na как Z, а ядра ²³Mg как Z + 1. Тогда разность энергий связи ядер ²³Na и ²³Mg будет

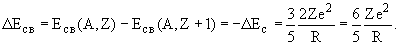
Для радиуса ядра получаем

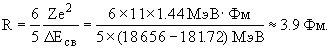
На основе эмпирической зависимости R = 1.23 A^1/3 Фм получаем R(²³Mg) = R(²³Na) 1.23 ^x 23^1/3 =3.5 Фм.

14. Ядро ²⁷Si в результате ⁺-распада 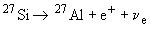переходит в "зеркальное" ядро ²⁷Al. Максимальная энергия позитронов 3.48 МэВ. Оценить радиус этих ядер.

Разность энергий связи двух зеркальных ядер

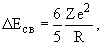
где R - радиус ядра, e - заряд электрона и Z - атомный номер, в данном случае ядра ²⁷Al, откуда

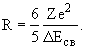
Максимальная энергия спектра позитронов при ⁺-распаде
= E_св – 1.80 МэВ.
Тогда для радиуса ядра можно записать следующее соотношение

Модели ядер

1. А. Нейтрон и протон находятся в состояниях с |l,s,j>_n = |1,¹/₂,³/₂>, |l,s,j>_p = |1,¹/₂,³/₂>. Какие значения может иметь полный момент системы j?
Б. Два нейтрона находятся в состояниях |l,s,j>₁ = |1,¹/₂,³/₂> и |l,s,j>₂ = |1,¹/₂,³/₂>. Какие значения может иметь полный момент системы j?

В случае А нейтрон и протон не являются тождественными частицами, поэтому полный момент системы | j₁ – j₂ | < j < j₁ + j₂, то есть j = 0, 1, 2, 3.
В случае Б значения j = 1, 3 запрещены принципом Паули, т.к. в этом случае тождественные частицы будут иметь одинаковый набор квантовых чисел l, s, j, j_z, что недопустимо. Поэтому j = 0, 2.
Поясним сказанное. В таблице представлены возможные значения суммарной проекции полного момента j двух фермионов с j₁ = j₂ = ³/₂ на ось Z, то есть значения j_z = ( j₁ )_z + ( j₂ )_z.

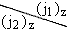	-3/2	-1/2	1/2	3/2
-3/2	-3	-2	-1
-1/2	-2	-1
1/2	-1
3/2

Если фермионы тождественны, то они не могут иметь одинаковые наборы n, l, j, j_z. Поэтому необходимо исключить все наборы j_z = ( j₁ )_z + ( j₂ )_z, находящиеся на диагонали таблицы. Кроме того, два состояния, различающиеся обменом ( j₁ )_z и ( j₂ )_z, являются одним и тем же состоянием. Поэтому можно исключить j_z, находящиеся ниже диагонали. Итак, приходим к следующей таблице

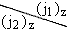	-3/2	-1/2	1/2	3/2
-3/2		-2	-1
-1/2
1/2
3/2

Набор j_z = -2, -1, 0, 1, 2 соответствует j = 2. Оставшееся значение j_z = 0 соответствует j = 0. Таким образом, для тождественных фермионов остаются j = 0 и 2.

2. Сравнив экспериментально измеренное значение магнитного момента дейтрона 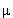=0.86 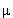_N с магнитным моментом системы нейтрон-протон в состоянии с j = 1 и относительным орбитальным моментом L = 0 (S₁-состояние), оценить вклад компоненты с j = 1 и L = 2 (D₁-состояние) в волновую функцию дейтрона.