Комплексная форма ряда Фурье

Спектральное разложение периодического сигнала можно выполнить, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:

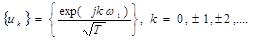
Легко видеть, что функции этой системы периодичны с периодом Т и ортонормированы на отрезке времени [—Т/2, Т/2], так как

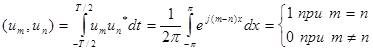
Ряд Фурье произвольного периодического сигнала в дан­ном случае принимает вид

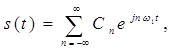(1)

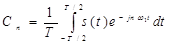
Выражение (1) представляет собой ряд Фурье в комплекс­ной форме.

Спектральный анализ непер-х сигналов. Преобразование Фурье. Понятие спектральной плотности. Обратное преобразование Фурье. Условие существования спектральной плотности сигнала. Спектральная плотность прямоугольного видеоимпульса. Спектральная плотность дельта функции. Связь между длительностью импульса и шириной его спектра.

Дан s (t) - одиночный импульсный сигнал конечной длительности. Дополняем его такими же сигналами, периодически следую­щими через некоторый интервал времени T, получим периодическую последовательность S_пер (t), которая может быть представлена в виде комплексного ряда Фурье 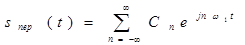(1)

с коэффициентами 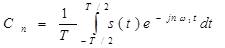(2)

Для того чтобы вернуться к одиночному импульсному сигналу, устремим к бесконечности период повторения Т. При этом, очевидно:

1. Частоты соседних гармоник nω₁ и (n + l)ω₁ окажутся сколь угодно близкими, так что в формулах (1) и (2) дискретную переменную nω₁ можно заменить непрерывной переменной ω — текущей частотой.

2. Амплитудные коэффициенты С_n станут неограниченными малыми из-за наличия величины Т в знаменателе формулы (2).

Задача состоит в нахождении предельного вида формулы (1) при T→∞.

Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары. Каждой такой паре отвечает гармоническое колебание с комплексной амплитудой 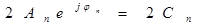(3)

Рассмотрим малый интервал частот Δω, образующий окрестность некоторого выбранного значения частоты ω₀. В пределах этого интервала будет содержаться N=Δω/ω₁=ΔωT/(2π) отдельных пар спектральных составляющих, частоты которых отличаются мало.Поэтому составляющие можно складывать так, как будто все они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами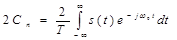

В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала Δω:

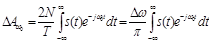. (4)

Функция 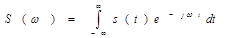(5)

носит название спектральной плотности сигнала s (t). Формула (5) осуществляет преобразование Фурье данного сигнала.

Решим обратную задачу спектральной теории сигналов: найдем сигнал по его спектральной плотности, которую будем считать заданной.

.

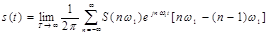Поскольку в пределе частотные интервалы между соседними гармониками неограниченно сокращаются, последнюю сумму следует заменить интегралом 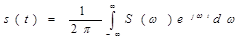Эта важная формула называется обратным преобразованием Фурье для сигнала s(t).

Сформулируем окончательно фундаментальный результат: сигнал s(t) и его спектральная плотность S(ω) взаимно однозначно связаны прямым и обратным преобразованиями Фурье^

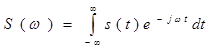
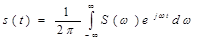
Спектральное представление сигналов открывает прямой путь к анализу прохождения сигналов через широкий класс радиотехнических цепей, устройств и систем. Сигналу s(t) можно сопоставить его спектральную плотность s(ω) в том случае, если этот сигнал абсолютно интегрируем, т. е. существует интеграл .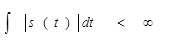

Подобное условие значительно сужает класс допустимых сигналов. Так, в указанном классическом смысле невозможно говорить о спектральной плотности гармонического сигнала и (t) =U_mcosω₀t , существующего на всей бесконечной оси времени.

Спектральная плотность прямоугольного видеоимпульса.

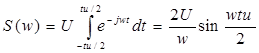
Спектральная плотность этого сигнала есть вещественная функция частоты. Удобно ввести безразмерную переменную 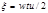и тогда 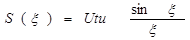Значение спектральной плотности на нулевой частоте равно площади импульса S(0)=Utu

Спектральная плотность дельта функции.

s(t) представ.короткий импульс имеющий площадь А и сосредоточенный в момент времени t=0.Математич. модель сигнала s(t)=Aδ(t).Спектральна плотность этого сигнала 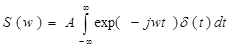. На основании фильтрующего свойства дельта функции входящий сигнал численно равен значению классической функции в точке, где сосредоточена обобщенная функция. Поэтому S(w)=A=const.Дельта импульс имеет равномерный спектр на всех частотах